Understanding Functions A function is a rule or

Understanding Functions

A function is a rule or a correspondence that associates each x-value with exactly one y-value. The set of all the x-values is called the Domain of the function. For each element x in the domain, the corresponding element y is called the image of x. The set of all images of the elements of the domain is called the Range of the function.

4 ways to describe a function Mapping Diagram Ordered pairs/Table of values Graph Rule (equation)

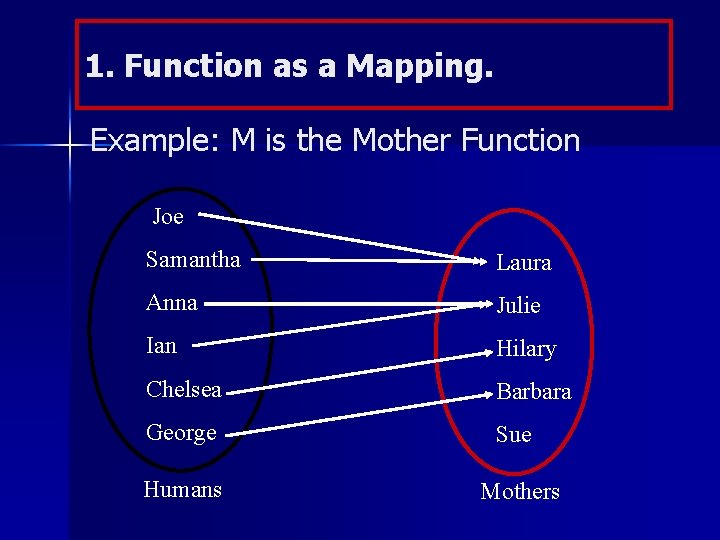
1. Function as a Mapping. Example: M is the Mother Function Joe Samantha Laura Anna Julie Ian Hilary Chelsea Barbara George Sue Humans Mothers

M: Mother function Domain of M {Joe, Samantha, Anna, Ian, Chelsea, George} Range of M {Laura, Julie, Hilary, Barbara} In function notation we can write: M(Anna) = Julie or M(George) = Barbara Also, if we are told M(x) = Hilary, That means that x must be = Chelsea

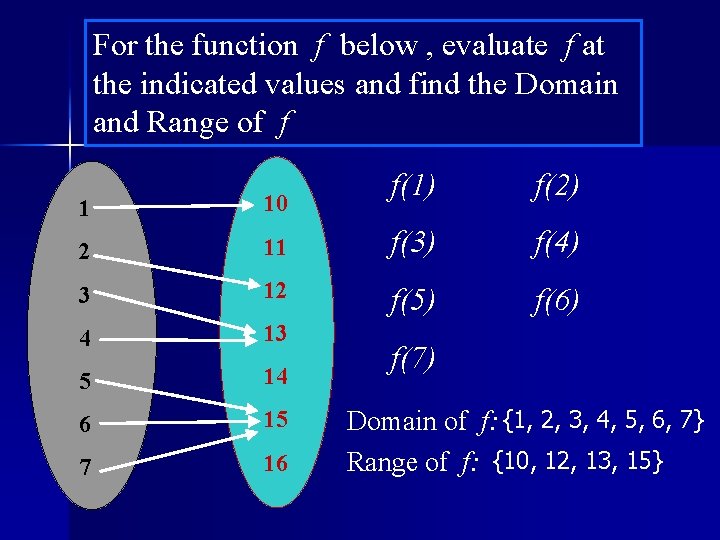
For the function f below , evaluate f at the indicated values and find the Domain and Range of f f(1) f(2) 1 10 2 11 f(3) f(4) 3 12 f(5) f(6) 4 13 5 14 6 15 7 16 f(7) Domain of f: {1, 2, 3, 4, 5, 6, 7} Range of f: {10, 12, 13, 15}

2. Function as a Set of Ordered Pairs A function is a set of ordered pairs with the property that no two ordered pairs have the same first component and different second components. In other words, you can’t have two different y-values for the same x-value.

For each x, there is one related y-value h: {(-2, 3), (1, 3), (4, 5), (10, 5)} j: {(1, -2), (2, 2), (3, 1), (4, -2)} p: {(0, 0), (1, 1)} What is h(1)? What is j(1)? What is p(1)? For what values is h(x) = 5?

The mother function M can also be written as ordered pairs M = {(Joe, Laura), (Samantha, Laura), (Anna, Julie), (Ian, Julie), (Chelsea, Hillary), (George, Barbara) }

3. Function as a Graph Another way to depict a function, is to display the ordered pairs on a graph on the coordinate plane, with the x-values along the horizontal axis, and the y-values on the vertical axis.

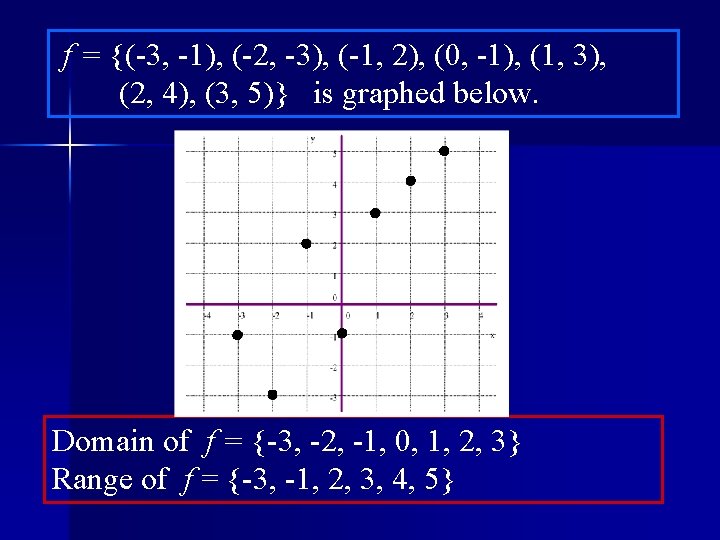
f = {(-3, -1), (-2, -3), (-1, 2), (0, -1), (1, 3), (2, 4), (3, 5)} is graphed below. Domain of f = {-3, -2, -1, 0, 1, 2, 3} Range of f = {-3, -1, 2, 3, 4, 5}

4. Function Defined by a Rule Let f be a function, consisting of ordered pairs where the second element of the ordered pair is the square of the first element. Some of the ordered pairs in f are (1, 1) (2, 4), (3, 9), (4, 16), ……. f is best defined by the rule f(x) = x²

Function Notation f(x) Functions defined on infinite sets are denoted by algebraic rules. Examples of functions defined on all Real numbers f(x) = x² g(x) = 2 x – 1 h(x) = x³ The symbol f(x) represents the y-value in the Range corresponding to the Domain value x. The point (x, f(x)) belongs to the function f.

Evaluating functions Determine the function values (y-values) for the given x-values. 5 -7. 5 2 -1 5 Undefined -11 Undefined 3 If x is in the denominator, or in a square root, there will be restrictions on the Domain.

Graph of a function The graph of the function f(x) is the set of points (x, y) in the plane that satisfies the relation y = f(x). E. g. : The graph of the function f(x) = 2 x – 1 is the graph of the equation y = 2 x – 1, which is a line. Each point on the line is (x, f(x))

Domain and Range from a Graph Remember: Domain is the set of all x-values. On a graph, it is represented by all the values from left to right. Range is the set of all the y-values. On a graph, it is represented by all the values from bottom to top. For Real numbers, we write the Domain and Range in interval notation. [ #, # ]

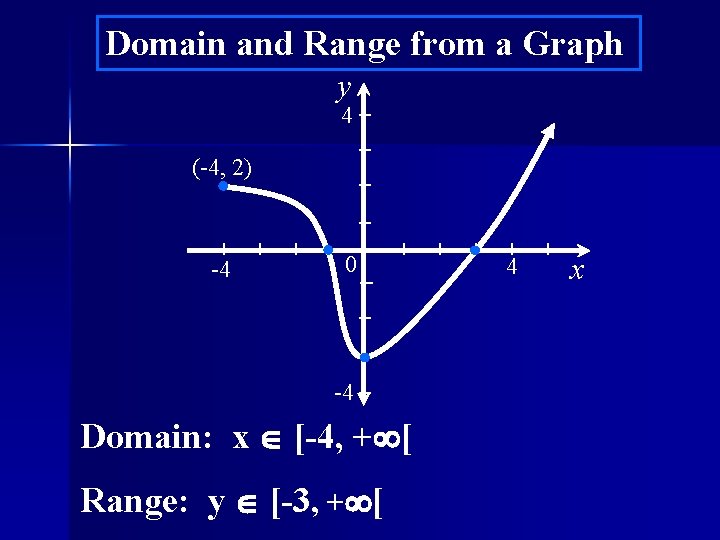
Domain and Range from a Graph y 4 (-4, 2) -4 0 -4 Domain: x [-4, + [ Range: y [-3, + [ 4 x

The Zero of a Function The zero of a function is the place where the function hits the x-axis. It is the x-intercept. What is the zero of the function graphed at the right? y 2 -2 0 -2 2 x

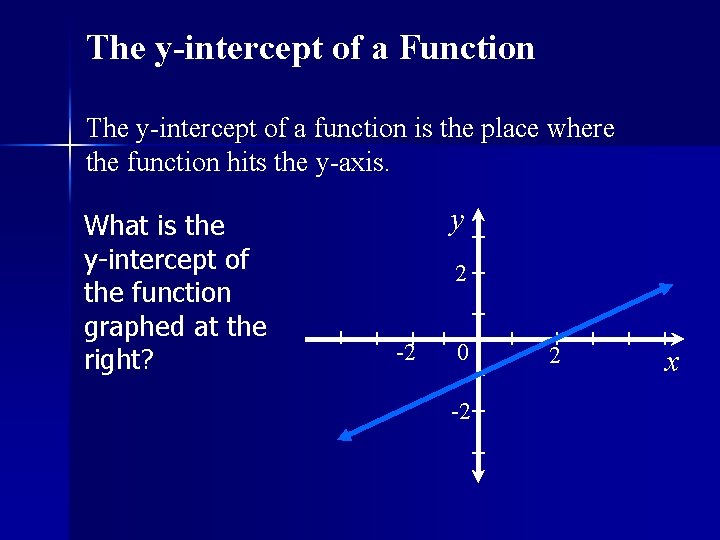
The y-intercept of a Function The y-intercept of a function is the place where the function hits the y-axis. What is the y-intercept of the function graphed at the right? y 2 -2 0 -2 2 x

Calculating the zero and y-intercept of a function. Calculate the zero of a function by making the function equal to zero and solving for x. Calculate the y-intercept by finding f(0). Given f(x) = 2 x + 10, find: a) the zero b) the y-intercept. f(x) = 2 x + 10 = 0 2 x = -10 x = -5 f(0) = 2(0) + 10 = 10 y = 10

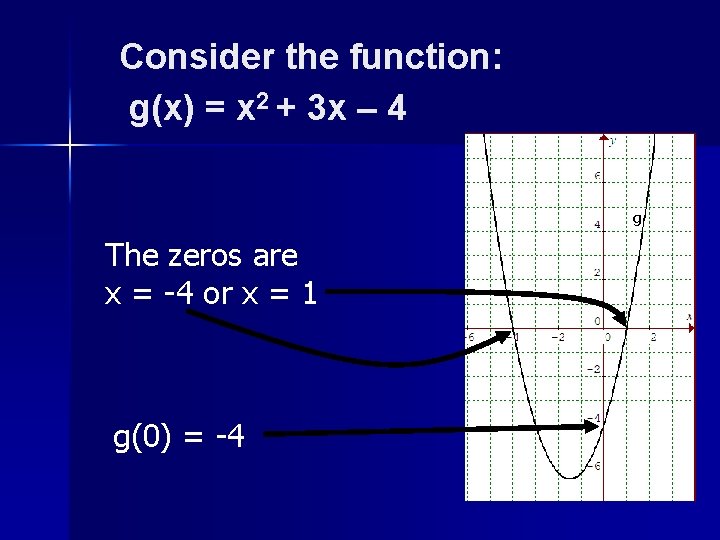
Consider the function: g(x) = x 2 + 3 x – 4 Calculate the y-intercept of g: g(0) = (0)2 + 3(0) – 4 = -4 Calculate the zeros of g: g(x) = x 2 + 3 x – 4 = 0 (x + 4)(x – 1) = 0 x = -4 or x = 1

Consider the function: g(x) = x 2 + 3 x – 4 g The zeros are x = -4 or x = 1 g(0) = -4

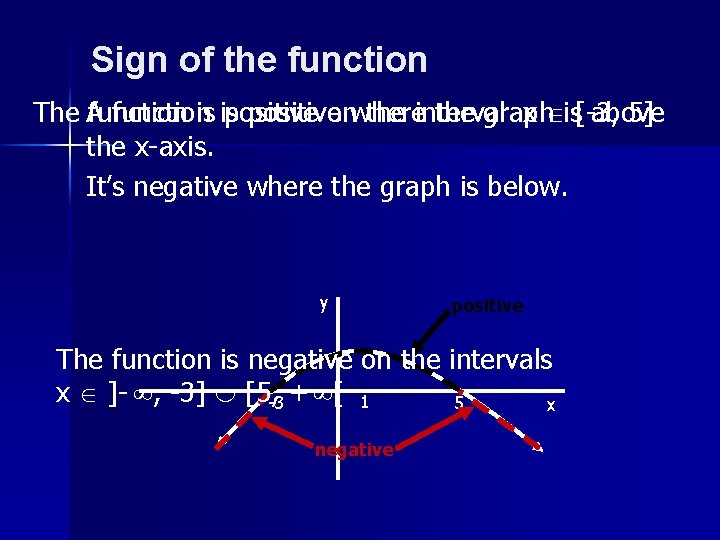
Sign of the function positive the graph above The A function is is positive onwhere the interval x is[-3, 5] the x-axis. It’s negative where the graph is below. y positive The function is negative on the intervals x ]- , -3] [5, -3 + [ 1 5 x negative

Intervals of Increase or Decrease We need to identify where the function is increasing or decreasing y -3 Increasing: x ]- , 1] 1 5 x Decreasing: x [1, + [

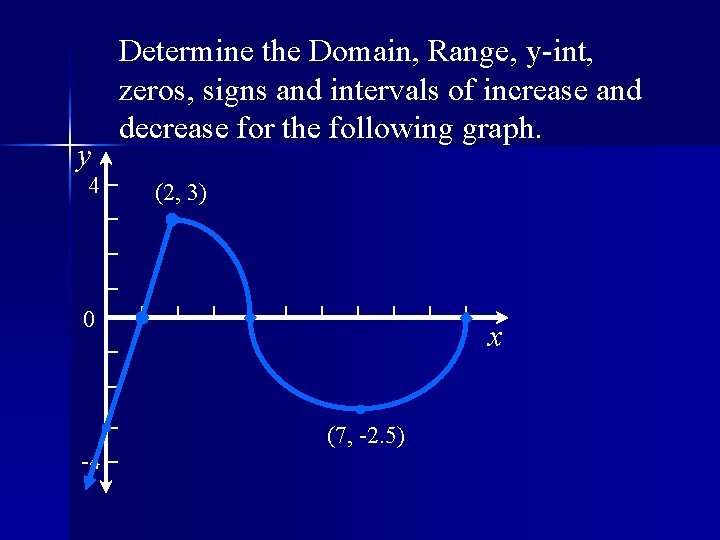
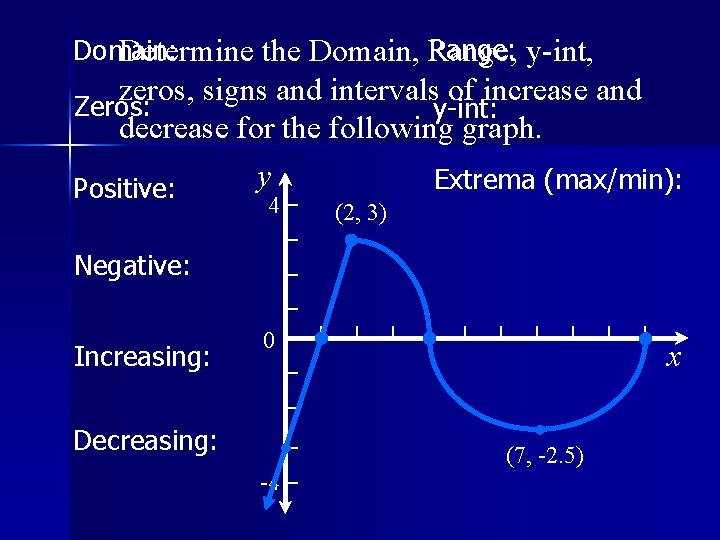
y 4 Determine the Domain, Range, y-int, zeros, signs and intervals of increase and decrease for the following graph. (2, 3) 0 -4 x (7, -2. 5)

Range: y-int, Domain: Determine the Domain, Range, zeros, signs and intervals of increase and Zeros: y-int: decrease for the following graph. y Extrema (max/min): Positive: 4 (2, 3) Negative: Increasing: 0 Decreasing: -4 x (7, -2. 5)

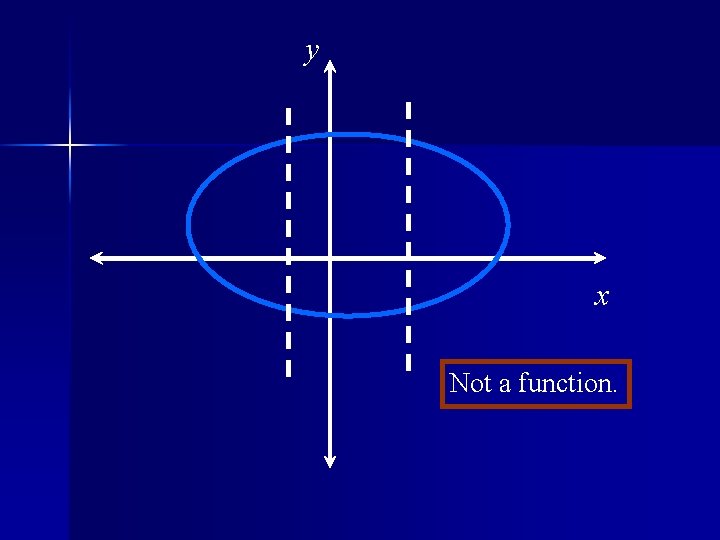
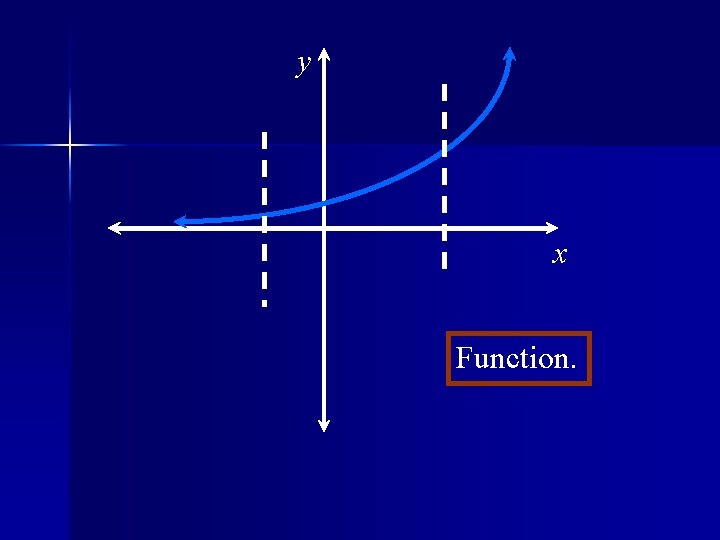
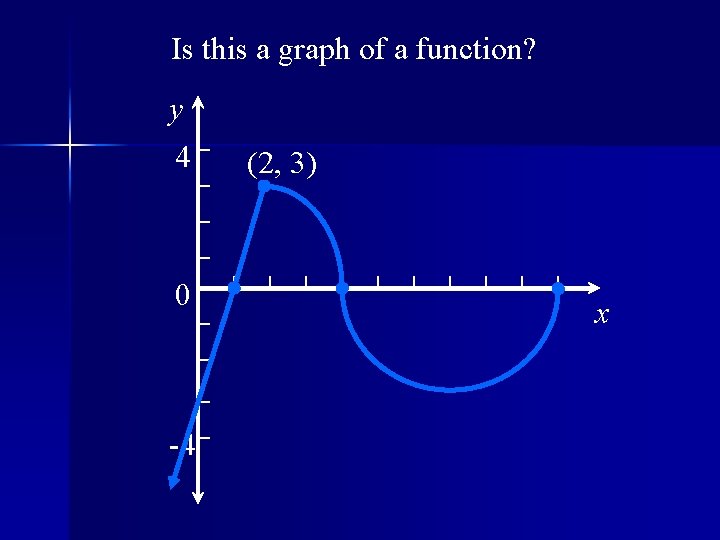
Theorem Vertical Line Test A set of points in the xy - plane is the graph of a function if and only if a vertical line intersects the graph in at most one point.

y x Not a function.

y x Function.

Is this a graph of a function? y 4 0 -4 (2, 3) x