Understanding discharge formation in GEM detectors by simulating

Understanding discharge formation in GEM detectors by simulating the primary charge density P. Gasik, AM, L. Fabbietti, J. Margutti, NIM A 870 (2017) 116. Andi Mathis Technische Universität München 19. 06. 2018 RD 51 Collaboration Meeting

Discharges in GEMs • Breakdown appears when the total charge in the avalanche reaches critical value Qmax – Qmax = Gmax × nprim ≈ 107 e– Beware of highly ionizing particles! – “High rate behavior and discharge limits in micro-pattern detectors”, A. Bressan et al. NIM A 424 (1999) 321 • Spark in GEM: – ΔVGEM 0 – may be harmful to the detector and electronics (large energy release) Q~10 7 Q~10 9 8 S. Bachmann et al, NIM A 479 (2002) 294 19 June 2018 • Multi-GEM structures charge spreads over many GEM holes • Dedicated workshop on Thursday Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 2

GEMs in harsh environment • COMPASS: Up to 1 MHz/cm 2 in the middle segments • LHCb: Up to 0. 5 MHz/cm 2 in the middle segments • TOTEM: Operated at 10 k. Hz/cm 2 in the middle • Trackers – Short drift gap O(mm), Ar-based mixtures – No pile-up expected – Up to a few electrons/hole expected (MIP) • Troublemakers – Highly Ionizing fragments (Nprim, α = 104 × Nprim, MIP) – Charge densities in the bottom GEM, after full amplification (e. g. IBF-optimized multi-GEM stacks) • Stability of your system relies on the stability of a single GEM! – Critical charge density & Influence of the gas? 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 3

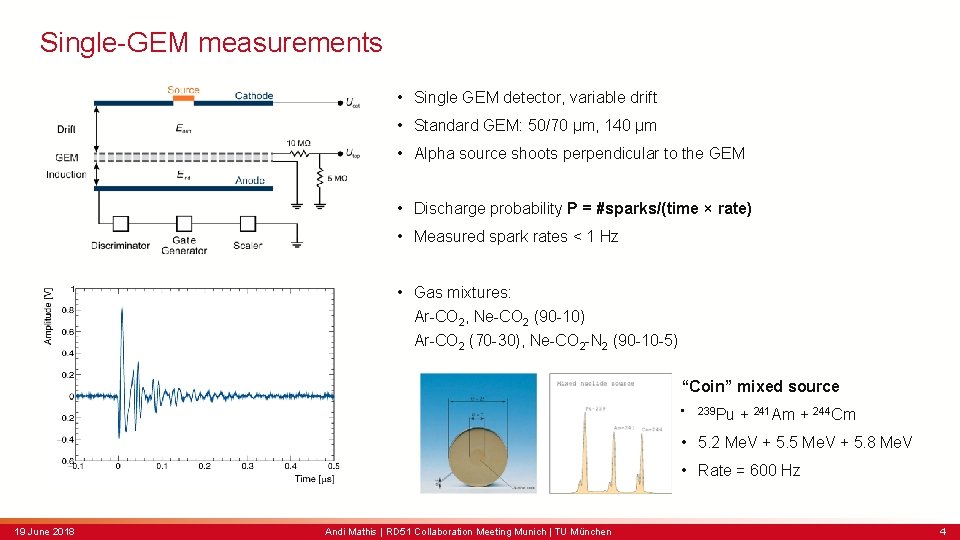
Single-GEM measurements • Single GEM detector, variable drift • Standard GEM: 50/70 µm, 140 µm • Alpha source shoots perpendicular to the GEM • Discharge probability P = #sparks/(time × rate) • Measured spark rates < 1 Hz • Gas mixtures: Ar-CO 2, Ne-CO 2 (90 -10) Ar-CO 2 (70 -30), Ne-CO 2 -N 2 (90 -10 -5) “Coin” mixed source • 239 Pu + 241 Am + 244 Cm • 5. 2 Me. V + 5. 5 Me. V + 5. 8 Me. V • Rate = 600 Hz 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 4

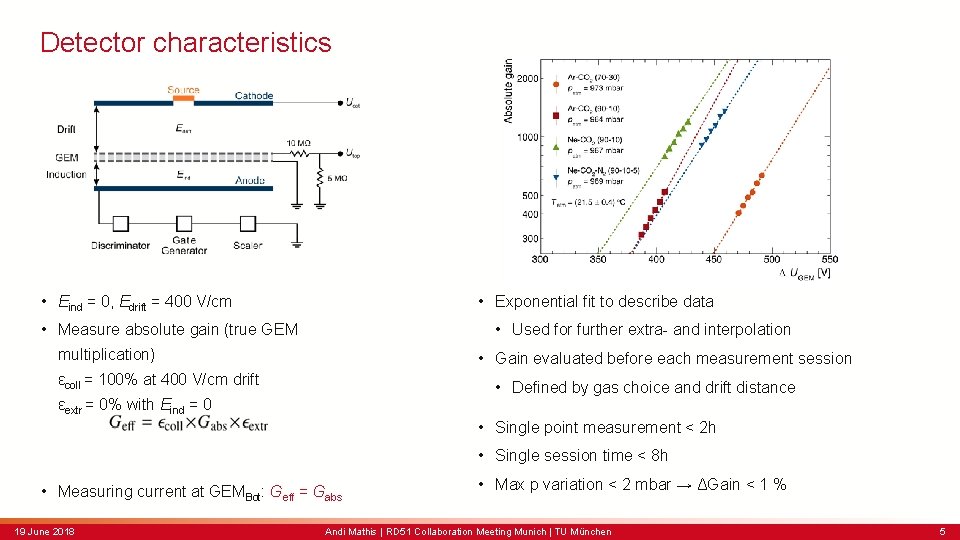
Detector characteristics • Exponential fit to describe data • Eind = 0, Edrift = 400 V/cm • Used for further extra- and interpolation • Measure absolute gain (true GEM multiplication) • Gain evaluated before each measurement session εcoll = 100% at 400 V/cm drift • Defined by gas choice and drift distance εextr = 0% with Eind = 0 • Single point measurement < 2 h • Single session time < 8 h • Measuring current at GEMBot: Geff = Gabs 19 June 2018 • Max p variation < 2 mbar → ΔGain < 1 % Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 5

Discharge studies – charge density hypothesis Ar-CO 2, G= 30, 000 Ne-CO 2 -N 2, G= 45, 000 • Discharge probability strongly depends on inclination angle and amount of ionization close to the GEM 3 GEM – Shooting perpendicular increases discharge rate by ~ one order of magnitude P ~ 10 -6 P ~ 10 -5 19 June 2018 GEANT 4 sim Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 6

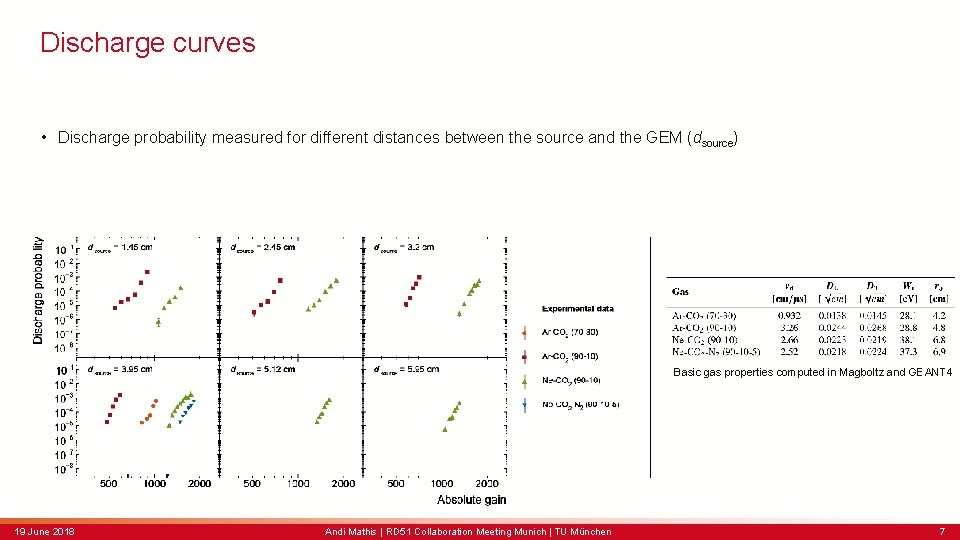
Discharge curves • Discharge probability measured for different distances between the source and the GEM (dsource) Basic gas properties computed in Magboltz and GEANT 4 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 7

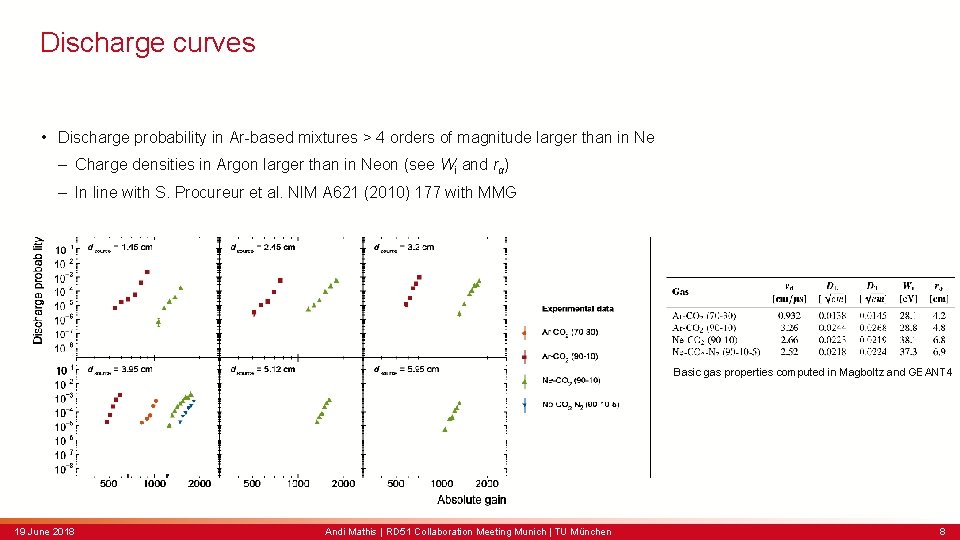
Discharge curves • Discharge probability in Ar-based mixtures > 4 orders of magnitude larger than in Ne – Charge densities in Argon larger than in Neon (see Wi and rα) – In line with S. Procureur et al. NIM A 621 (2010) 177 with MMG Basic gas properties computed in Magboltz and GEANT 4 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 8

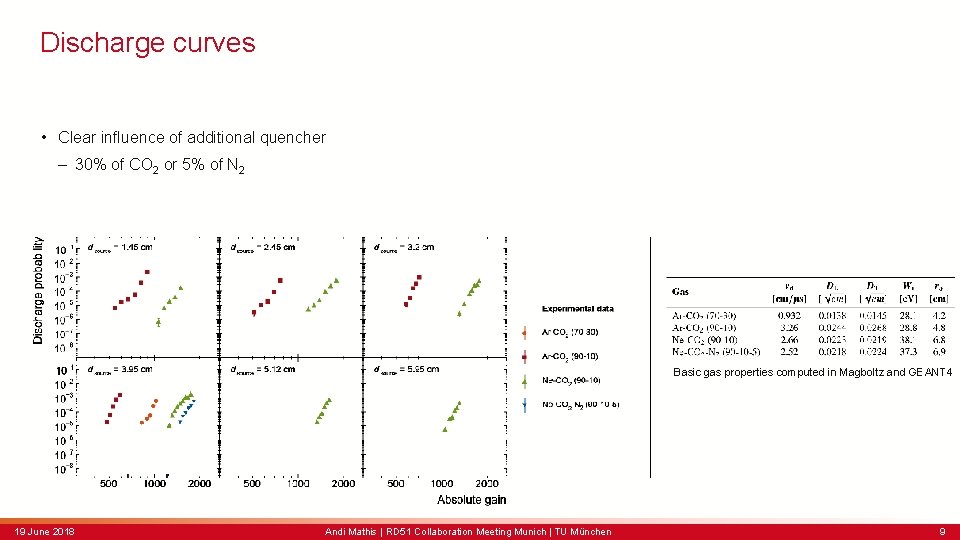
Discharge curves • Clear influence of additional quencher – 30% of CO 2 or 5% of N 2 Basic gas properties computed in Magboltz and GEANT 4 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 9

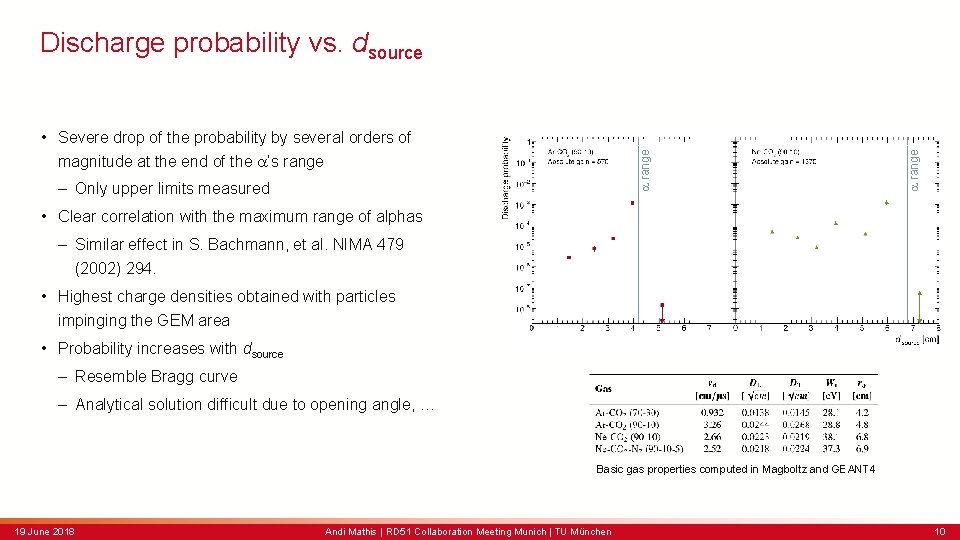
a range • Severe drop of the probability by several orders of magnitude at the end of the a’s range – Only upper limits measured a range Discharge probability vs. dsource • Clear correlation with the maximum range of alphas – Similar effect in S. Bachmann, et al. NIMA 479 (2002) 294. • Highest charge densities obtained with particles impinging the GEM area • Probability increases with dsource – Resemble Bragg curve – Analytical solution difficult due to opening angle, … Basic gas properties computed in Magboltz and GEANT 4 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 10

Model source • Realistic model of the detector • Simulation of the energy deposit of alpha particles in the active detector medium (GEANT 4) • Conversion of energy deposit into ionization electrons nele = Edep/Wi • Drift of the electrons towards the GEM plane taking into account transverse and longitudinal diffusion and the electron drift velocity at Edrift = 400 V/cm – Smearing with Gaussian distribution – Repeated for many different dsource • Similar approach as in S. Procureur et al. NIM A 621 (2010) 177 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 11

Model source • Collection the charges according to their arrival position – Honeycomb pattern around the GEM holes – Assume 100 % collection efficiency t 2 t 1 • Multiplication of the charges inside the GEM holes – Count the electrons contained in single GEM holes • Critical limit for charges Qcrit in single GEM hole – When exceeded → discharge (à la Raether limit) • Count such large primary ionization clusters and normalize to the number of all α-particles – Discharge probability • Not known: Qcrit & the time it takes to develop a discharge tint – Parameter scan + χ2 minimization 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 12

Model source • Collection the charges according to their arrival position – Honeycomb pattern around the GEM holes – Assume 100 % collection efficiency t 2 t 1 • Multiplication of the charges inside the GEM holes – Count the electrons contained in single GEM holes • Critical limit for charges Qcrit in single GEM hole – When exceeded → discharge (à la Raether limit) Qcrit (exemplary) • Count such large primary ionization clusters and normalize to the number of all α-particles – Discharge probability • Not known: Qcrit & the time it takes to develop a discharge tint Max. number of electrons per GEM hole / Multiplication 19 June 2018 – Parameter scan + χ2 minimization Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 13

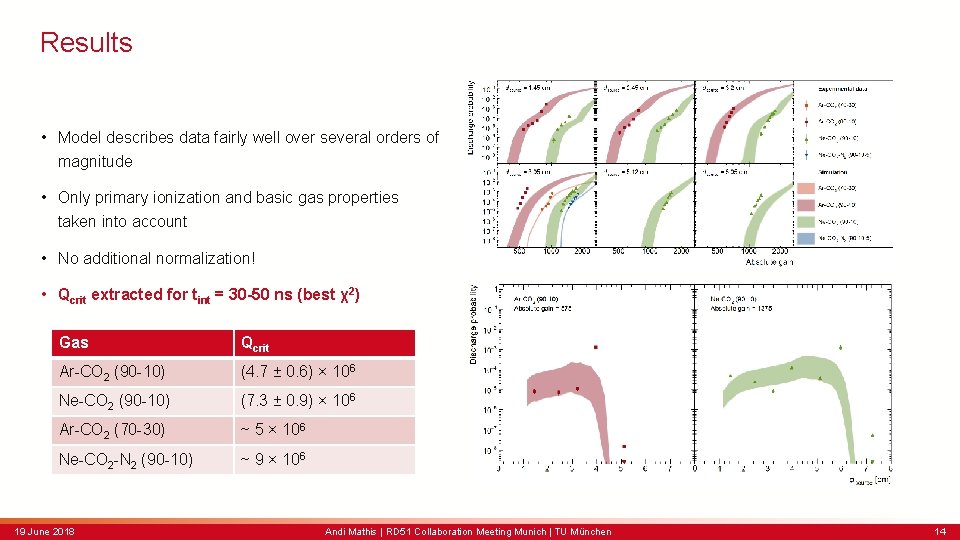
Results • Model describes data fairly well over several orders of magnitude • Only primary ionization and basic gas properties taken into account • No additional normalization! • Qcrit extracted for tint = 30 -50 ns (best χ2) Gas Qcrit Ar-CO 2 (90 -10) (4. 7 ± 0. 6) × 106 Ne-CO 2 (90 -10) (7. 3 ± 0. 9) × 106 Ar-CO 2 (70 -30) ~ 5 × 106 Ne-CO 2 -N 2 (90 -10) ~ 9 × 106 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 14

A few words on t. Int • What is the meaning of tint >> 1 ns? – Time needed to accumulate Qcrit charges in the GEM hole – Build up space charge needed for streamer formation – Too long for electrons… • tint ~ 50 ns compatible with ion drift time in GEM hole – 1 -2 mm integration gap above GEM • Compatible with S. Franchino et al. , Nuclear Science Symposium and Medical Imaging Conference, IEEE (2015) 1 S. Franchino, IEEE (2015) 1 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 15

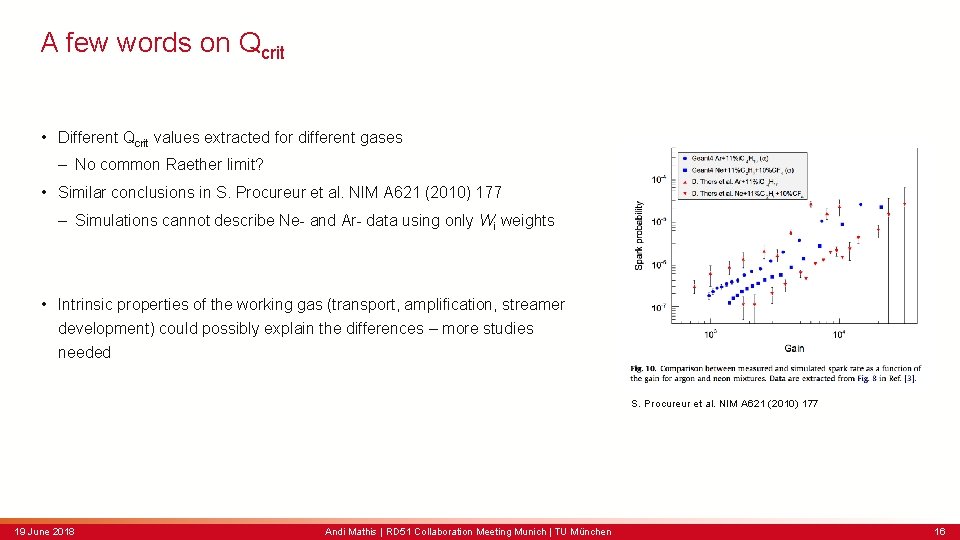
A few words on Qcrit • Different Qcrit values extracted for different gases – No common Raether limit? • Similar conclusions in S. Procureur et al. NIM A 621 (2010) 177 – Simulations cannot describe Ne- and Ar- data using only Wi weights • Intrinsic properties of the working gas (transport, amplification, streamer development) could possibly explain the differences – more studies needed S. Procureur et al. NIM A 621 (2010) 177 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 16

Summary • Discharge probability of a single GEM upon irradiation with alphas – Lower breakdown limits in Argon- than Neon-based mixtures – Observations consistent with the charge density hypothesis • Charge density model describes the data fairly well over several orders of magnitude – Qcrit = (5 – 9) × 106 electrons depending on the gas mixture • Estimated tint of ~50 ns point towards ion space-charge build-up in GEM hole prior to the discharge • Watch out particles impinging your detectors – the charge densities are the highest there! • Full text: P. Gasik, AM, L. Fabbietti, J. Margutti, NIM A 870 (2017) 116 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 17

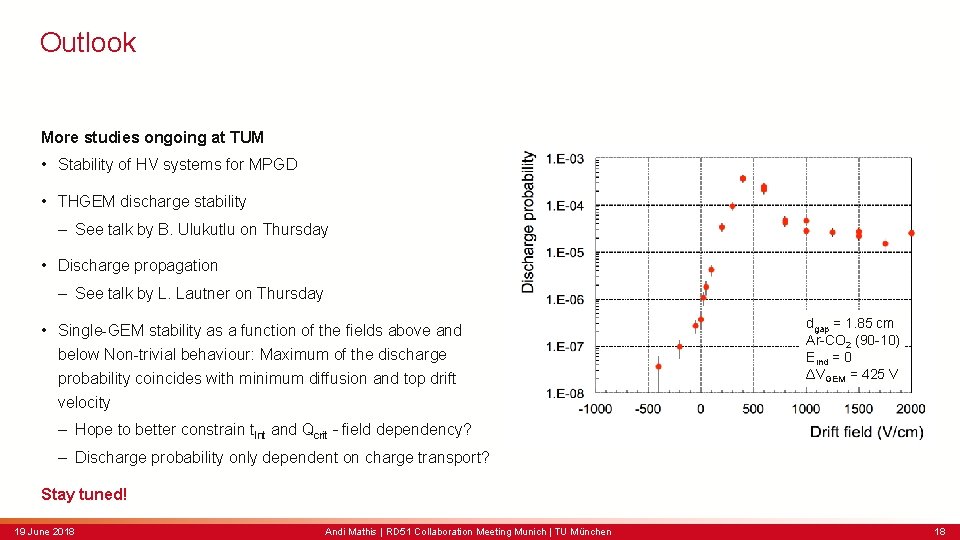
Outlook More studies ongoing at TUM • Stability of HV systems for MPGD • THGEM discharge stability – See talk by B. Ulukutlu on Thursday • Discharge propagation – See talk by L. Lautner on Thursday • Single-GEM stability as a function of the fields above and below Non-trivial behaviour: Maximum of the discharge probability coincides with minimum diffusion and top drift velocity dgap = 1. 85 cm Ar-CO 2 (90 -10) Eind = 0 ΔVGEM = 425 V – Hope to better constrain t. Int and Qcrit – field dependency? – Discharge probability only dependent on charge transport? Stay tuned! 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 18

Thank you very much!

Model Qcrit (exemplary) • Sorting into single GEM holes according to their arrival position – Honeycomb pattern around the GEM holes – Assume 100 % collection efficiency – Integrate over arrival time (tint) above a given GEM hole Max. number of electrons per GEM hole / Multiplication • Multiplication of the charges inside the GEM holes – Use absolute gain from the measurements – Count the electrons contained in single GEM holes • Critical limit for charges Qcrit in single GEM hole – When exceeded → discharge (a’la Raether limit) – Count such large primary ionisation clusters and normalize to the number of all α-particles • Discharge probability – Cut on discharge pile-up (one alpha – max one discharge) – Not known: Qcrit & tint → parameter scan + χ2 minimization 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 20

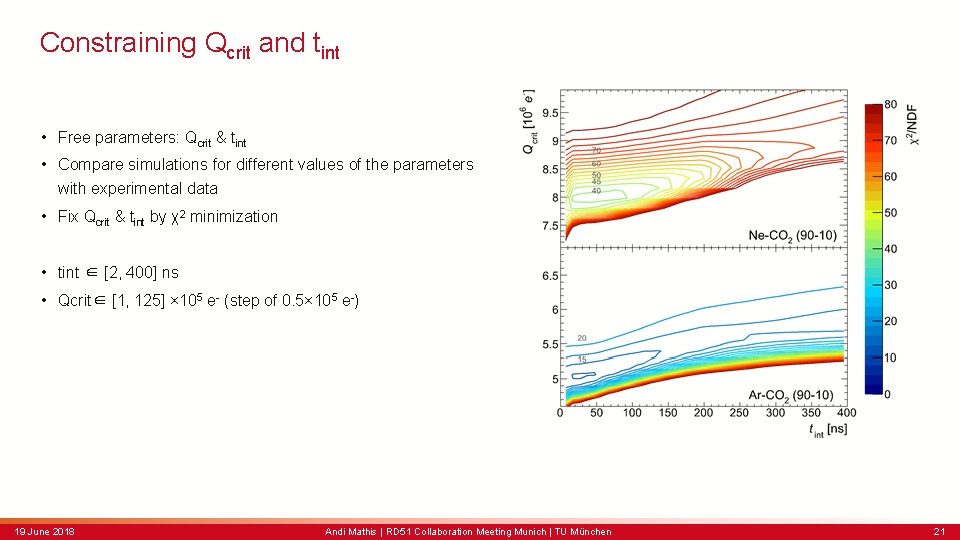
Constraining Qcrit and tint • Free parameters: Qcrit & tint • Compare simulations for different values of the parameters with experimental data • Fix Qcrit & tint by χ2 minimization • tint ∈ [2, 400] ns • Qcrit∈ [1, 125] × 105 e- (step of 0. 5× 105 e-) 19 June 2018 Andi Mathis | RD 51 Collaboration Meeting Munich | TU München 21