Understanding Deep learning from Fourier perspective The FPrinciple

Understanding Deep learning from Fourier perspective: The F-Principle Zhiqin Xu 许志钦 xuzhiqin@sjtu. edu. cn Shanghai Jiao Tong University 2020. 03. 08

1989 Single hidden layer can fit any function

Fitting is not enough!

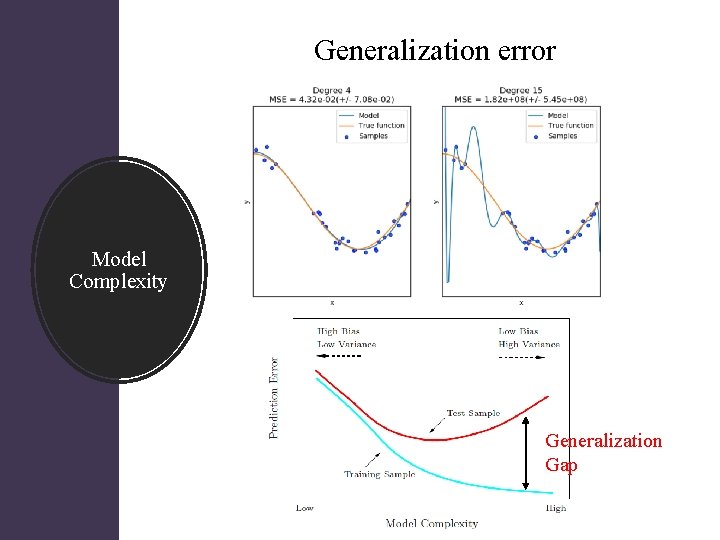
Generalization error Model Complexity Generalization Gap

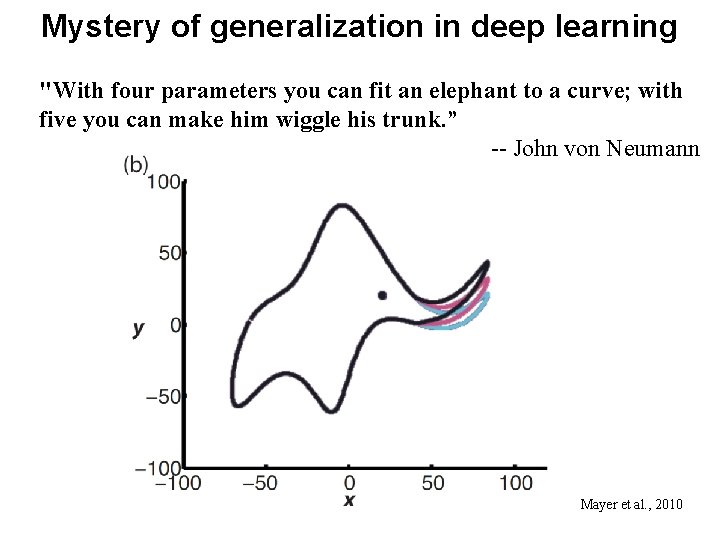
Mystery of generalization in deep learning "With four parameters you can fit an elephant to a curve; with five you can make him wiggle his trunk. ” -- John von Neumann Mayer et al. , 2010

model: millions of parameters five data points Overfitting? ?

DNN says: NO!

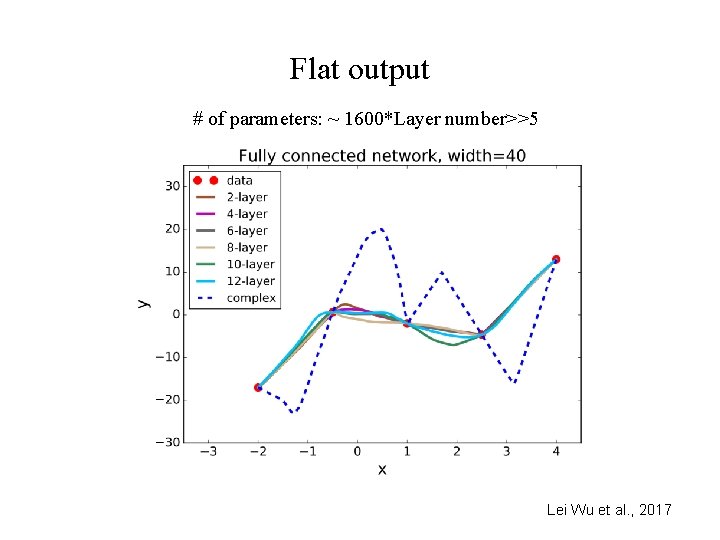
Flat output # of parameters: ~ 1600*Layer number>>5 Lei Wu et al. , 2017

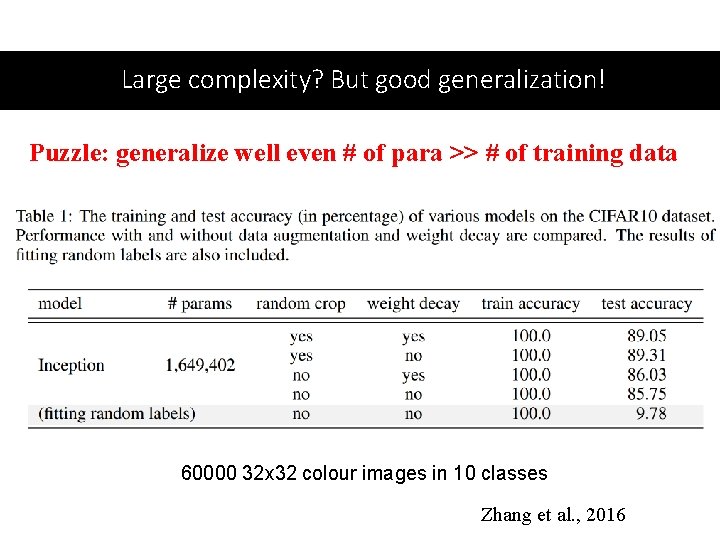
Large complexity? But good generalization! Puzzle: generalize well even # of para >> # of training data 60000 32 x 32 colour images in 10 classes Zhang et al. , 2016

Streetlight Effect A: I am looking for my quarter I dropped. B: Did you drop it here? A: No, I dropped it two blocks down the street. B: Then why are you looking for it here? A: Because the light is better here.

Modified Streetlight Effect A: I am looking for my quarter I dropped. B: Did you drop it here? A: No, I dropped it two blocks down the street. B: Then why are you looking for it here? A: Because I need to get familiar with the road structure first.

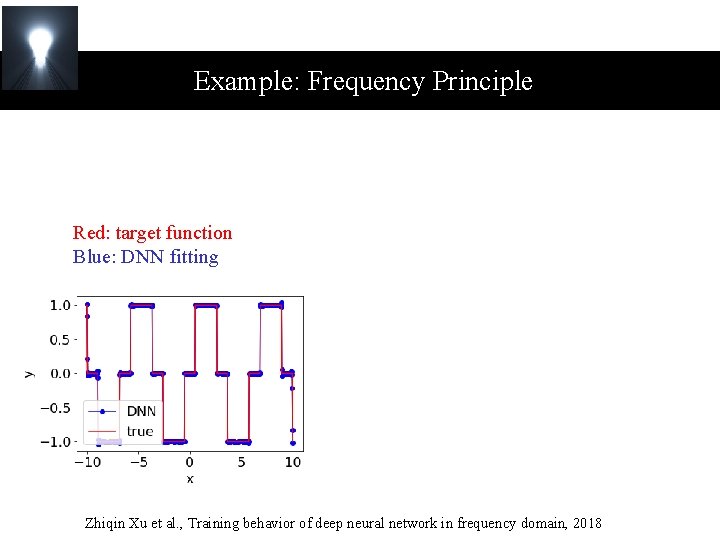
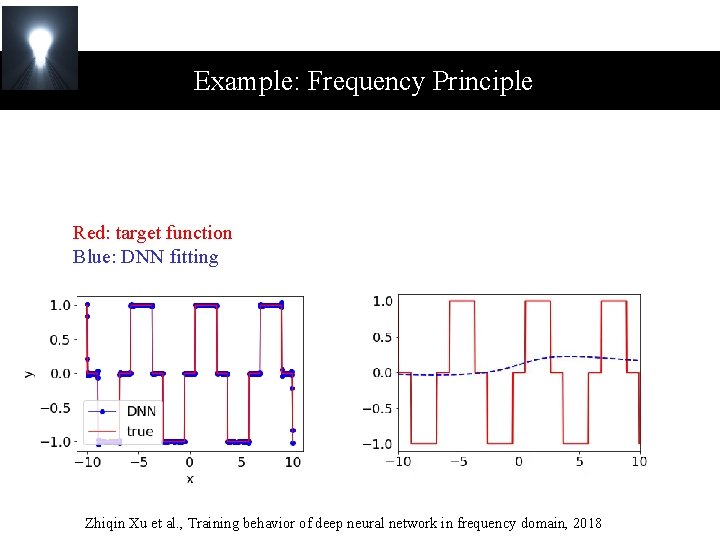
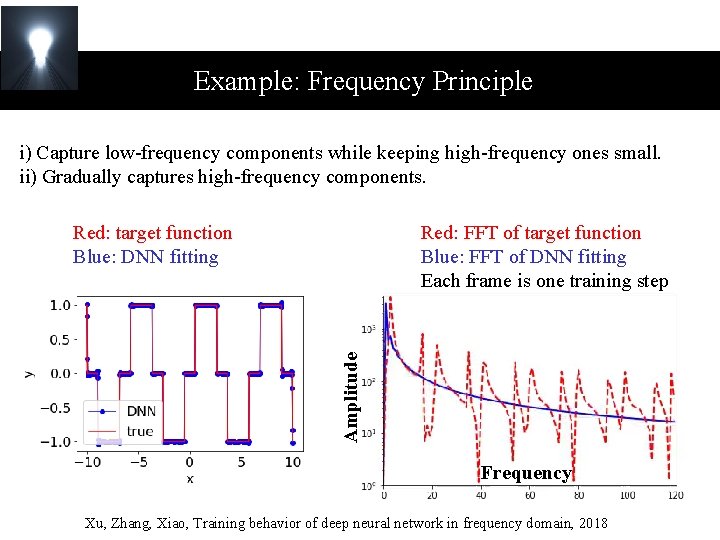
Example: Frequency Principle Red: target function Blue: DNN fitting Zhiqin Xu et al. , Training behavior of deep neural network in frequency domain, 2018

Example: Frequency Principle Red: target function Blue: DNN fitting Zhiqin Xu et al. , Training behavior of deep neural network in frequency domain, 2018

Motivation of frequency 平坦与振� �廓与��

Fourier transform

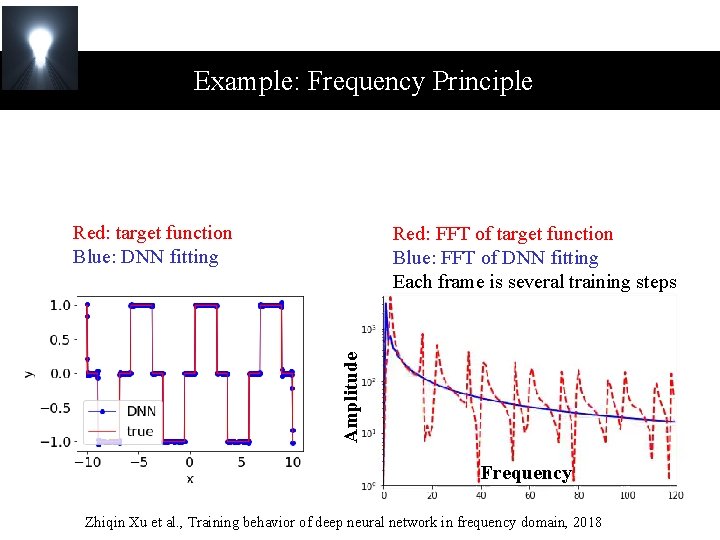
Example: Frequency Principle Red: target function Blue: DNN fitting Amplitude Red: FFT of target function Blue: FFT of DNN fitting Each frame is several training steps Frequency Zhiqin Xu et al. , Training behavior of deep neural network in frequency domain, 2018

Example: Frequency Principle i) Capture low-frequency components while keeping high-frequency ones small. ii) Gradually captures high-frequency components. Red: target function Blue: DNN fitting Amplitude Red: FFT of target function Blue: FFT of DNN fitting Each frame is one training step Frequency Xu, Zhang, Xiao, Training behavior of deep neural network in frequency domain, 2018

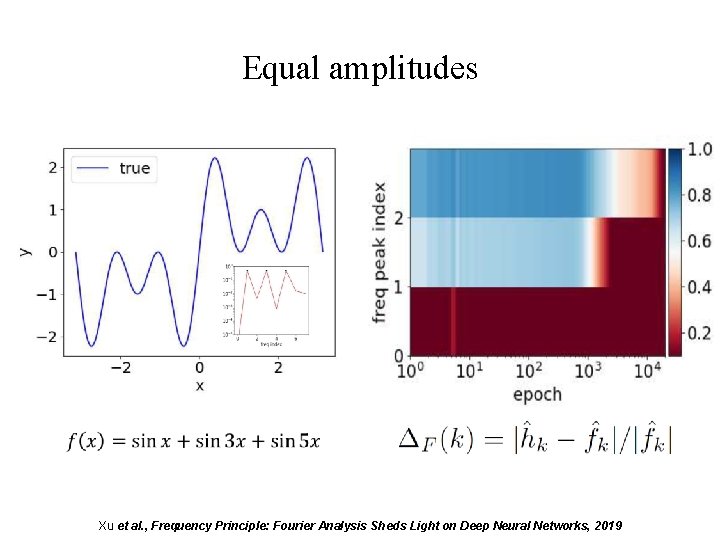
Equal amplitudes Xu et al. , Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, 2019

Modified Streetlight Effect A: I am looking for my quarter I dropped. B: Did you drop it here? A: No, I dropped it two blocks down the street. B: Then why are you looking for it here? A: Because I need to get familiar with the road structure first.

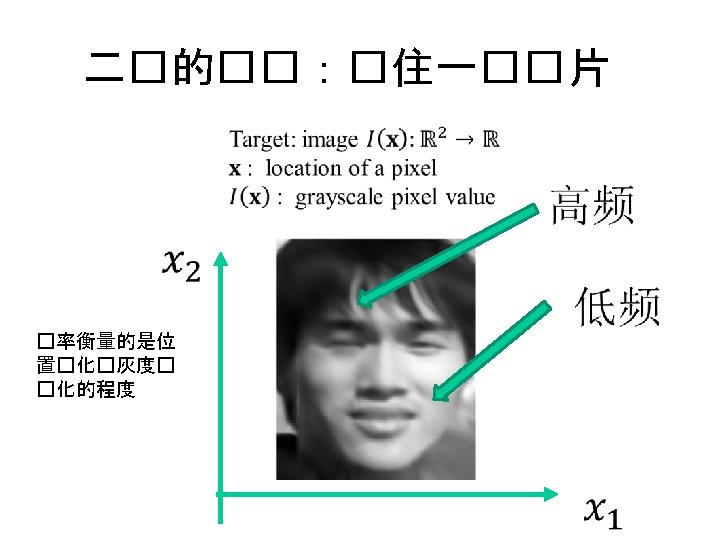
How DNN fits a 2 -d image?

F-Principle High-dimensional real data? Xu, Zhang, Luo, Xiao, Ma, Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, 2019

常�数据集 MNIST https: //blog. csdn. net/uytrrfg/article/details/83722860

常�数据集 CIFAR 10 The CIFAR-10 dataset consists of 60000 32 x 32 colour images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images. Canadian Institute for Advanced Research https: //www. cs. toronto. edu/~kriz/cifar. html

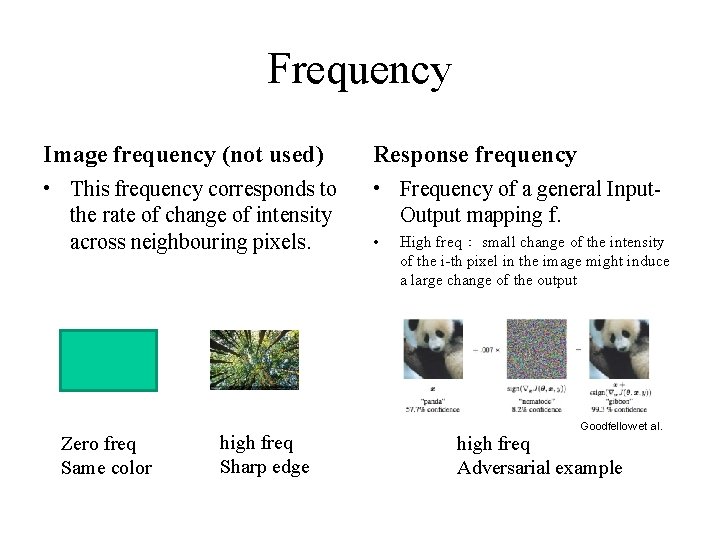
Frequency Image frequency (not used) Response frequency • This frequency corresponds to the rate of change of intensity across neighbouring pixels. • Frequency of a general Input. Output mapping f. Zero freq Same color high freq Sharp edge • High freq： small change of the intensity of the i-th pixel in the image might induce a large change of the output Goodfellow et al. high freq Adversarial example

Examining F-Principle for high dimensional real problems • �入和�出可以同�是高�的 MC 采� 逼近�分

Examining F-Principle for high dimensional real problems •

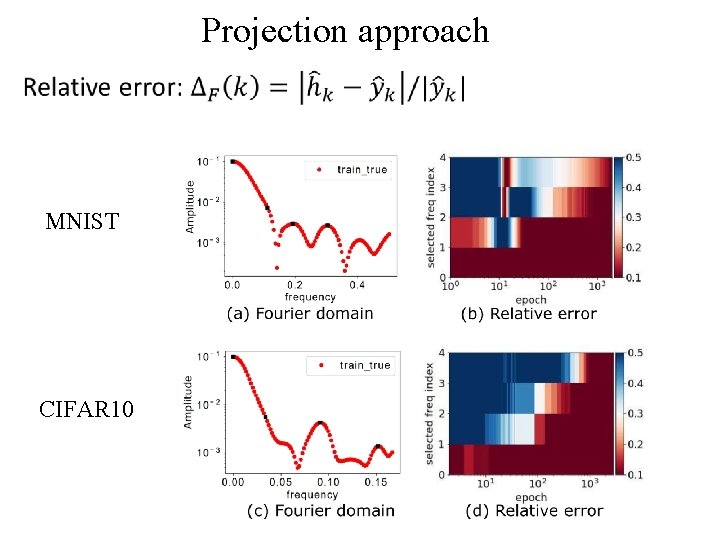
Projection approach •

Projection approach MNIST CIFAR 10

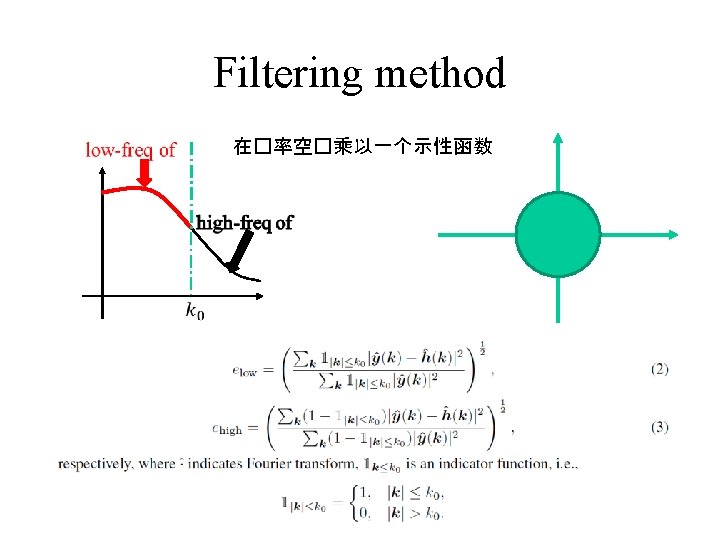
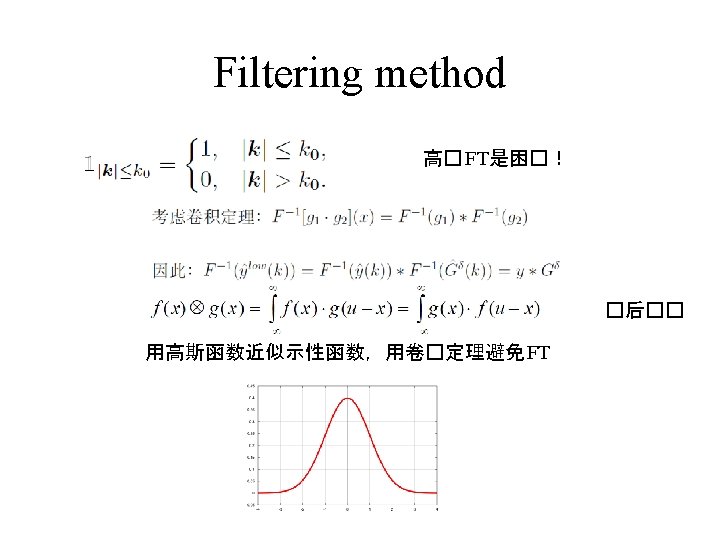
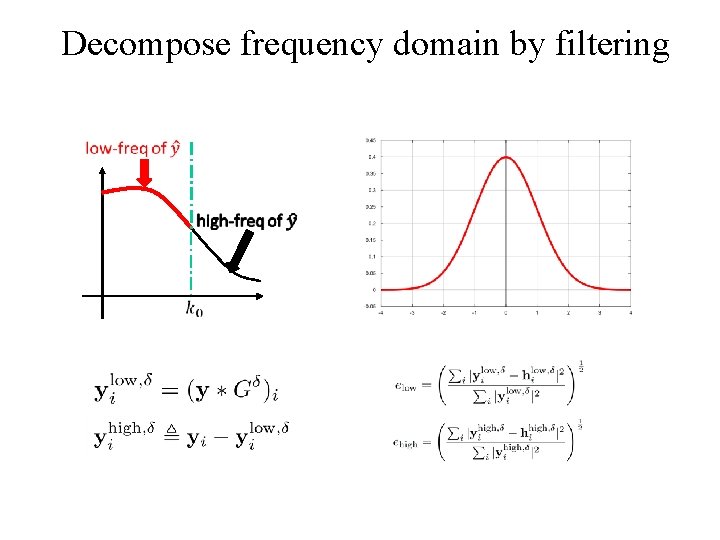
Decompose frequency domain by filtering

F-Principle in high-dim space MNIST CIFAR 10

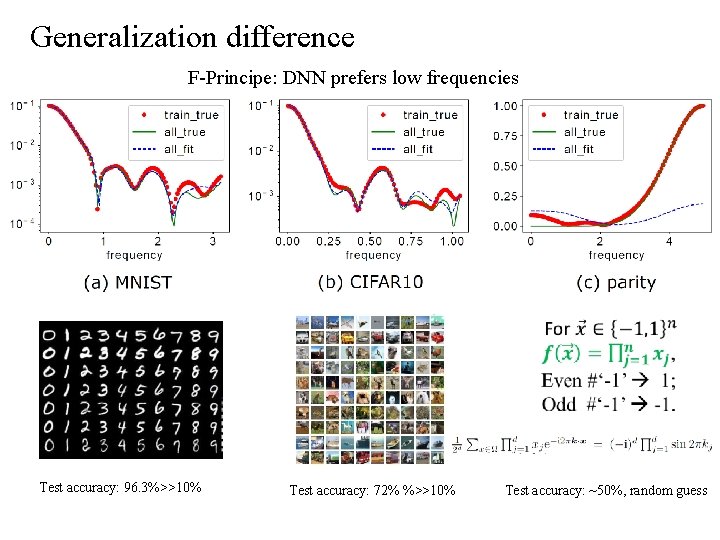
F-Principle DNN prefers low frequencies Generalization

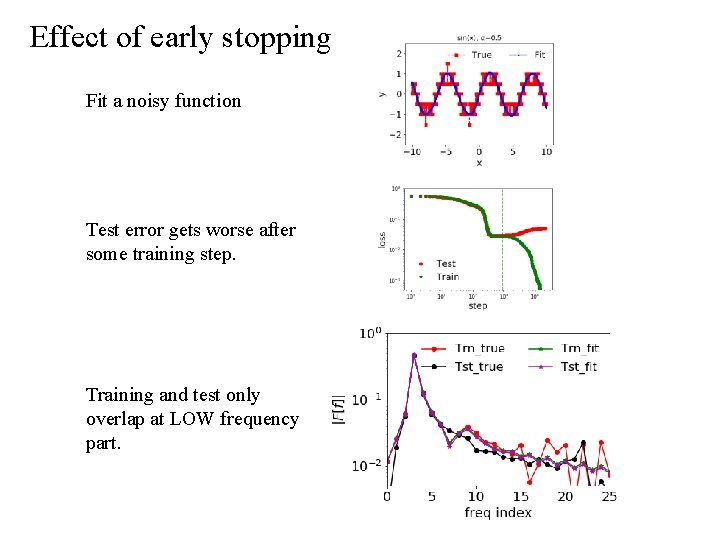
Effect of early stopping Fit a noisy function Test error gets worse after some training step. Training and test only overlap at LOW frequency part.

Generalization difference F-Principe: DNN prefers low frequencies Test accuracy: 96. 3%>>10% Test accuracy: 72% %>>10% Test accuracy: ~50%, random guess

Theory

Theory in a idealized setting

Analysis Low freq high freq

Xu, Zhang, Luo, Xiao, Ma, Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, 2019

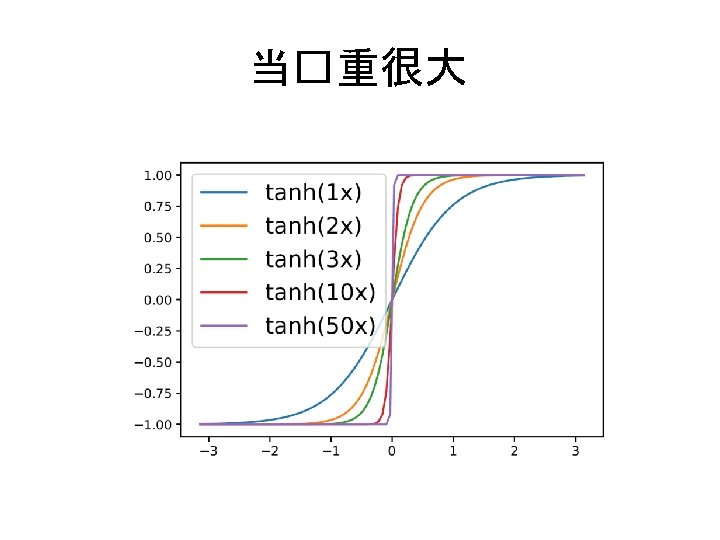
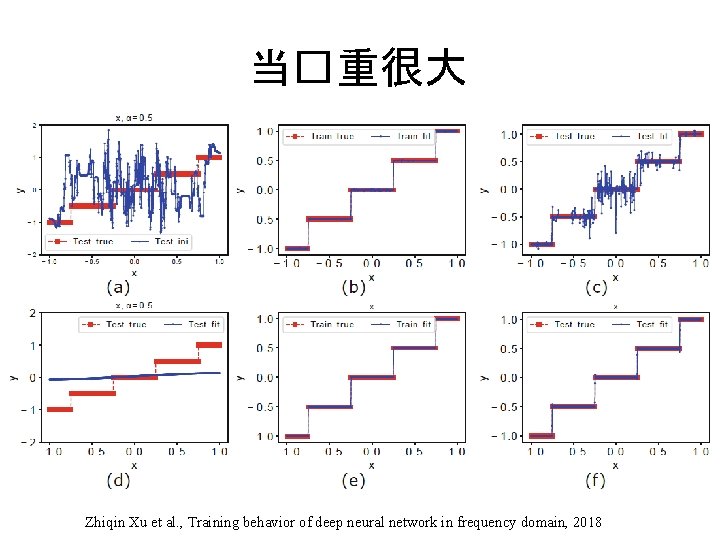
当�重很大 Zhiqin Xu et al. , Training behavior of deep neural network in frequency domain, 2018

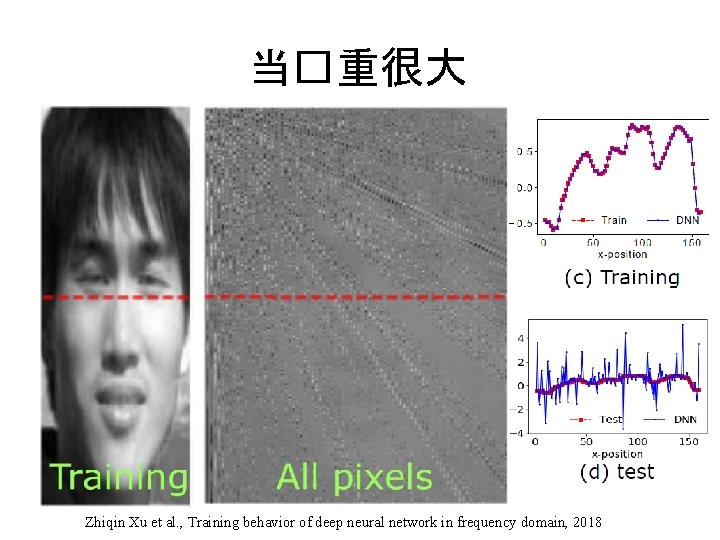
当�重很大 Zhiqin Xu et al. , Training behavior of deep neural network in frequency domain, 2018

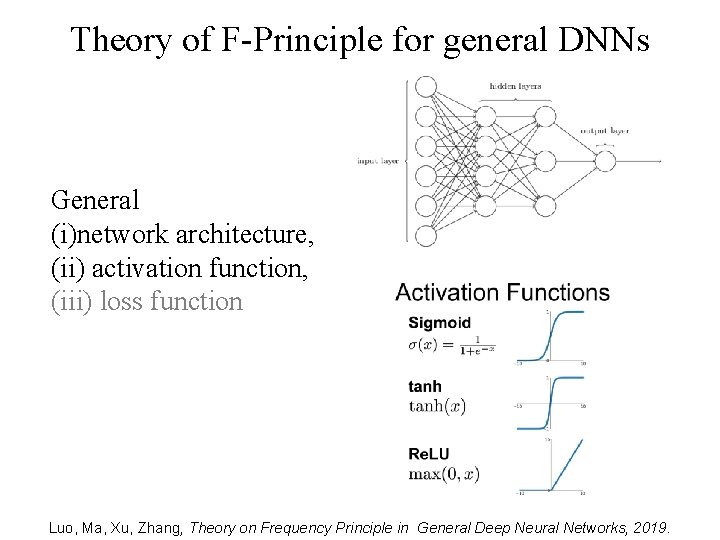
Theory of F-Principle for general DNNs General (i)network architecture, (ii) activation function, (iii) loss function Luo, Ma, Xu, Zhang, Theory on Frequency Principle in General Deep Neural Networks, 2019.

Conclusion Reference: DNNs prefer low frequencies! Joint work with Yaoyu Zhang, Tao Luo, Zheng Ma, Yanyang Xiao, Wei Cai (SMU) Acknowledge: Weinan E (Princeton), David W. Mc. Laughlin (CIMS) Xu*, Zhang, Luo, Xiao, Ma, Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, 201 9 *** Xu*, Zhang, Xiao, Training behavior of deep neural network in frequency domain, 2018 Xu*, Understanding training and generalization in deep learning by Fourier analysis, 2018 Zhang, Xu*, Luo, Ma, Explicitizing an Implicit Bias of the Frequency Principle in Two-layer Neural Networks, 2019 ** Zhang, Xu*, Luo, Ma, A type of generalization error induced by initialization in deep neural networks, 2019** Luo, Ma, Xu, Zhang, Theory on Frequency Principle in General Deep Neural Networks, 2019. Cai, Xu*, Multi-scale Deep Neural Networks for Solving High Dimensional PDEs, 2019. A summary note of the F-Principle can be found at my page https: //ins. sjtu. edu. cn/people/xuzhiqin/