Understanding constructive and destructive interference q In these



- Slides: 8

Understanding constructive and destructive interference q In these set of slides we will try to visualize how constructive and destructive interference take place (using the Bragg’s view of diffraction as ‘reflection’ from a set of planes). q It is easy to ‘see’ as to how constructive interference takes place; however, it is not that easy to see how ‘rays’ of the Bragg angle ‘go missing’. Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm

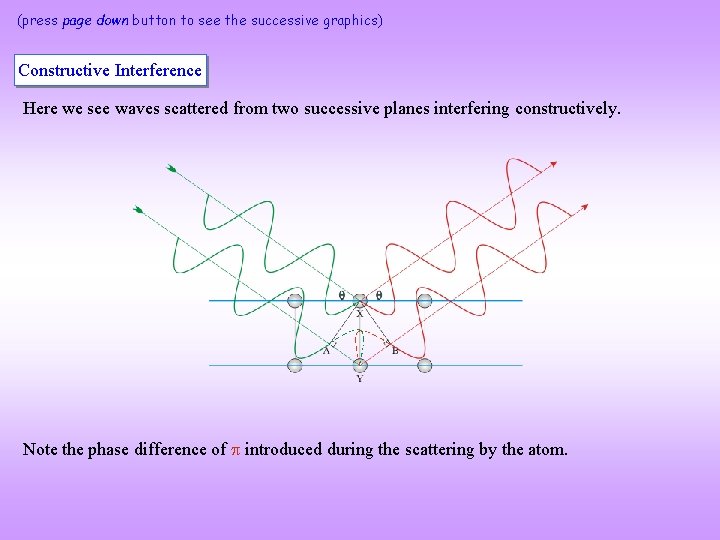
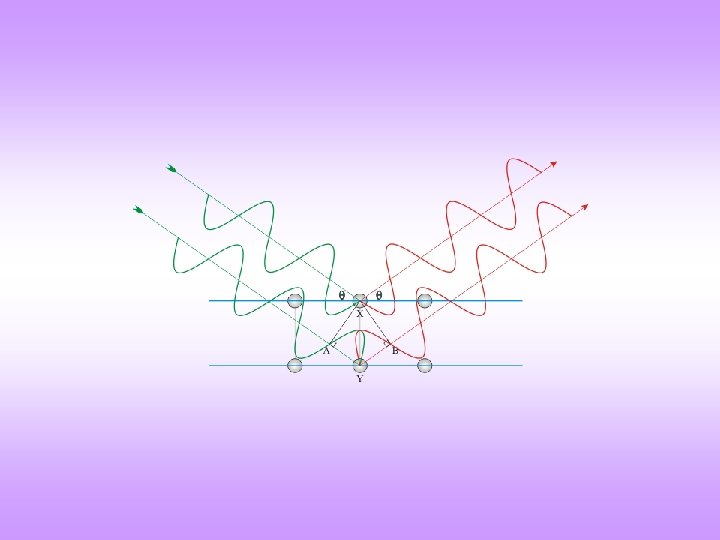
(press page down button to see the successive graphics) Constructive Interference Here we see waves scattered from two successive planes interfering constructively. Note the phase difference of introduced during the scattering by the atom.


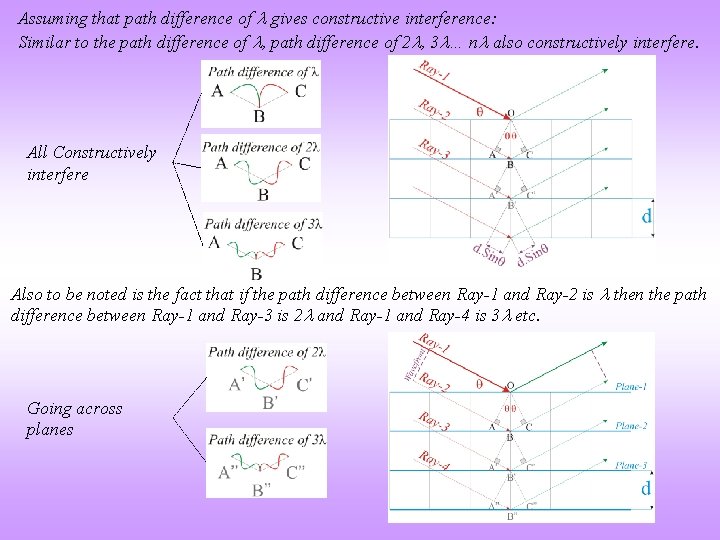
Assuming that path difference of gives constructive interference: Similar to the path difference of , path difference of 2 , 3 … n also constructively interfere. All Constructively interfere Also to be noted is the fact that if the path difference between Ray-1 and Ray-2 is then the path difference between Ray-1 and Ray-3 is 2 and Ray-1 and Ray-4 is 3 etc. Going across planes

Destructive Interference Exact destructive interference (between two planes, with path difference of /2) is easy to visualize. The angle is not Bragg’s angle (let us call it d).

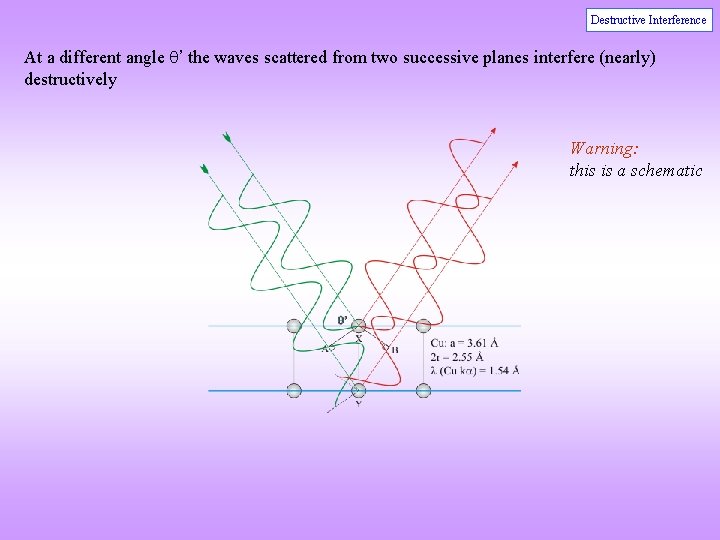
Destructive Interference At a different angle ’ the waves scattered from two successive planes interfere (nearly) destructively Warning: this is a schematic

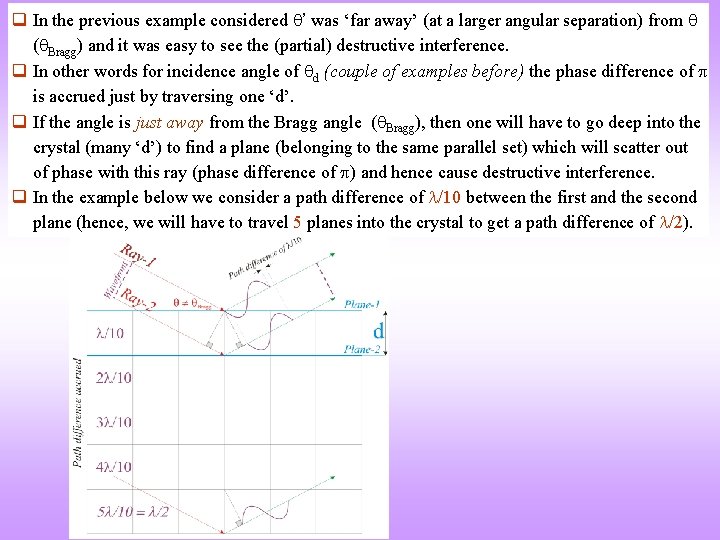
q In the previous example considered ’ was ‘far away’ (at a larger angular separation) from ( Bragg) and it was easy to see the (partial) destructive interference. q In other words for incidence angle of d (couple of examples before) the phase difference of is accrued just by traversing one ‘d’. q If the angle is just away from the Bragg angle ( Bragg), then one will have to go deep into the crystal (many ‘d’) to find a plane (belonging to the same parallel set) which will scatter out of phase with this ray (phase difference of ) and hence cause destructive interference. q In the example below we consider a path difference of /10 between the first and the second plane (hence, we will have to travel 5 planes into the crystal to get a path difference of /2).

q If such a plane (as mentioned in the page before) which scatters out of phase with a off Bragg angle ray is absent (due to finiteness of the crystal) then the ray will not be cancelled and diffraction would be observed just off Bragg angles too line broadening! (i. e. the diffraction peak is not sharp like a -peak in the intensity versus angle plot) q Line broadening can be used to calculate crystallite size (grain size). q This is one source of line broadening. Other sources include: residual strain, instrumental effects, stacking faults etc.