Understanding Basic Statistics Chapter 3 Averages and Variations

Chapter 3 Section 2 Measures of Variation

Measures of Variation ✤Range ✤Standard Deviation ✤Variance

Measures of Variation Range The difference between the largest and smallest values of a distribution.

Measures of Variation Find the range: Data: 10, 13, 17, 18 Range = largest minus smallest Range = 18 - 10 Range = 8

Measures of Variation Standard deviation a measure of the average variation of the data entries from the mean

Measures of Variation Standard deviation of a sample mean of the sample n = sample

Measures of Variation To calculate standard deviation of a sample ✴ Calculate the mean of the sample. ✴ Find the difference between each entry (x) and the mean. These differences will add up to zero. ✴ Square the deviations from the mean. ✴ Sum the squares of the deviations from the mean. ✴ Divide the sum by (n - 1) to get the variance. ✴ Take the square root of the variance to get the standard deviation.

Measures of Variation Variance The square of the standard deviation

Measures of Variation Variance of a Sample

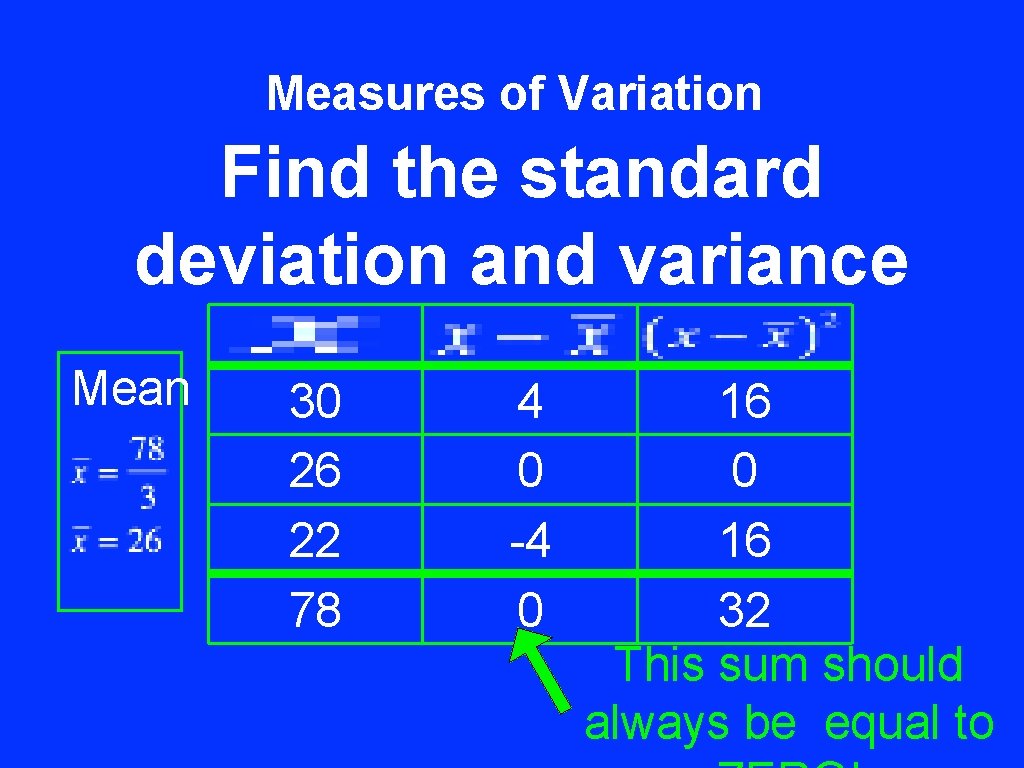
Measures of Variation Find the standard deviation and variance Mean 30 26 22 78 4 0 -4 0 16 32 This sum should always be equal to

Measures of Variation The variance

Measures of Variation The standard deviation

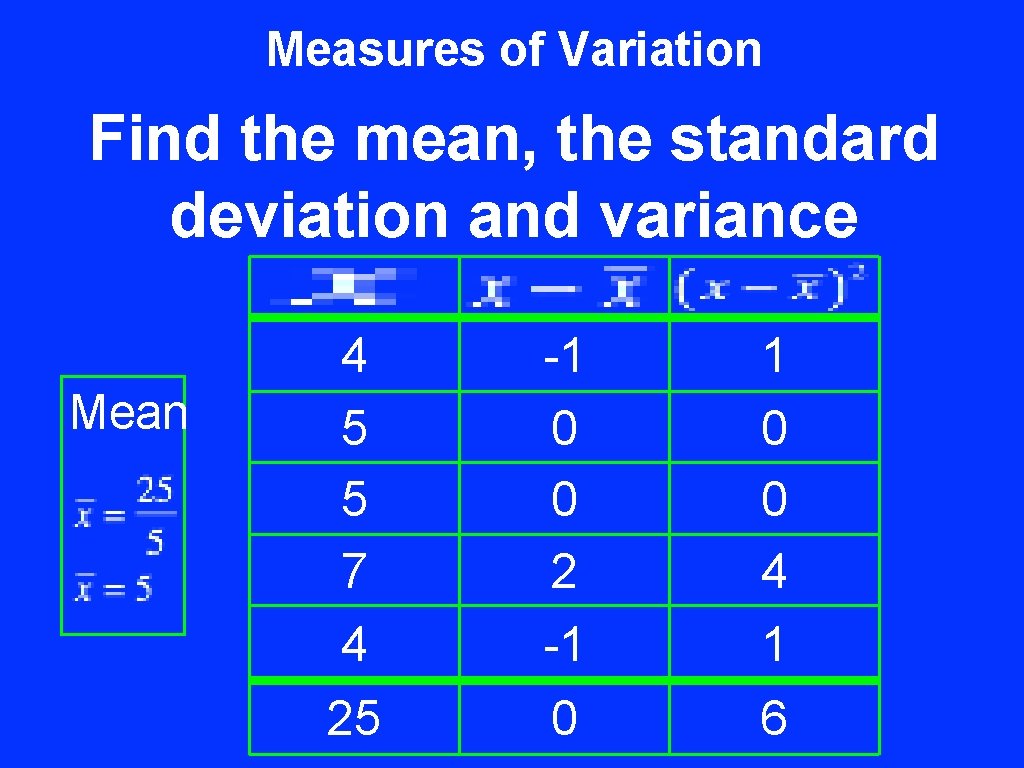
Measures of Variation Find the mean, the standard deviation and variance Mean 4 -1 1 5 5 7 0 0 2 0 0 4 4 -1 1 25 0 6

Measures of Variation The mean, the standard deviation and variance Mean Variance Standard Deviation

Measures of Variation Computation formula for sample standard deviation:

Measures of Variation To find Square the x values, then add.

Measures of Variation To find Sum the x values, then square.

Measures of Variation Use the computing formulas 2 to find s and s 4 5 5 7 4 25 16 25 25 49 16 131

Measures of Variation COEFFICIENT OF VARIATION: a measurement of the relative variability (or consistency) of data

Measures of Variation Coefficient of Variation is used to compare variability or consistency A sample of newborn infants had a mean weight of 6. 2 pounds with a standard deviation of 1 pound. A sample of three-month-old children had a mean weight of 10. 5 pounds with a standard deviation of 1. 5 pound. Which (newborns or 3 -month-olds) are more Newborns variable in weight?

Measures of Variation To compare variability, compare Coefficient of Variation The Higher the CV value the more variable the data!

Measures of Variation Use Coefficient of Variation To compare two groups of data, to answer: Which is more consistent? Which is more variable?

Measures of Variation CHEBYSHEV'S THEOREM For any set of data and for any number k, greater than one, the proportion of the data that lies within k standard deviations of the mean is at least:

Measures of Variation CHEBYSHEV'S THEOREM for k = 2 According to Chebyshev’s Theorem, at least what fraction of the data falls within “k” (k = 2) standard deviations of the mean? At LEAST 75% of the data falls within 2 standard deviations of the mean.

Measures of Variation CHEBYSHEV'S THEOREM for k = 3 According to Chebyshev’s Theorem, at least what fraction of the data falls within “k” (k = 3) standard deviations of the mean? At LEAST 88. 89% of the data falls within 3 standard deviations of the mean.

Measures of Variation CHEBYSHEV'S THEOREM for k = 4 According to Chebyshev’s Theorem, at least what fraction of the data falls within “k” (k = 4) standard deviations of the mean? At LEAST 93. 75% of the data falls within 4 standard deviations of the mean.

Measures of Variation Using Chebyshev’s Theorem A mathematics class completes an examination and it is found that the class mean is 77 and the standard deviation is 6. According to Chebyshev's Theorem, what interval would contain at least

Measures of Variation Mean = 77 Standard deviation = 6 At least 75% of the grades would be in the interval:

Measures of Variation Using Chebyshev’s Theorem A physics class completed an examination and it was determined that the class mean is 57 and the standard deviation is 13. According to Chebyshev's Theorem, what interval would contain at least

Measures of Variation Mean = 57 Standard deviation = 13 At least 88. 89% of the grades would be in the interval:

The End