Understanding and Comparing Distributions Another Useful Graphical Method

Understanding and Comparing Distributions Another Useful Graphical Method: Boxplots

Pulse Rates n = 138 Median: mean of pulses in locations 69 & 70: median= (70+70)/2=70 Q 1: median of lower half (lower half = 69 smallest pulses); Q 1 = pulse in ordered position 35; Q 1 = 63 Q 3 median of upper half (upper half = 69 largest pulses); Q 3= pulse in position 35 from the high end; Q 3=78

Recall the 5 -number summary of data Minimum Q 1 median Q 3 maximum n Pulse data 5 -number summary 45 63 70 78 111 A boxplot is a graphical display of the 5 number summary n §

Example n Consider the data shown at the left. – The data values 6. 1, 5. 6, …, are in the right column – They are arranged in decreasing order from 6. 1 (data rank of 25 shown in far left column) to 0. 6 (data rank of 1 in far left column) – The center column shows the ranks of the quartiles (in blue) from each end of the data and from the overall median (in yellow)

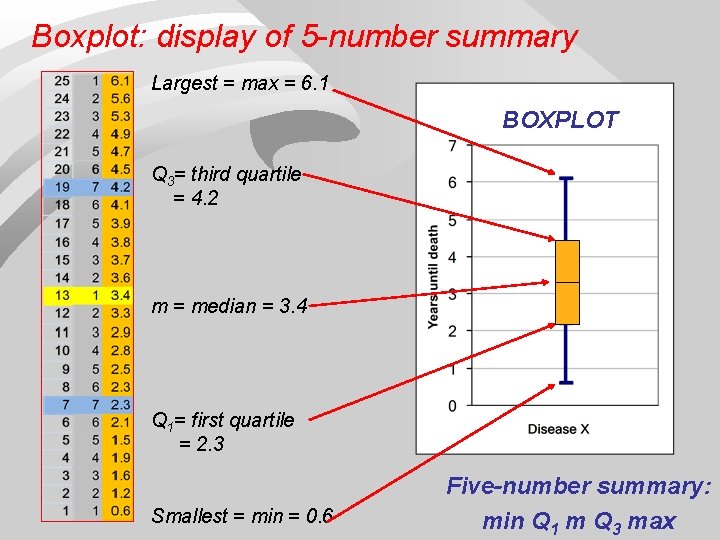
Boxplot: display of 5 -number summary Largest = max = 6. 1 BOXPLOT Q 3= third quartile = 4. 2 m = median = 3. 4 Q 1= first quartile = 2. 3 Smallest = min = 0. 6 Five-number summary: min Q 1 m Q 3 max

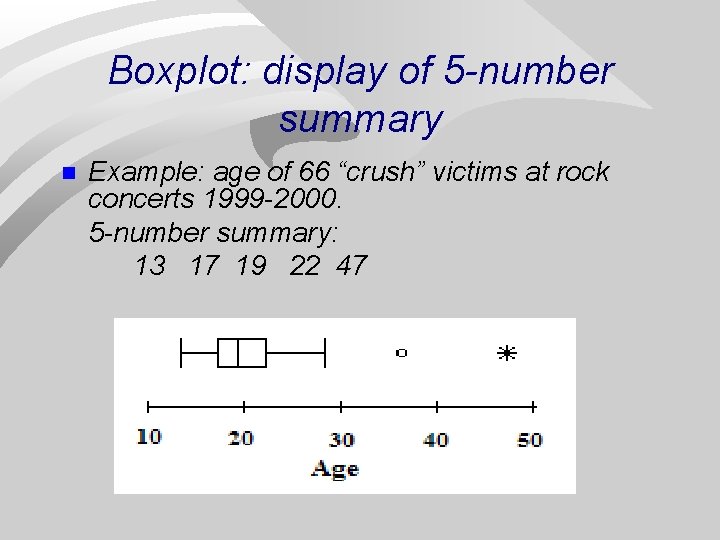
Boxplot: display of 5 -number summary n Example: age of 66 “crush” victims at rock concerts 1999 -2000. 5 -number summary: 13 17 19 22 47

Boxplot construction 1) construct box with ends located at Q 1 and Q 3; in the box mark the location of median (usually with a line or a “+”) 2) fences are determined by moving a distance 1. 5(IQR) from each end of the box; 2 a) upper fence is 1. 5*IQR above the upper quartile 2 b) lower fence is 1. 5*IQR below the lower quartile Note: the fences only help with constructing the boxplot; they do not appear in the final boxplot display

Box plot construction (cont. ) 3) whiskers: draw lines from the ends of the box left and right to the most extreme data values found within the fences; 4) outliers: special symbols represent each data value beyond the fences; 4 a) sometimes a different symbol is used for “far outliers” that are more than 3 IQRs from the quartiles

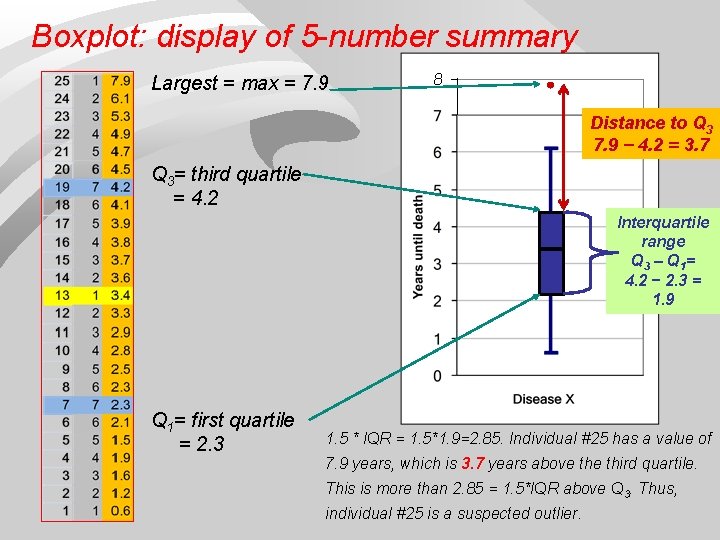
Boxplot: display of 5 -number summary Largest = max = 7. 9 8 BOXPLOT Distance to Q 3 7. 9 − 4. 2 = 3. 7 Q 3= third quartile = 4. 2 Interquartile range Q 3 – Q 1= 4. 2 − 2. 3 = 1. 9 Q 1= first quartile = 2. 3 1. 5 * IQR = 1. 5*1. 9=2. 85. Individual #25 has a value of 7. 9 years, which is 3. 7 years above third quartile. This is more than 2. 85 = 1. 5*IQR above Q 3. Thus, individual #25 is a suspected outlier.

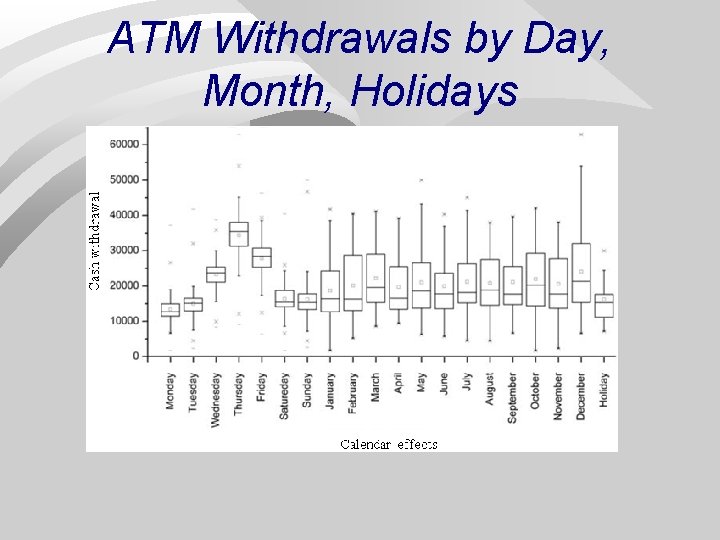
ATM Withdrawals by Day, Month, Holidays

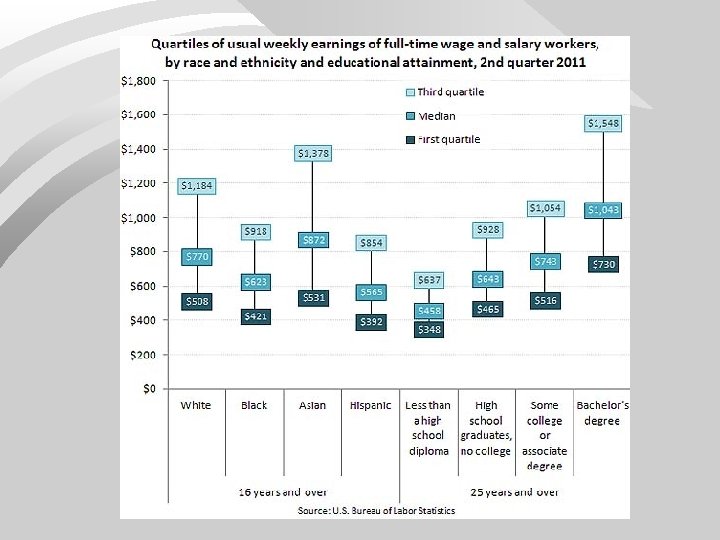
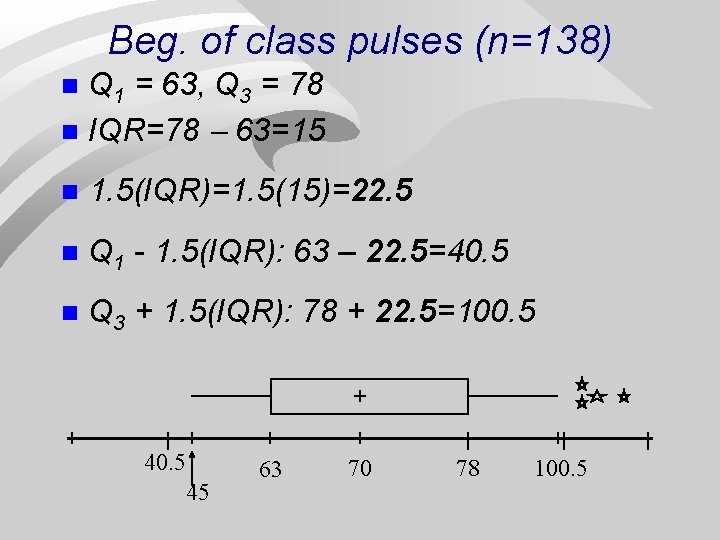
Beg. of class pulses (n=138) Q 1 = 63, Q 3 = 78 n IQR=78 63=15 n n 1. 5(IQR)=1. 5(15)=22. 5 n Q 1 - 1. 5(IQR): 63 – 22. 5=40. 5 n Q 3 + 1. 5(IQR): 78 + 22. 5=100. 5 45 63 70 78 100. 5

Below is a box plot of the yards gained in a recent season by the 136 NFL receivers who gained at least 50 yards. What is the approximate value of Q 3 ? 0 136 273 410 547 684 821 958 1095 1232 1369 Pass Catching Yards by Receivers 1. 2. 3. 4. 45 0 750 215 545 10 Countdown

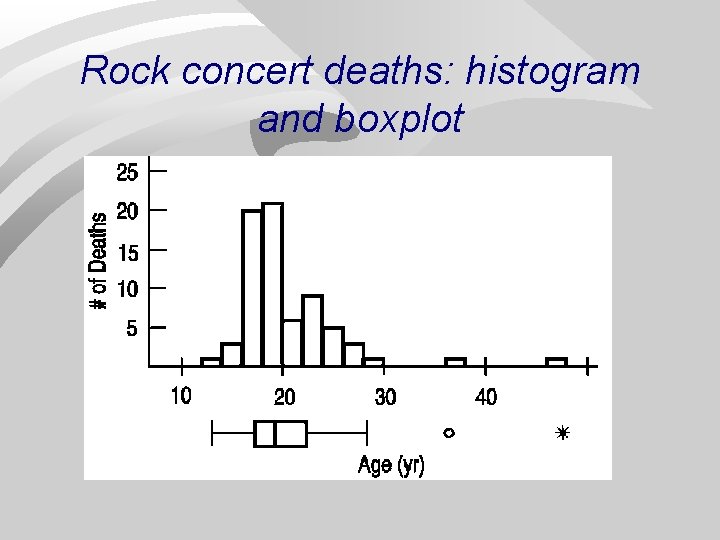
Rock concert deaths: histogram and boxplot

Automating Boxplot Construction Excel “out of the box” does not draw boxplots. n Many add-ins are available on the internet that give Excel the capability to draw box plots. n Statcrunch (http: //statcrunch. stat. ncsu. edu) draws box plots. n

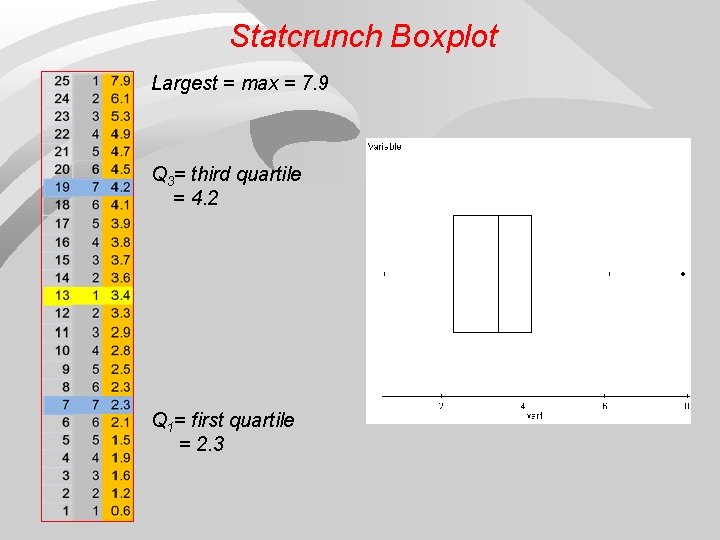
Statcrunch Boxplot Largest = max = 7. 9 Q 3= third quartile = 4. 2 Q 1= first quartile = 2. 3

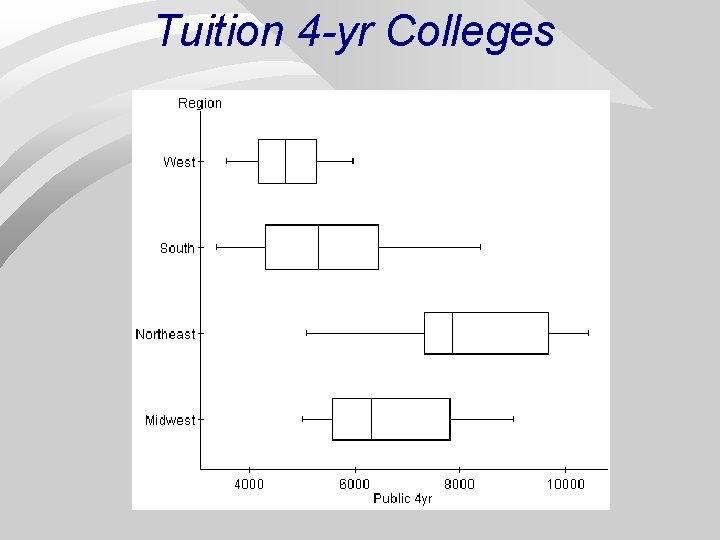
Tuition 4 -yr Colleges

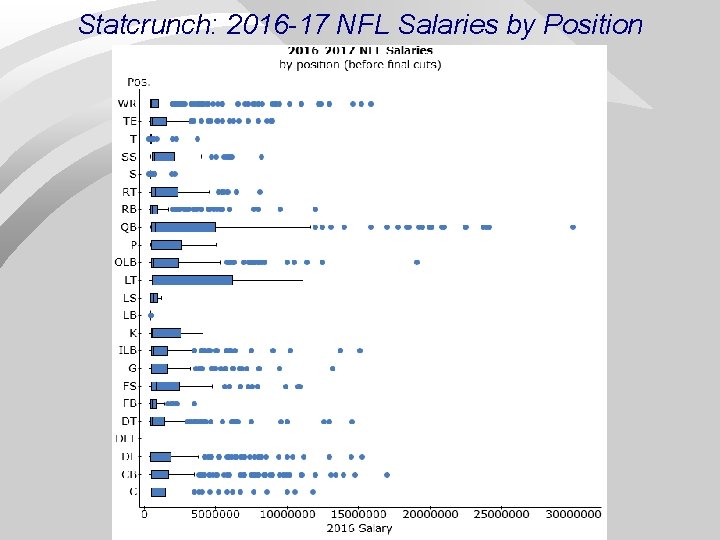
Statcrunch: 2016 -17 NFL Salaries by Position

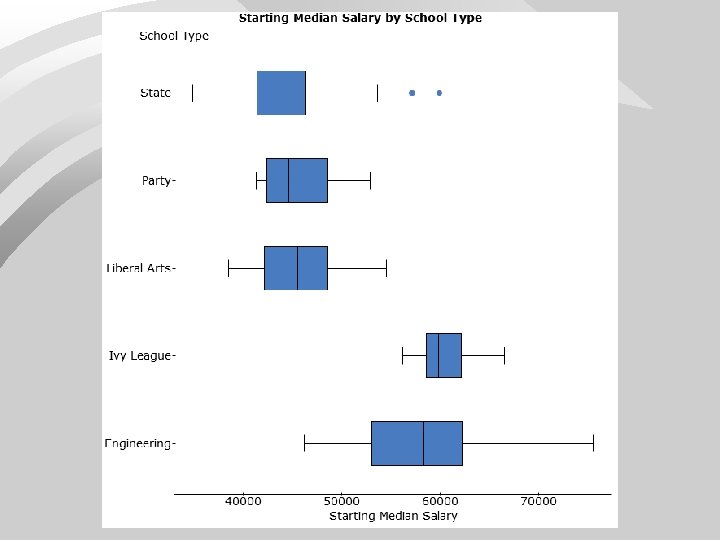
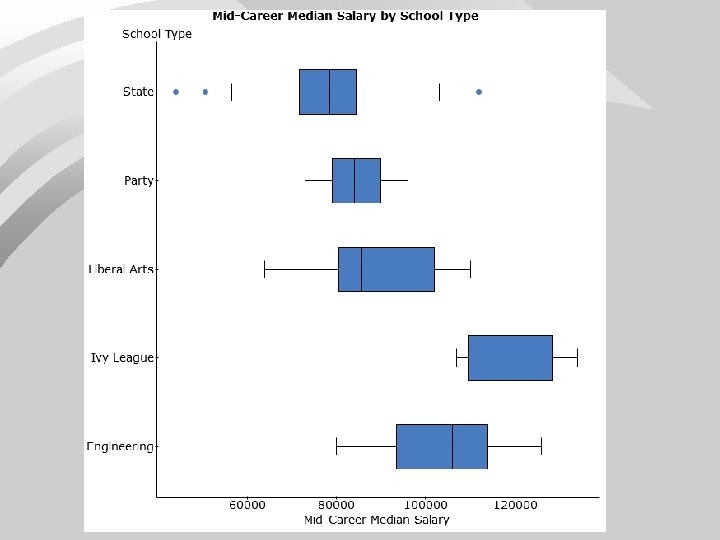
TA-DAAA! The End