Unconstrained Optimization Rong Jin Logistic Regression The optimization

Unconstrained Optimization Rong Jin

Logistic Regression The optimization problem is to find weights w and b that maximizes the above log-likelihood How to do it efficiently ?

Gradient Ascent o Compute the gradient o Increase weights w and threshold b in the gradient direction

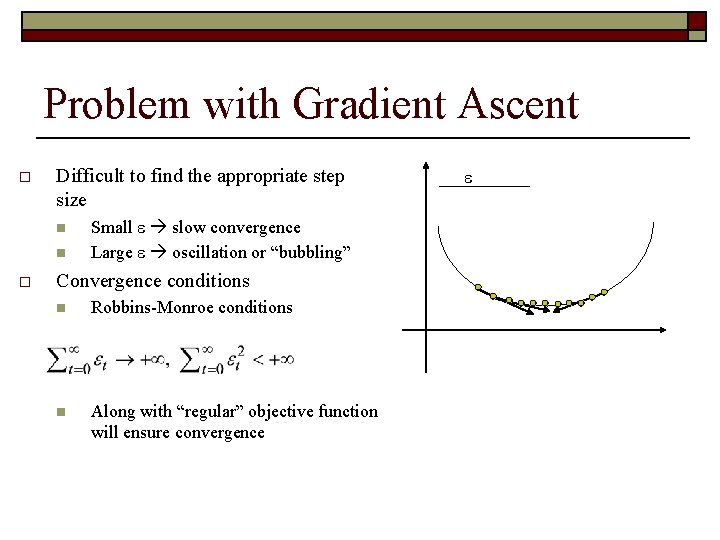
Problem with Gradient Ascent o Difficult to find the appropriate step size n n o Small slow convergence Large oscillation or “bubbling” Convergence conditions n Robbins-Monroe conditions n Along with “regular” objective function will ensure convergence

Newton Method o o Utilizing the second order derivative Expand the objective function to the second order around x 0 o The minimum point is Newton method for optimization o Guarantee to converge when the objective function is convex o

Multivariate Newton Method o Object function comprises of multiple variables n Example: logistic regression model Text categorization: thousands of words thousands of variables Multivariate Newton Method n o n Multivariate function: n First order derivative a vector n Second order derivative Hessian matrix o o Hessian matrix is mxm matrix Each element in Hessian matrix is defined as:

Multivariate Newton Method o Updating equation: o Hessian matrix for logistic regression model o Can be expensive to compute n n n Example: text categorization with 10, 000 words Hessian matrix is of size 10, 000 x 10, 000 100 million entries Even worse, we have compute the inverse of Hessian matrix H-1

Quasi-Newton Method o Approximate the Hessian matrix H-1 with another B matrix: o B is update iteratively (BFGS): n Utilizing derivatives of previous iterations

Limited-Memory Quasi-Newton o Quasi-Newton n n o Avoid computing the inverse of Hessian matrix But, it still requires computing the B matrix large storage Limited-Memory Quasi-Newton (L-BFGS) n Even avoid explicitly computing B matrix n B can be expressed as a product of vectors Only keep the most recently vectors of n (3~20)

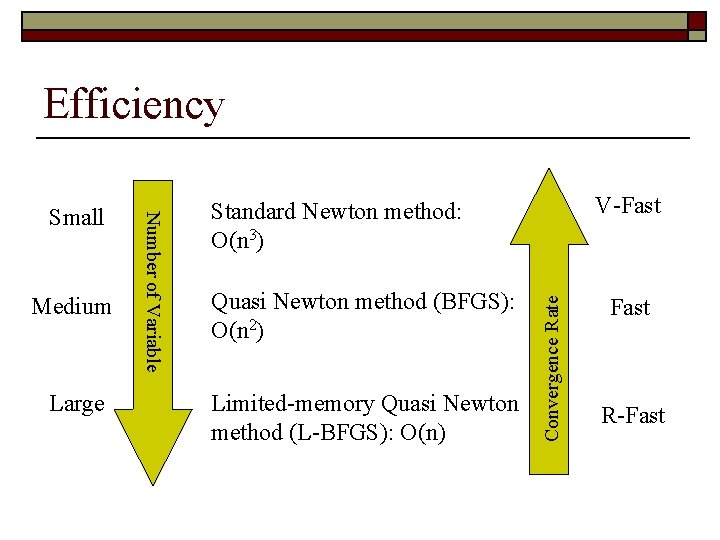
Efficiency Large V-Fast Standard Newton method: O(n 3) Quasi Newton method (BFGS): O(n 2) Limited-memory Quasi Newton method (L-BFGS): O(n) Convergence Rate Medium Number of Variable Small Fast R-Fast

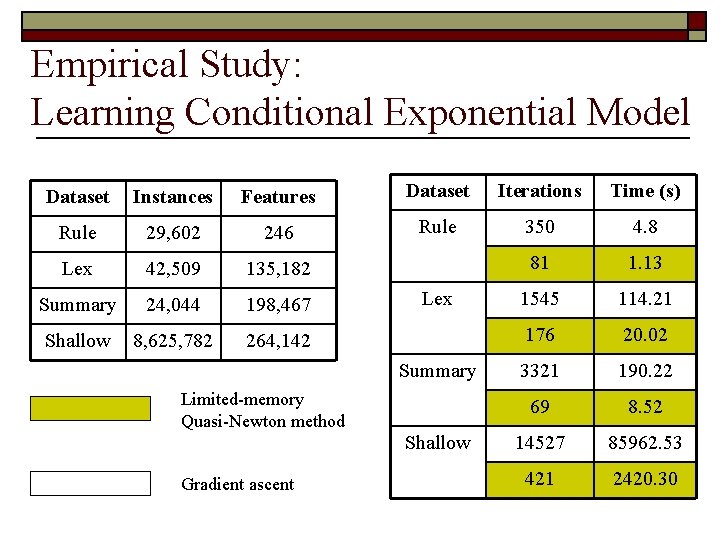
Empirical Study: Learning Conditional Exponential Model Dataset Instances Features Dataset Iterations Time (s) Rule 29, 602 246 Rule 350 4. 8 Lex 42, 509 135, 182 81 1. 13 Summary 24, 044 198, 467 1545 114. 21 Shallow 8, 625, 782 264, 142 176 20. 02 3321 190. 22 69 8. 52 14527 85962. 53 421 2420. 30 Lex Summary Limited-memory Quasi-Newton method Shallow Gradient ascent

Free Software o http: //www. ece. northwestern. edu/~nocedal/so ftware. html n n L-BFGSB

Linear Conjugate Gradient Method o Consider optimizing the quadratic function o Conjugate vectors n The set of vector {p 1, p 2, …, pl} is said to be conjugate with respect to a matrix A if n Important property o n The quadratic function can be optimized by simply optimizing the function along individual direction in the conjugate set. Optimal solution: o k is the minimizer along the kth conjugate direction

Example o Minimize the following function o Matrix A o Conjugate direction o Optimization n First direction, x 1 = x 2=x: Second direction, x 1 =- x 2=x: Solution: x 1 = x 2=1

How to Efficiently Find a Set of Conjugate Directions o Iterative procedure n Given conjugate directions {p 1, p 2, …, pk-1} n Set pk as follows: n Theorem: The direction generated in the above step is conjugate to all previous directions {p 1, p 2, …, pk-1}, i. e. , n Note: compute the k direction pk only requires the previous direction pk-1

Nonlinear Conjugate Gradient o o Even though conjugate gradient is derived for a quadratic objective function, it can be applied directly to other nonlinear functions Several variants: n n Fletcher-Reeves conjugate gradient (FR-CG) Polak-Ribiere conjugate gradient (PR-CG) o o More robust than FR-CG Compared to Newton method n n No need for computing the Hessian matrix No need for storing the Hessian matrix