Uncertainty is Pervasive u What is uncertain in

Uncertainty is Pervasive u What is uncertain in economic systems? – future prices – future availability of commodities – present and future actions of other people

Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.

States of Nature (SON) u Possible SONs: – car accident (a) – no car accident (na) occurs with probability a, does not with probability na : u Accident a + na = 1. u Accident causes a loss of $L.

Contingencies u. A contract implemented only when a particular SON occurs is statecontingent. u E. g. : the insurer pays only if there is an accident.

Contingencies u. A state-contingent consumption plan is implemented only when a particular SON occurs. [Example] take a vacation only if there is no accident.

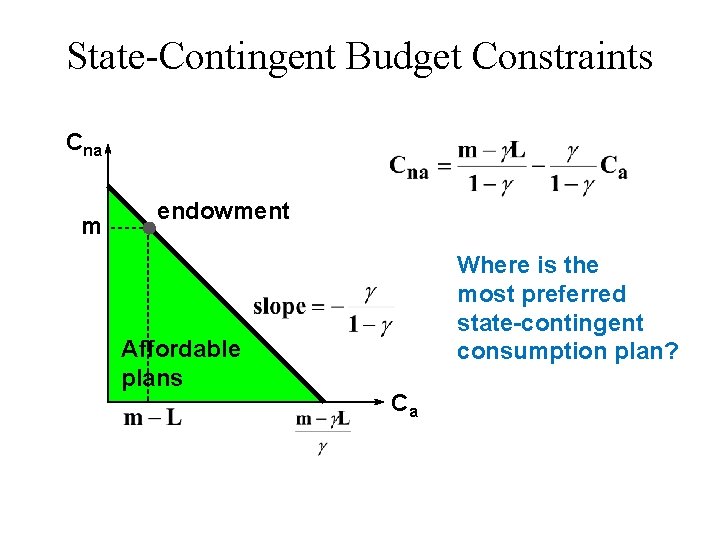
State-Contingent Budget Constraints $1 of accident insurance costs u Consumer has $m of wealth u Cna is consumption value in the noaccident state. u Ca is consumption value in the accident state. u Each

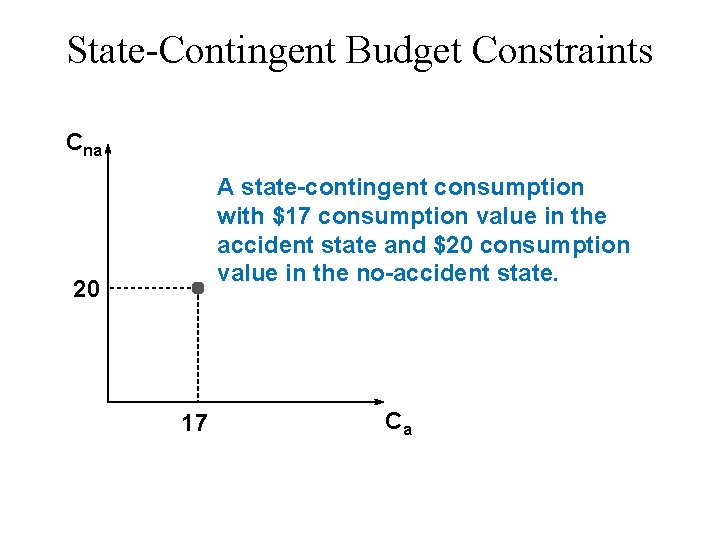
State-Contingent Budget Constraints Cna A state-contingent consumption with $17 consumption value in the accident state and $20 consumption value in the no-accident state. 20 17 Ca

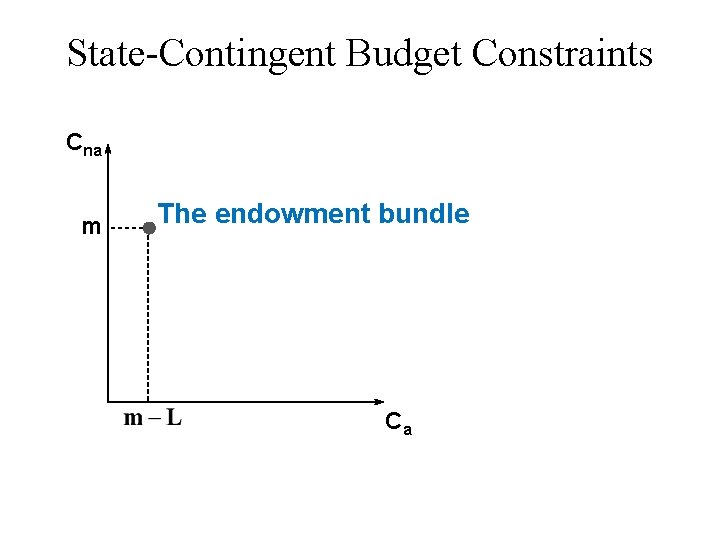
State-Contingent Budget Constraints u Without insurance: Ca = m – L Cna = m

State-Contingent Budget Constraints Cna m The endowment bundle Ca

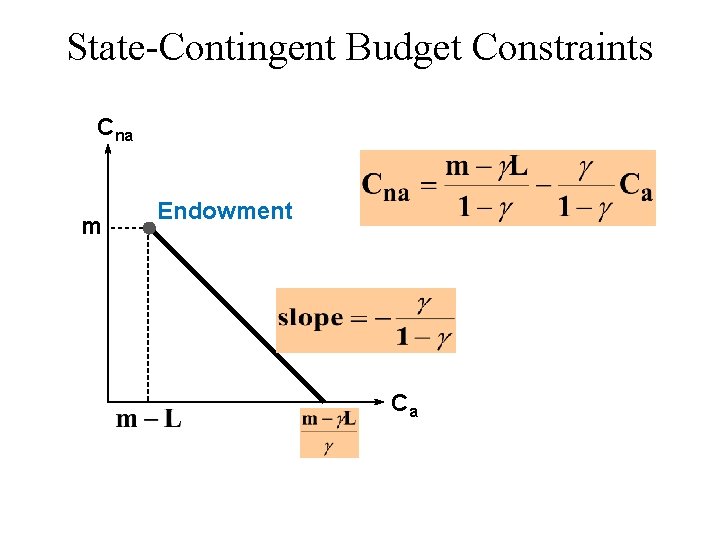
State-Contingent Budget Constraints u Buy $K of accident insurance Cna = m - K Ca = m - L - K + K = m - L + (1 - )K

State-Contingent Budget Constraints u Buy $K of accident insurance u Cna = m - K u Ca = m - L - K + K = m - L + (1 - )K u So K = (Ca - m + L)/(1 - ) u And: Cna = m - (Ca - m + L)/(1 - )

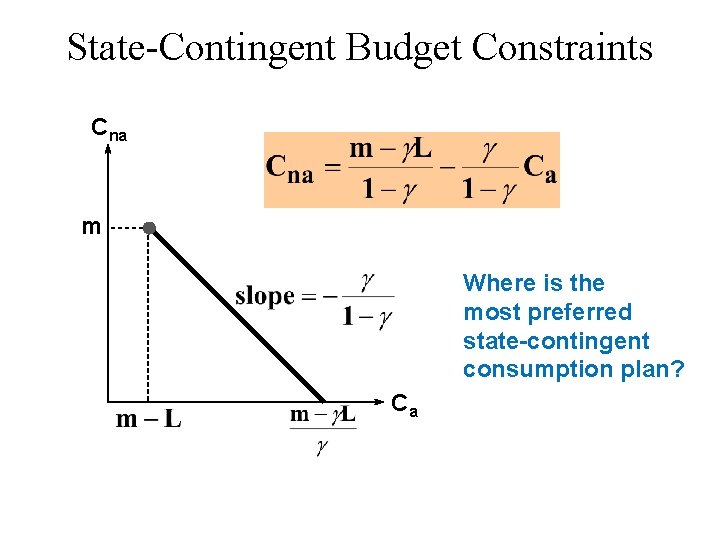
State-Contingent Budget Constraints u Buy $K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - ) u And Cna = m - (Ca - m + L)/(1 - ) u I. e. :

State-Contingent Budget Constraints Cna m Endowment Ca

State-Contingent Budget Constraints Cna m Where is the most preferred state-contingent consumption plan? Ca

Preferences Under Uncertainty u Think of a lottery. u Win $90 with p=1/2, and win $0 with p=1/2. u U($90)=12 U($0) = 2

Preferences Under Uncertainty u Expected utility is:

Preferences Under Uncertainty u Expected is: money value of the lottery

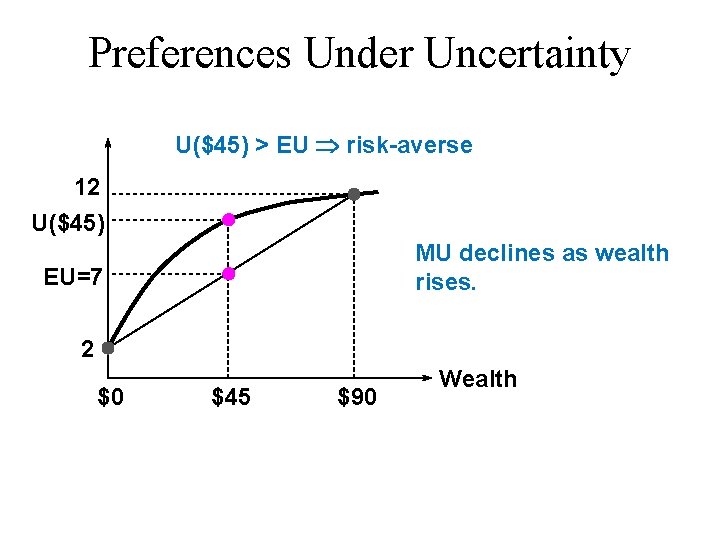
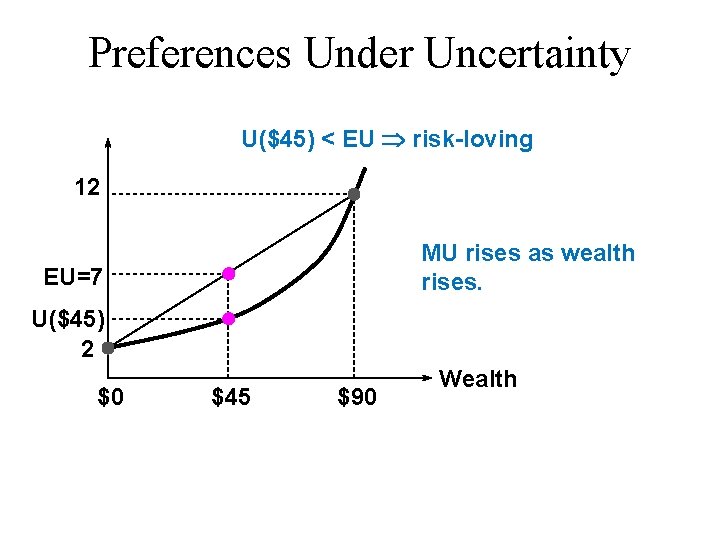
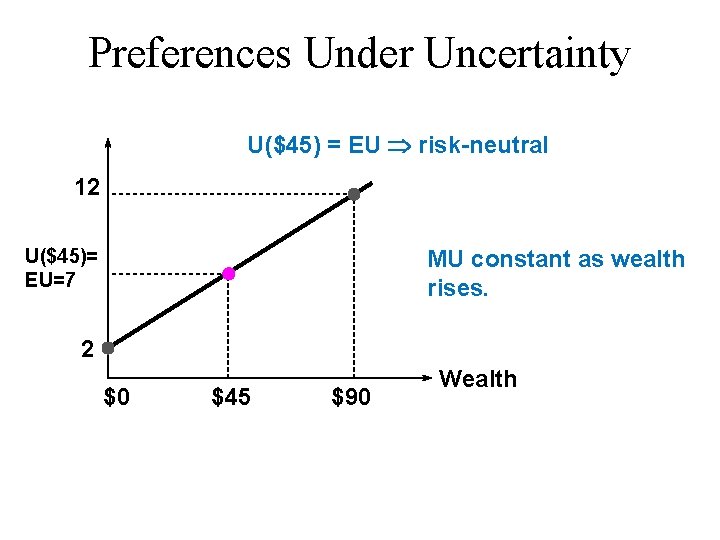
Preferences Under Uncertainty u EU = 7 and EM = $45 u U($45) > 7 $45 for sure is preferred to the lottery risk-averse u U($45) < 7 the lottery is preferred to $45 for sure risk-loving u U($45) = 7 the lottery is preferred equally to $45 for sure risk-neutral

Preferences Under Uncertainty U($45) > EU risk-averse 12 U($45) MU declines as wealth rises. EU=7 2 $0 $45 $90 Wealth

Preferences Under Uncertainty U($45) < EU risk-loving 12 MU rises as wealth rises. EU=7 U($45) 2 $0 $45 $90 Wealth

Preferences Under Uncertainty U($45) = EU risk-neutral 12 U($45)= EU=7 MU constant as wealth rises. 2 $0 $45 $90 Wealth

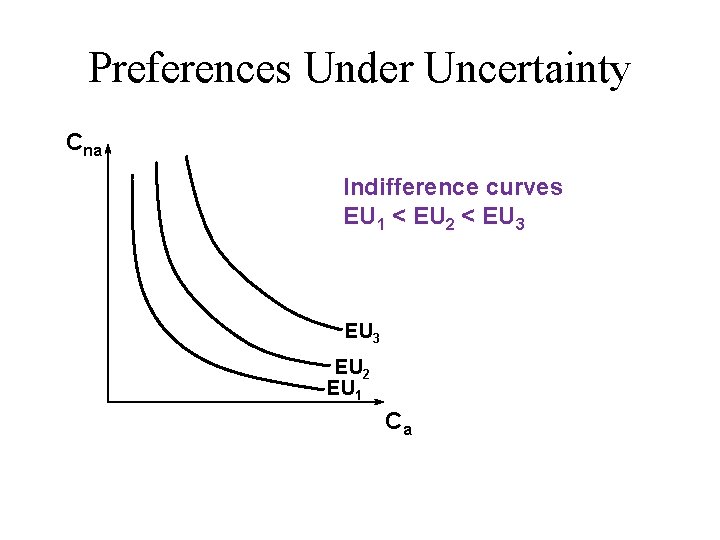
Preferences Under Uncertainty u State-contingent consumption plans that give equal expected utility are equally preferred.

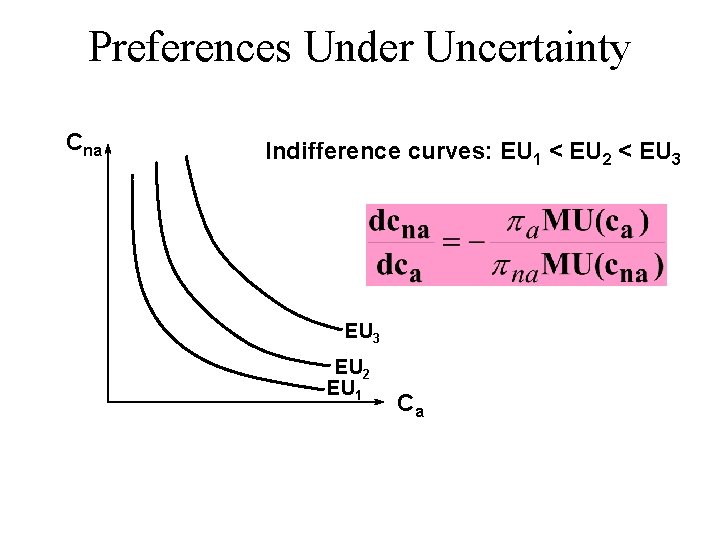
Preferences Under Uncertainty Cna Indifference curves EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca

Preferences Under Uncertainty u What is the MRS of an indifference curve? u Get consumption c 1 with prob. 1 and c 2 with prob. 2 ( 1 + 2 = 1) u EU = 1 U(c 1) + 2 U(c 2) u For constant EU: d. EU = 0

Preferences Under Uncertainty

Preferences Under Uncertainty Cna Indifference curves: EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca

Choice Under Uncertainty [Q] How is a rational choice made under uncertainty? [A] Choose the most preferred affordable state-contingent consumption plan.

State-Contingent Budget Constraints Cna m endowment Affordable plans Where is the most preferred state-contingent consumption plan? Ca

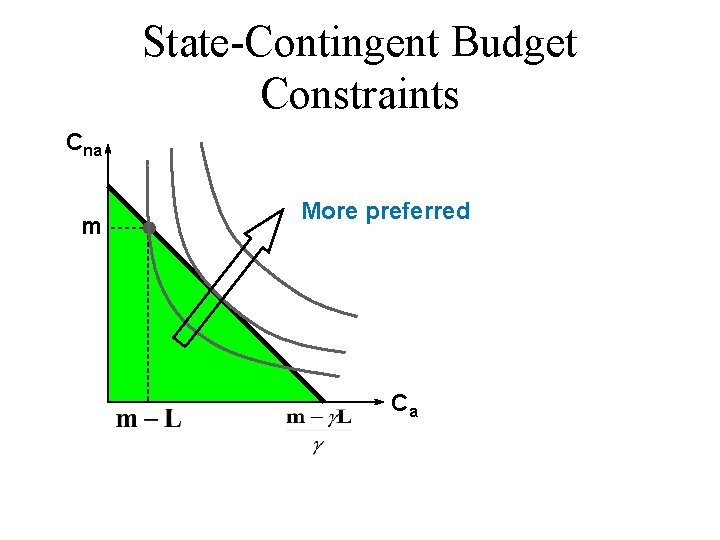
State-Contingent Budget Constraints Cna m More preferred Ca

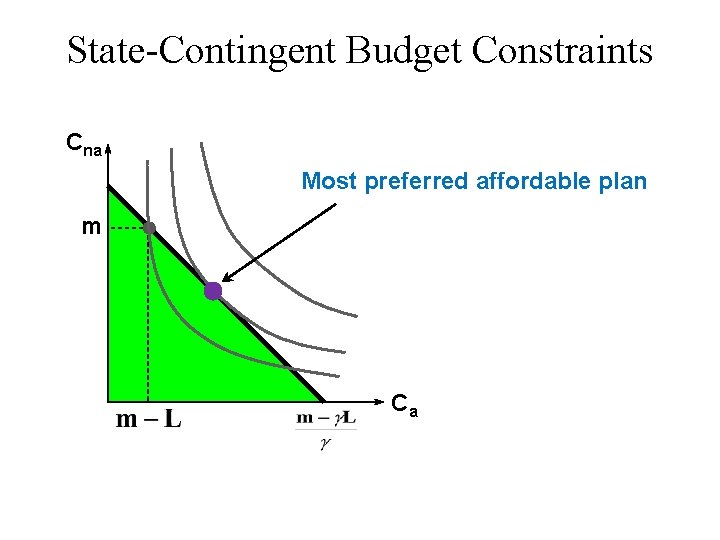
State-Contingent Budget Constraints Cna Most preferred affordable plan m Ca

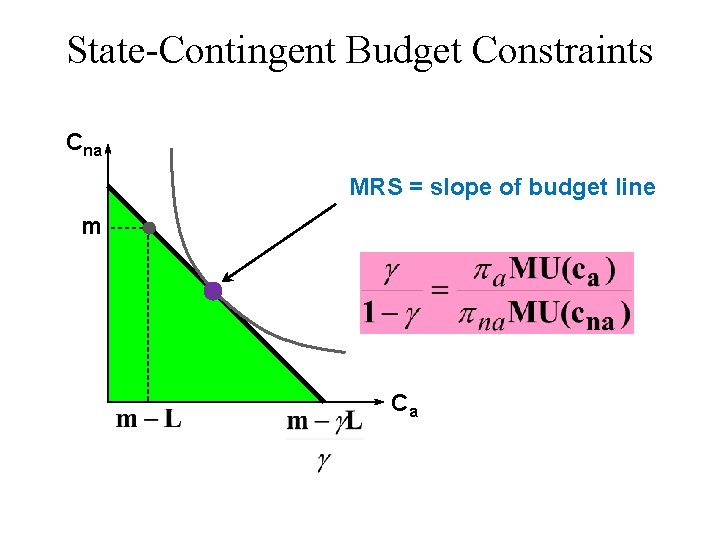
State-Contingent Budget Constraints Cna MRS = slope of budget line m Ca

Competitive Insurance u Suppose entry to the insurance industry is free. u Expected economic profit = 0: K - a. K - (1 - a)0 = ( - a)K = 0 u I. e. : free entry = a u Insurance is actuarially fair, if: price of $1 insurance = accident probability.

Competitive Insurance u When insurance is fair, rational insurance choices satisfy: u I. e. : u Marginal utility of income must be the equal in both states.

Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion MU(c) as c u Hence: u I. e. full-insurance

Unfair Insurance u Suppose insurers make positive expected economic profit. u I. e. K - a. K - (1 - a)0 = ( - a)K > 0 u Then > a

Unfair Insurance u Rational choice requires u Since u Hence for a risk-averter. u I. e. a risk-averter buys less than full unfair insurance.

Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods [Franco ? Modigliani (Nobel 1985, 1918 -2003)]

Diversification u Two firms, A and B. Shares cost $10. u With p=½: A’s profit is $100; B’s profit is $20 u With p=½: A’s profit is $20; B’s profit is $100 u You have $100. How to invest?

Diversification u Buy only firm A’s stock? u $100/10 = 10 shares. u You earn $1000 with p=1/2, and $200 with p=1/2. u Expected earning: $500 + $100 = $600

Diversification u Buy only firm B’s stock? u $100/10 = 10 shares. u You earn $1000 with p=1/2, and $200 with p=1/2. u Expected earning: $500 + $100 = $600

Diversification u Buy 5 shares in each firm? u You earn $600 for sure. u Diversification has maintained expected earning and lowered risk.

Diversification u Typically, diversification lowers expected earnings in exchange for lowered risk.

Risk Spreading/Mutual Insurance u 100 risk-neutral persons each independently risk a $10 K loss. u Loss probability = 1% u Initial wealth is $40 K u No insurance: expected wealth is

Risk Spreading/Mutual Insurance u Mutual insurance: Expected loss is u Each of the 100 persons pays $1 into a mutual insurance fund u Mutual insurance: expected wealth is u Risk-spreading benefits all ex ante!