Uncertainty in AI Rule strengths or priorities in

Uncertainty in AI

• Rule strengths or priorities in Expert Systems • . . . an old ad-hoc approach (with unclear semantics) • penguin(x) → 0. 9 flies(x) • bird(x) → 0. 5 flies(x) • example: • can assign 'salience' (integers) to defrules in Jess • this will determine the order in which rules fire in the forward-chaining

Probability • encode knowledge in the form of prior probabilities and conditional probabilities • • P(x speaks portugese|x is from Brazil)=0. 9 P(x speaks portugese)=0. 012 P(x is from Brazil)=0. 007 P(x flies|x is a bird)=0. 8 (? ) • inference is done by calculating posterior probabilities given evidence • compute P(cavity | toothache, flossing, dental history, recent consumption of candy. . . ) • compute P(fed will raise interest rate | employment=5%, inflation=0. 5%, GDP=2%, recent

• Many modern knowledge-based systems are based on probabilistic inference • including Bayesian networks, Hidden Markov Models, Markov Decision Problems • example: Bayesian networks are used for inferring user goals or help needs from actions like mouse clicks in an automated software help system (think 'Clippy') • Decision Theory combines utilities with probabilities of outcomes to decide actions to tak • the challenge is capturing all the numbers needed for the prior and conditional probabilities • objectivists (frequentists) - probabilities represent outcomes of trials/experiments • subjectivists - probabilities are degrees of belief • probability and statistics is at the core of many Machine Learning algorithms

Causal vs. diagnostic knowledge • causal: P(x has a toothache|x has a cavity)=0. 9 • diagnostic: P(x has a cavity|x has a toothache)=0. 5 • typically it is easier to articulate knowledge in the causal direction, but we often want to use it in a diagnostic way to make inferences from observations

Bayes' Rule • product rule : P(A, B) joint = P(A|B)*P(B) • Bayes' Rule: convert between causal and diagnostic H = hypothesis (cause, disease) E = evidence (effect, symptoms)

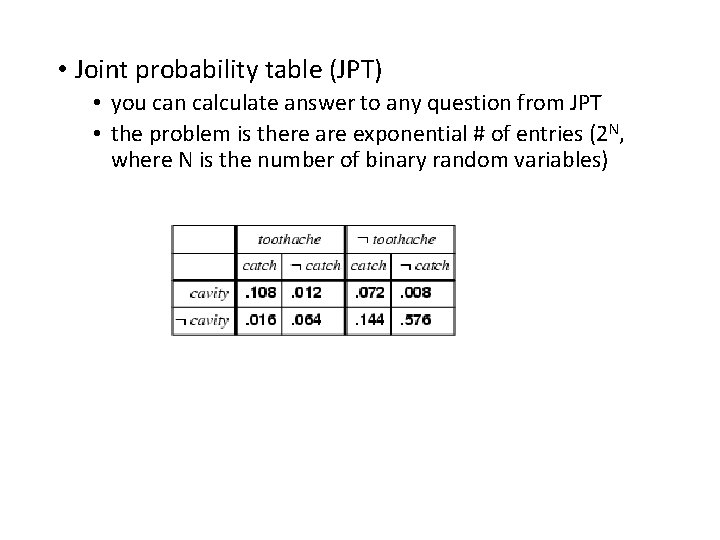
• Joint probability table (JPT) • you can calculate answer to any question from JPT • the problem is there are exponential # of entries (2 N, where N is the number of binary random variables)

• Joint probability table (JPT) • you can calculate answer to any question from JPT • the problem is there are exponential # of entries (2 N, where N is the number of binary random variables) P( cavity | toothache)

• Joint probability table (JPT) • you can calculate answer to any question from JPT • the problem is there are exponential # of entries (2 N, where N is the number of binary random variables) P( cavity | toothache) = P( cavity toothache) / P(toothache) = 0. 016+0. 064 / (0. 108 + 0. 012 + 0. 016 + 0. 064) = 0. 4

• Joint probability table (JPT) • you can calculate answer to any question from JPT • the problem is there are exponential # of entries (2 N, where N is the number of binary random variables) P( cavity | toothache) = P( cavity toothache) / P(toothache) = 0. 016+0. 064 / (0. 108 + 0. 012 + 0. 016 + 0. 064) = 0. 4

Solution to reduce complexity: Employ the Independence Assumption Most variables are not strictly independent, in that there is a statistical association (but which is cause? effect? ). However, some many variables are conditionally independent. P(A, B|C) = P(A|C)P(B|C)

Bayesian networks note: absence of link between Burglary and John. Calls means John. Calls is conditionally independent of Burglary given Alarm

Equation for full joint probability

• If some variables are unknown, you have to marginalize (sum) over them. • There are many algorithms for trying to do efficient computation with Bayesian networks. • For example: • variable elimination • factor graphs and message passing • sampling

Lumiere (Microsoft) – Office Assistant

Hidden Markov Models • transition probabilities and emission probabilities • Viterbi algorithm for computing most probable state sequence from observations