Uncertainty and Semantic web Jennifer Sleeman Agenda Define

Uncertainty and Semantic web Jennifer Sleeman

Agenda Ø Define uncertainty Ø Provide background Ø Show areas of research Ø Highlight various approaches Ø Provide a demonstration of Pronto

Definition - Uncertainty Ø Knowledge can be inaccurate or incomplete Ø Knowledge can be imprecise or “fuzzy” …. leads to uncertainty…

Definition - Uncertainty Machine-readable information Ø Applications that work with random information (image processing, geospatial, information retrieval, etc. ) Ø Ontology concept definitions Ø l l Ø Vague concepts: Tall, Small, Big, …. Green, Blue, …. Few, Many, …. Semantic web services …. work with uncertainty…

Background – Description Logic Naming Conventions Taken from Wikipedia [12].

Is representing uncertainty necessary? Ø Tim Berner-Lee rejection of uncertainty l l Not necessary [7] Scalability issues [7]

Can you describe knowledge using a “monotonic bivalent language”[7]?

What about grey? Uncertainty

Is it necessary? Taken from [5] presented at the URSW 2008.

General Approaches to Uncertainty and Semantic Web l Incomplete/Distorted knowledge [1] • Possibility degrees alternatives l Inability to define concepts precisely [1] • Degree of truth l Conflicting alternatives [1] • Degree of probability According to [1], since how we solve uncertainty problems depends upon the domain, it is hard to define a single language extension.

Areas of Research (based upon 2007/2008 URSW Conference agendas) Ø Extending Semantic Web to support uncertainty Ø Fuzzy theory Ø Probability theory Ø Uncertainty and Ontologies Ø Uncertainty and Web Services

Extending the Semantic Web Ø Extend Semantic Web languages to support probabilistic, possibilistic, and fuzzy reasoning Ø Can be at the ontology layer or the rules layer Ø Within the ontology layer proposals for: l l Syntax and Semantics Logical Formalisms

Fuzzy Theory “…In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition — an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval [0, 1]…”[10]

Fuzzy Approaches Ø Extending languages such as OWL with fuzzy extensions Ø Extending Description Logic with fuzzy extensions Ø If a language is extended, one must provide a way to support reasoning of the language with the fuzzy extension

Rules and Uncertainty Rules Interchange Format Ø Rules Markup Language Ø l For representing/interchanging rules Attempt to provide ways to represent various types of uncertainty [1] Ø Not as much recent attention as ontology layer Ø fuzzy Rule. ML defines way to specify membership degree [1] Ø l Example: Taken from [1].

Fuzzy RDF Extends syntax and semantics of RDF Ø Triple extended to support real number on the interval [0, 1] Ø l Ø n: s p o [13] Interpretation l l Subject, object has degree of membership to extension of predicate [13] Satisfies statement if • Membership degree of {subject, object} to the extension of the predicate is >= to n [13]

Fuzzy RDF Ø RDFS extended l l “Class extensions are fuzzy sets of domain elements” [13] Domains are fuzzy and their assignment to properties can also be fuzzy [13] Ø Inference engines can be extended to support such fuzziness

Fuzzy Description Logic Ø Fuzzy l One such proposal Ø Solve problem of representing and reasoning of fuzzy concepts Ø With concrete domains – reasoning using concrete data types Ø With fuzzy version domains are fuzzy Ø Modifiers are supported (very, slightly, etc. ) [12]

Fuzzy Description Logic Non-fuzzy Concrete Domain: Concrete Fuzzy Domain: Taken from [12].

Fuzzy Description Logic Ø Interpretations are fuzzy l From satisfied/unsatisfied to a degree of truth [0, 1] Satisfiability of fuzzy axiom given fuzzy interpretation [12] Ø “Fuzzy axiom a logical consequence of a knowledge base iff every model in the knowledge base satisfies the fuzzy axiom” [12] Ø Reasoning a problem Ø l Computationally no calculus exists to check for satisfiability of a fuzzy knowledge model [12]

Fuzzy OWL Ø Extension of OWL Ø Example (describing the safety of a location): l l Without fuzzy, the location is either safe or not safe With fuzzy, the location is safe to a degree Ø Classes and properties are ‘fuzzy’ Ø A class is considered a fuzzy set [1] Ø A property is a fuzzy relation over a set [1]

Fuzzy OWL Ø Requires extension of to map OWL entailment to satisfiability [4] Ø Reasoning changes in that when concepts are represented as nodes in forest-like representations, a “membership degree” is associated with each node indicating it belongs to a concept [4] Ø Degrees added to OWL facts

Fuzzy OWL Taken from [4].

Probability Theory “. . the central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single occurrences or evolve over time in an apparently random fashion…” [11]

PR-OWL Ø Developed as an extension to OWL (basically an upper ontology) l Ø Uses MEBN logic rather than extending OWL l Ø Ø Represent conditional probability distribution [21] MFrags organized into MEBN Theories (MTheories) [21] l Ø A first order Bayesian logic [21] Consists of entities and attributes Attributes about entities and relationships to each other – MEBN fragments (MFrag) [21] l Ø Represents complex Bayesian models [21] Collectively satisfy consistency constraints [21] Goal l Provide a way to support Bayesian models

PR-OWL Taken from [21].

Bayes. OWL Ø Ø Ø Ø Ø Express OWL ontologies as Bayesian networks by means of rules For each node, a conditional probability table (CPT) is constructed [15] All subject and object classes translated into concept nodes [15] Arc drawn between 2 concept nodes if the 2 classes are related by predicate [15] Direction based on class hierarchy L-Nodes generated during translation to represent OWL logical operators True/false value for each node indicates whether the instance belongs to the concept CPTs are approximated using the “iterative proportional fitting procedure (IPFP)” [15] Restricted currently to OWL-DL taxonomies [15] Goals l l Support ontology reasoning using probabilistic approach Support ontology mapping

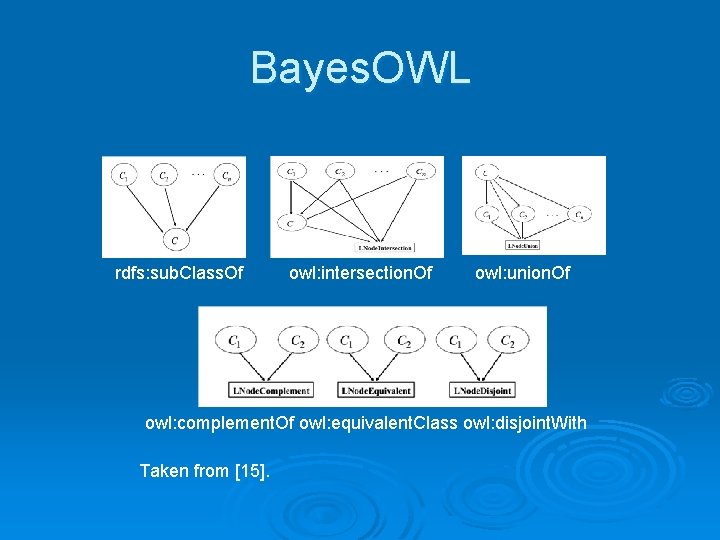
Bayes. OWL rdfs: sub. Class. Of owl: intersection. Of owl: union. Of owl: complement. Of owl: equivalent. Class owl: disjoint. With Taken from [15].

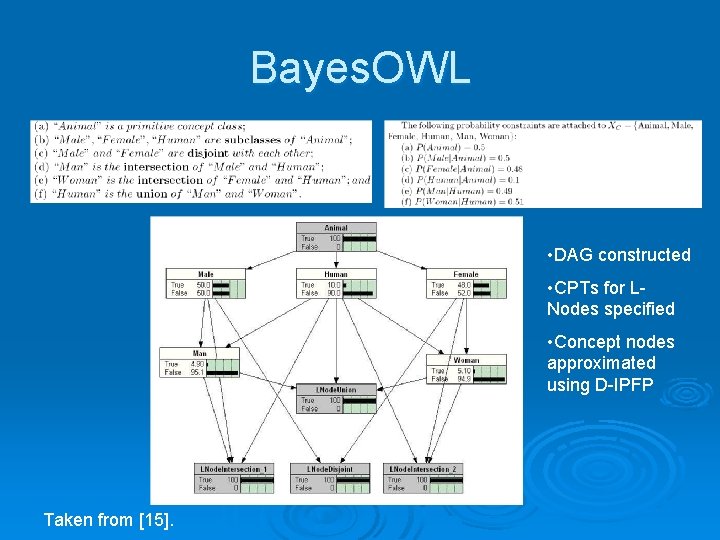
Bayes. OWL • DAG constructed • CPTs for LNodes specified • Concept nodes approximated using D-IPFP Taken from [15].

Bayes. OWL Ø Reasoning Support [15] l l l Concept satisfiability Concept overlapping Concept subsumption Ø Extensions to OWL to support probabilistic representation [15] l l Prior. Prob Cond. Prob Ø Concept Mapping [15]

Bayes. OWL Extensions to OWL Taken from [15].

Pronto Ø Ø Non-monotonic probabilistic DL reasoner Built on top of Pellet Uses P-SHIQ(D) formalism [8] Expressing uncertain axioms l Ø Probabilistic Reasoning l Ø Ø Ø Syntax based upon Lukasiewicz’s conditional constraints [8] Lehmann’s lexicographic entailment [8] Represents uncertain ontological knowledge and reasoning [8] Capable of representing uncertainty in both ABox and TBox axioms [8] “All inferences are done in a totally ‘logical’ way” (no translation) [8] Uses “OWL 1. 1 axiom annotations to associate probability intervals with uncertain OWL axioms” [8] Doesn’t scale beyond “ 15 generic (TBox) conditional constraints” [9]

Pronto Ø Conditional constraints l l l Ø (D|C)[l, u] C and D concepts in P-SHIQ(D) [l, u] closed interval within [0, 1] Supports overriding l l Can handle certain probabilistic conflicts Flying birds/penguin problem • Pronto allows “more specific constraints to override more generic ones” [9] • “if Pronto knows that Tweety is a Penguin and Penguin is a subclass-of Bird, it will override the constraint (Flying. Object|Bird)[0. 9; 1. 0] by (Flying. Object|Penguin)[0. 0; 0. 05] and correctly entail Tweety: (Flying. Object|owl: Thing)[0. 0; 0. 05]. “ [9]

Uncertainty and Ontologies Mapping Ø Mapping a problem l l Existing approaches - combination of syntactic and semantic measures [18], use machine learning, or linguistics and natural language processing [15] Quality varies depending upon domain [18] Wang argues without use of a thesaurus, inaccuracies will occur [22] Ø Problem: Ø l When mapping a concept from ontology A to ontology B there isn’t always a single concept match but rather a number of concepts that match to some degree

Uncertainty and Ontologies Mapping Ø A proposed truth theory solution based on the following [18]: l Dempster-Shafer, uncertain reasoning over potential mappings • Evidence Theory l l Ø Similarity matrix comparing all concepts/properties Similarity measure of a concept between O 1 and O 2 DS combines evidence learned to form new belief Promising approach Multi-agent ontology mapping framework [18] l l Not domain dependent Doesn’t require large amounts of training data

Uncertainty and Ontologies Mapping Ø A proposed solution by Wang [22]: l l ACAOM Uses Word. Net to calculate similarities for node names Name based mapping Instance strategy • More semantics more feasible to match • Documents assigned to nodes l Uses vector space models to rank matches

Uncertainty and Ontologies Mapping Ø Bayes. OWL [15] also proposed a solution l Argue that existing similarity approaches will not work • If degree of similarity is not present in both concepts being matched [15] • If concept itself is fuzzy [15] l l l Uses Bayes. OWL and belief propagation between BNs [15] Ontologies are first translated into BNs [15] Use probabilistic evidence reasoning to determine match [15]

Uncertainty and Ontologies – An Ontology of Uncertainty Proposed by the W 3 C UR 3 W-XG group Ø Provides a vocabulary for representing different types of uncertainty Ø Was a good start but refinement needed [20] Ø Strategy to use such an ontology as a way to drive a reasoner Ø l l Open issue: coordination of reasoning of different uncertainty models in knowledge base [19] Uses SWRL rules to assign uncertainty to each relation [19]

Uncertainty and Ontologies – An Ontology of Uncertainty Taken from [20].

Uncertainty and Web Services Service discovery – what is best service for request? Ø Matching goal to service Ø Brokers used for filtering Ø Semantic Web Service Framework Ø l l Semantic Web Service Language – concepts/descriptions [17] Semantic Web Service Ontology – conceptual model [17] It is argued that current frameworks use first order and description logics and “goal capabilities” are “based on subsumption checking or query-answering”[16] Ø Proposed approach uses Incident Calculus [16] Ø

Demo - Pronto Example: Breast Cancer Risk Models Ø Models 2 types of risks – absolute and relative Ø Combining risk factors to determine likelihood of breast cancer for a woman [8] Ø l Distinction between known and inferred Pronto uses an ontology for knowledge Ø Uses probabilistic statements to enable computable inferencing [8] Ø The probabilistic statements complement the OWL syntax Ø

Demo - Pronto Risk factors relevant to breast cancer are subclasses of ‘Risk. Factor’ Categories of women that have certain risk factors are subclasses of ‘Woman. With. Risk. Factors’ Ø Women with risk of developing cancer subclass ‘Woman. Under. BRCRisk’ Ø The goal: Ø Ø l l “Compute the probability that a certain woman is an instance of some Woman. Under. BRCRisk subclass given that she is an instance of some Woman. With. Risk. Factors subclass” [8] “Infer generic probabilistic subsumption between classes under Woman. Under. BRCRisk and under Woman. With. Risk. Factors” [8] Conditional constraints are used to represent ‘uncertain background knowledge’ using the OWL 1. 1 axiom annotations [8] Ø The demo defines constraints to “express how risk factors influence the risk of developing cancer” [8] Ø Pronto combines the factors and computes the probability that a woman is an instance of a subclass of ‘Woman. Under. BRCRisk’ Ø

Demo - Pronto <owl: Object. Property rdf: about="#has. Risk. Factor"> <rdfs: domain rdf: resource="#Person"/> <rdfs: range rdf: resource="#Risk. Factor"/> </owl: Object. Property> <owl: Class rdf: about="#Woman. Taking. Estrogen"> <owl: equivalent. Class> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk. Factor"/> <owl: some. Values. From rdf: resource="#Estrogen"/> </owl: Restriction> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. With. Risk. Factors"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk. Factor"/> <owl: some. Values. From rdf: resource="#Risk. Factor"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Aged. Under 50"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Age"/> <owl: some. Values. From rdf: resource="#Age. Under 50"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman. With. Risk. Factors"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. Absolute. BRCRisk"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#Absolute. BRCRisk"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. BRCRisk"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#BRCRisk"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. Increased. BRCRisk"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#Increased. BRCRisk"/> </owl: Restriction> <rdf: Description rdf: about="#Woman. Under. BRCRisk"/> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. Lifetime. BRCRisk"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#Lifetime. BRCRisk"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman. Under. Absolute. BRCRisk"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. Moderately. Increased. BRCRisk"> <owl: equivalent. Class> <owl: intersection. Of rdf: parse. Type="Collection"> <rdf: Description rdf: about="#Woman. Under. Increased. BRCRisk"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#Moderately. Increased. BRCRisk"/> </owl: Restriction> </owl: intersection. Of> </owl: Class> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman. Under. Increased. BRCRisk"/> <owl: disjoint. With rdf: resource="#Woman. Under. Strongly. Increased. BRCRisk"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto <owl: Class rdf: about="#Woman. Under. Moderately. Reduced. BRCRisk"> <owl: equivalent. Class> <owl: Restriction> <owl: on. Property rdf: resource="#has. Risk"/> <owl: some. Values. From rdf: resource="#Moderately. Reduced. BRCRisk"/> </owl: Restriction> </owl: equivalent. Class> <rdfs: sub. Class. Of rdf: resource="#Woman. Under. Reduced. BRCRisk"/> <owl: disjoint. With rdf: resource="#Woman. Under. Strongly. Reduced. BRCRisk"/> <owl: disjoint. With rdf: resource="#Woman. Under. Weakely. Reduced. BRCRisk"/> </owl: Class> Taken from http: //clarkparsia. com/pronto/cancer_ra. owl

Demo - Pronto   <owl 11: Axiom> <rdf: subject rdf: resource="#Woman"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Lifetime. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Lifetime. BRCRisk <pronto: certainty >0; 0. 123</pronto: certainty> > <pronto: certainty>0; 0. 123</ </owl 11: Axiom>  <owl 11: Axiom> <rdf: subject Woman. With. BRCAMutation"/> <rdf: subject rdf: resource="#Woman. With. BRCAMutation <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Lifetime. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Lifetime. BRCRisk <pronto: certainty >0. 3; 0. 85</pronto: certainty> > <pronto: certainty>0. 3; 0. 85</ </owl 11: Axiom>  <owl 11: Axiom> <rdf: subject rdf: resource="#Woman. With. BRCA 1 Mutation"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Lifetime. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Lifetime. BRCRisk <pronto: certainty >0. 6; 0. 8</pronto: certainty> > <pronto: certainty>0. 6; 0. 8</ </owl 11: Axiom> Taken from http: //clarkparsia. com/pronto/cancer_cc. owl

Demo - Pronto  <owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged. Under 20"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty >0; 0. 0005</pronto: certainty> > <pronto: certainty>0; 0. 0005</ </owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged 2030"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty>0; 0. 004</pronto: certainty> > < </owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged 3040"/> <rdf: predicate rdf: resource="& rdfs; sub. Class. Of"/> < rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty >0; 0. 014</pronto: certainty> > <pronto: certainty>0; 0. 014</ </owl 11: Axiom> Taken from http: //clarkparsia. com/pronto/cancer_cc. owl

Demo - Pronto <owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged 4050"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty >0; 0. 025</pronto: certainty> > <pronto: certainty>0; 0. 025</ </owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged 5060"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty>0; 0. 035</pronto: certainty> > < </owl 11: Axiom> <rdf: subject rdf: resource="#Woman. Aged 6070"/> <rdf: predicate rdfs; sub. Class. Of"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of <rdf: object Woman. Under. Short. Term. BRCRisk"/> <rdf: object rdf: resource="#Woman. Under. Short. Term. BRCRisk <pronto: certainty >0; 0. 039</pronto: certainty> > <pronto: certainty>0; 0. 039</ </owl 11: Axiom> Taken from http: //clarkparsia. com/pronto/cancer_cc. owl

Demo - Pronto  Taken from http: //clarkparsia. com/pronto/cancer_cc. owl

Demo - Pronto <owl 11: Axiom> <rdf: subject rdf: resource="#Helen"/> <rdf: predicate rdf: resource="& rdf; type"/> < rdf: resource="&rdf; type <rdf: object Postmenopausal. Woman"/> <rdf: object rdf: resource="#Postmenopausal. Woman <pronto: certainty >1; 1</pronto: certainty> > <pronto: certainty>1; 1</ </owl 11: Axiom> <rdf: subject rdf: resource="#Helen"/> <rdf: predicate rdf; type"/> <rdf: predicate rdf: resource="&rdf; type <rdf: object Woman. Taking. Estrogen"/> <rdf: object rdf: resource="#Woman. Taking. Estrogen <pronto: certainty>1; 1</pronto: certainty> > < </owl 11: Axiom> <rdf: subject rdf: resource="#Helen"/> <rdf: predicate rdf; type"/> <rdf: predicate rdf: resource="&rdf; type <rdf: object Woman. Taking. Progestin"/> <rdf: object rdf: resource="#Woman. Taking. Progestin <pronto: certainty >1; 1</pronto: certainty> > <pronto: certainty>1; 1</ </owl 11: Axiom> Taken from http: //clarkparsia. com/pronto/cancer_cc. owl

Demo - Pronto <owl 11: Axiom> <rdf: subject rdf: resource="#Ashkenazi. Jewish. Woman"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of"/> <rdf: object rdf: resource="#Woman. With. BRCAMutation"/> <pronto: certainty>0. 025; 0. 025</pronto: certainty> </owl 11: Axiom> <rdf: subject rdf: resource="#Woman. With. BRCAMutation"/> <rdf: predicate rdf: resource="&rdfs; sub. Class. Of"/> <rdf: object rdf: resource="#Woman. Under. Lifetime. BRCRisk"/> <pronto: certainty>0. 3; 0. 85</pronto: certainty> </owl 11: Axiom>

Demo - Pronto Ø Running query (generic TBox conditional constraint) (C|D)[l, u] [9] entail http: //clarkparsia. com/pronto/cancer_ra. ow l#Ashkenazi. Jewish. Woman http: //clarkparsia. com/pronto/cancer_ra. ow l#Woman. Under. Lifetime. BRCRisk

Demo - Pronto Query : entail Result: 34: (Woman. Under. Lifetime. BRCRisk|Ashkenazi. Jewish. Woman)[0. 0075; 0. 123] Explanation: Explaining the generic constraint 34: (Woman. Under. Lifetime. BRCRisk|Ashkenazi. Jewish Woman)[0. 0075; 0. 123]: Lower bound is because of: [[8: (Woman. With. BRCAMutation|Ashkenazi. Jewish. Woman)[0. 025; 0. 025], 7: (Woman. Under. Li fetime. BRCRisk|Woman. With. BRCAMutation)[0. 3; 0. 85]]] Upper bound is because of: [[10: (Woman. Under. Lifetime. BRCRisk|Woman)[0. 0; 0. 123]]] Result computed in 6266 ms

Want to learn more? Ø Attend the 2009 URSW Conference l Ø Visit W 3 C Uncertainty Reasoning for the World Wide Web Incubator Group l Ø http: //c 4 i. gmu. edu/ursw/2008/ Download Pronto l Ø http: //www. w 3. org/2005/Incubator/urw 3/ Review presentations from last year’s conference l Ø http: //c 4 i. gmu. edu/ursw/2009/ http: //pellet. owldl. com/pronto/ Download Fi. RE l http: //www. image. ece. ntua. gr/~nsimou/Fi. RE/

References [1] - Stoilos, Simou, Stamou, Kollias, “Uncertainty and the Semantic Web”, http: //www. image. ece. ntua. gr/php/savepaper. php? id=445, 2006, IEEE [2] – 2008 Conference, “Uncertainty Reasoning for the Semantic Web”, http: //c 4 i. gmu. edu/ursw/2008/index. html [3] - 2007 Conference, “Uncertainty Reasoning for the Semantic Web”, http: //c 4 i. gmu. edu/ursw/2007/index. html [4] - Stoilos, Stamou, Tzouvaras, Pan, Horrocks, “Fuzzy OWL: Uncertainty and the Semantic Web”, http: //www. image. ntua. gr/papers/398. pdf [5] - Lassila, “Some Personal Thoughts on Semantic Web and “Non-symbolic” AI”, http: //c 4 i. gmu. edu/ursw/2008/talks/URSW 2008_Keynote_Lassila. pdf, 2008, ISWC [6] – Williams, Bastin, Cornford, Ingram, “Describing and Communicating Uncertainty within the Semantic Web”, http: //c 4 i. gmu. edu/ursw/2008/papers/URSW 2008_F 3_Williams. Et. Al. pdf [7] – Sanchez, “Fuzzy logic and semantic web”, http: //books. google. com/books? id =Cidej 8 b 4 ESIC&pg=PA 4&lpg=PA 4&dq=monotonic+bivalent+language&source= =bl&ots=mtb. Zc. Zfa. O 7&sig=Vt. Gq. KXuhttp: //books. google. com/books? id=Cidej 8 b 4 ESIC&pg=PA 4&lpg=PA 4&dq= bl&ots=mtb. Zc. Zfa. O 7&sig=Vt. Gq. KXurrzl 5 HOw 36 UBTe. Tpdo. E&hl=en&ei =s. BIASpu. JFon. Itge. Knpy. TBw&sa= rrzl 5 HOw 36 UBTe. Tpdo. E&hl=en&ei= s. BIASpu. JFon. Itge. Knpy. TBw&sa=X&oi=book_result&ct=result&resnum=1#PPP 1, M 1 [8] – Klinov, Parsia, “Demonstrating Pronto: a Non-monotonic Probabilistic OWL Reasoner”, http: //www. webont. org/owled/2008 dc/papers/owled 2008 dc_paper_2. pdf [9] – Klinov, “Introducing Pronto: Probabilistic DL Reasoning in Pellet“, http: //clarkparsia. com/weblog/2007/09/27/introducing-pronto/ [10] – Wikipedia Fuzzy Set theory, http: //en. wikipedia. org/wiki/Fuzzy_set [11] – Wikipedia Probability Theory, http: //en. wikipedia. org/wiki/Probability_theory [12] – Straccia, “A Fuzzy Description Logic for the Semantic Web”, http: //www. win. tue. nl/~aserebre/ks/Lit/Straccia 2006. pdf [13] – Mazzieri, Dragoni, “A Fuzzy Semantics for Semantic Web Languages”, http: //ftp. informatik. rwth-aachen. de/Publications/CEUR-WS/Vol-173/paper 2. pdf [14] – Wikipedia Description Logic, http: //en. wikipedia. org/wiki/Description_logic [15] – Ding, Peng, Pan, “Bayes. OWL: : Uncertainty Modeling in Semantic Web Ontologies”, http: //ebiquity. umbc. edu/_file_directory_/papers/217. pdf [16] – Martin-recurerda 1, Robertson 2, “Discovery and Uncertainty in Semantic Web Services”, http: //ftp. informatik. rwth-aachen. de/Publications/CEUR-WS/Vol 173/paper 4. pdf [17] – “Semantic Web Services Framework (SWSF) Overview”, http: //www. w 3. org/Submission/SWSF/ [18] – Nagy, Vargas-Vera, Motta, “Uncertain Reasoning for Creating Ontology Mapping on the Semantic Web”, http: //c 4 i. gmu. edu/ursw/2007/files/papers/URSW 2007_P 2_Nagy. Vera. Motta. pdf [19] – Ceravolo, Damiani, Leida, “Which Role for an Ontology of Uncertainty? ”, http: //c 4 i. gmu. edu/ursw/2008/papers/URSW 2008_P 6_Ceravolo. Et. Al. pdf [20] – Laskey, “Uncertainty Reasoning for the World Wide Web: Report on the URW 3 -XG Incubator Group”, http: //c 4 i. gmu. edu/ursw/2008/papers/URSW 2008_FX_Laskey. pdf [21] – Costa, Laskey, “PR-OWL: A Framework for Probabilistic Ontologies”, http: //volgenau. gmu. edu/~klaskey/papers/FOIS 2006_Costa. Laskey. pdf [22] – Wang, “Integrating Uncertainty Into Ontology Mapping”, http: //iswc 2007. semanticweb. org/papers/955. pdf