UNBONDED POSTTENSIONING SEISMIC APPLICATIONS IN CONCRETE STRUCTURAL WALLS

UNBONDED POST-TENSIONING: SEISMIC APPLICATIONS IN CONCRETE STRUCTURAL WALLS Yahya C. Kurama University of Notre Dame, Indiana, U. S. A Tokyo Institute of Technology Yokohama, Japan August 16, 2000
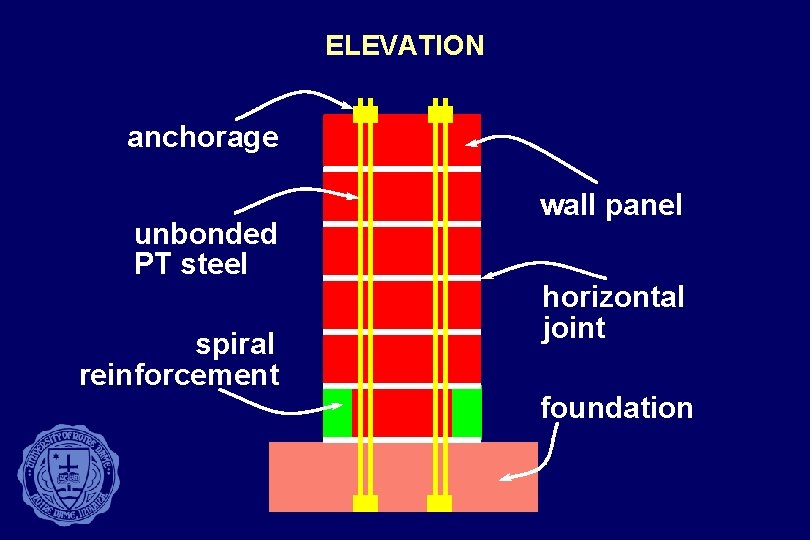
ELEVATION anchorage unbonded PT steel spiral reinforcement wall panel horizontal joint foundation
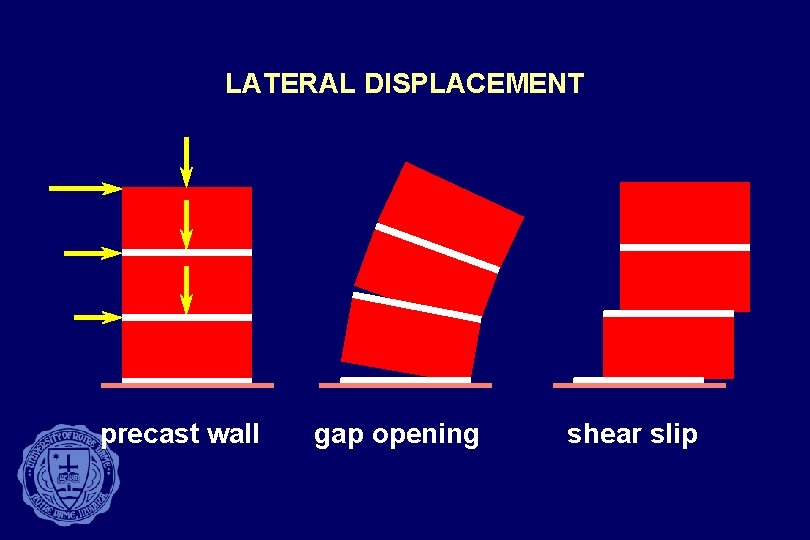
LATERAL DISPLACEMENT precast wall gap opening shear slip
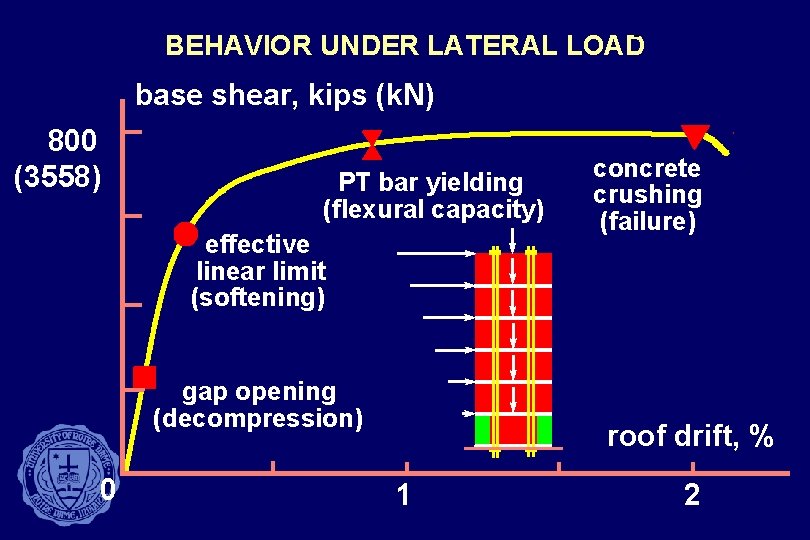
BEHAVIOR UNDER LATERAL LOAD base shear, kips (k. N) 800 (3558) PT bar yielding (flexural capacity) effective linear limit (softening) gap opening (decompression) 0 concrete crushing (failure) roof drift, % 1 2
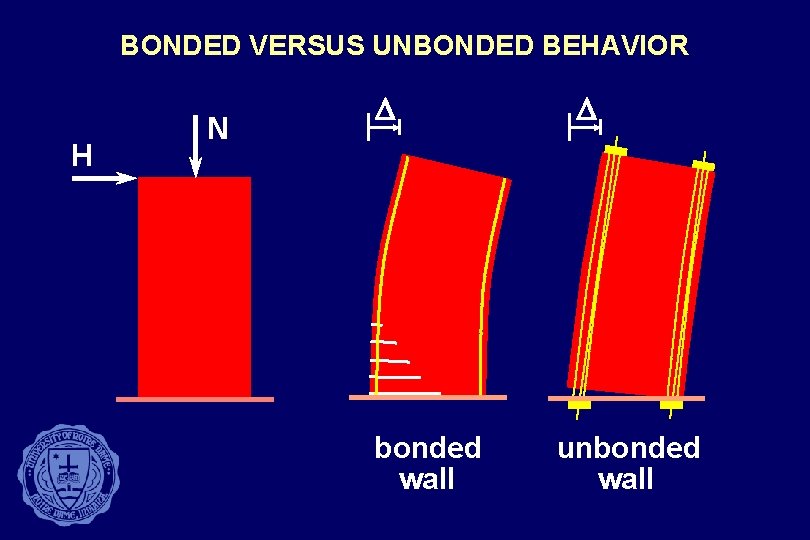
BONDED VERSUS UNBONDED BEHAVIOR H N D bonded wall D unbonded wall
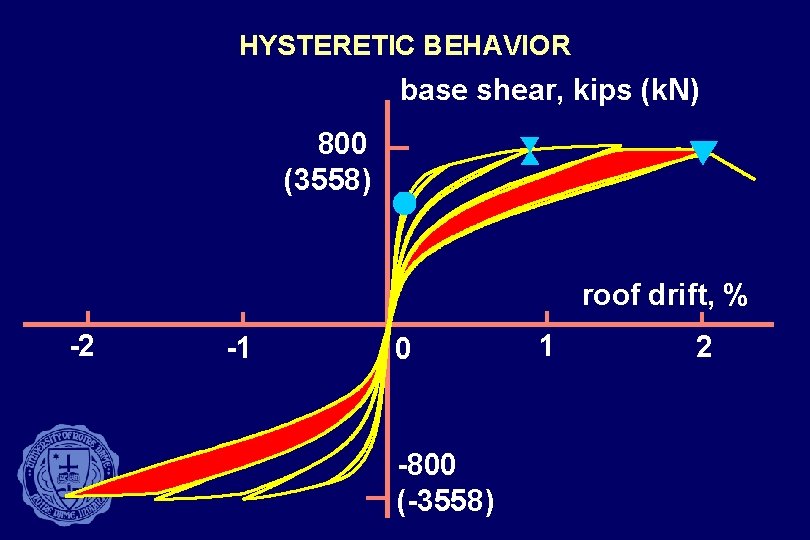
HYSTERETIC BEHAVIOR base shear, kips (k. N) 800 (3558) roof drift, % -2 -1 0 -800 (-3558) 1 2

OUTLINE • Unbonded post-tensioned precast walls – without supplemental damping – with supplemental damping • Unbonded post-tensioned hybrid coupled walls

UNBONDED POST-TENSIONED WALLS WITHOUT SUPPLEMENTAL ENERGY DISSIPATION Analytical Modeling
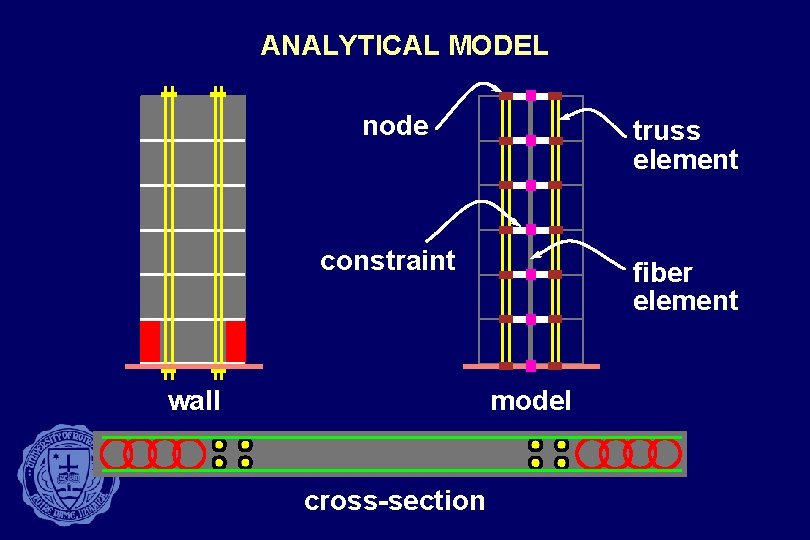
ANALYTICAL MODEL node truss element constraint fiber element wall model cross-section
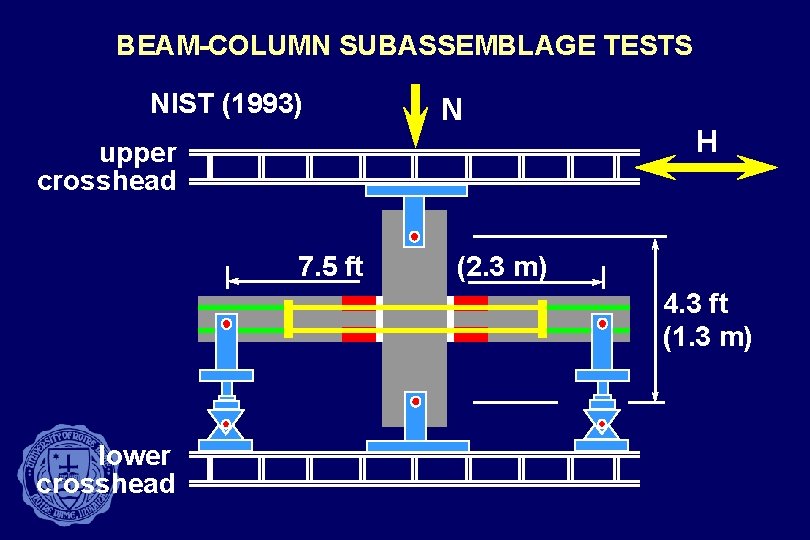
BEAM-COLUMN SUBASSEMBLAGE TESTS NIST (1993) N upper crosshead 7. 5 ft H (2. 3 m) 4. 3 ft (1. 3 m) lower crosshead
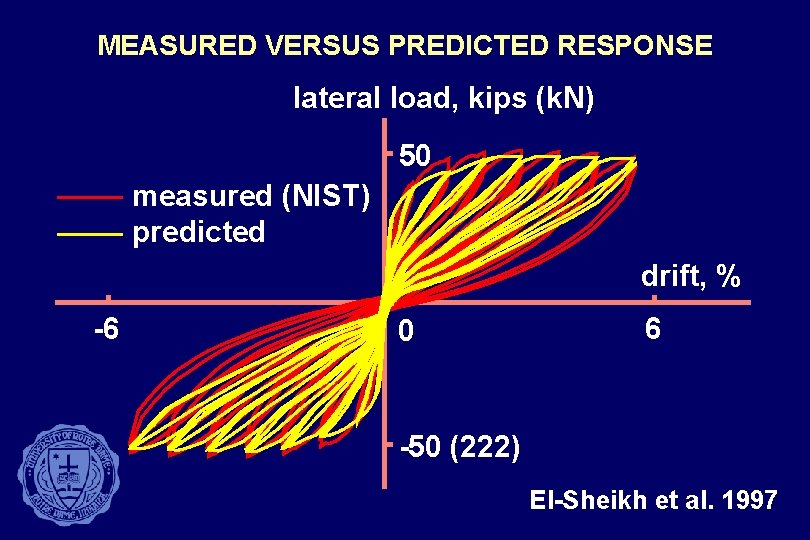
MEASURED VERSUS PREDICTED RESPONSE lateral load, kips (k. N) 50 measured (NIST) predicted drift, % -6 0 6 -50 (222) El-Sheikh et al. 1997
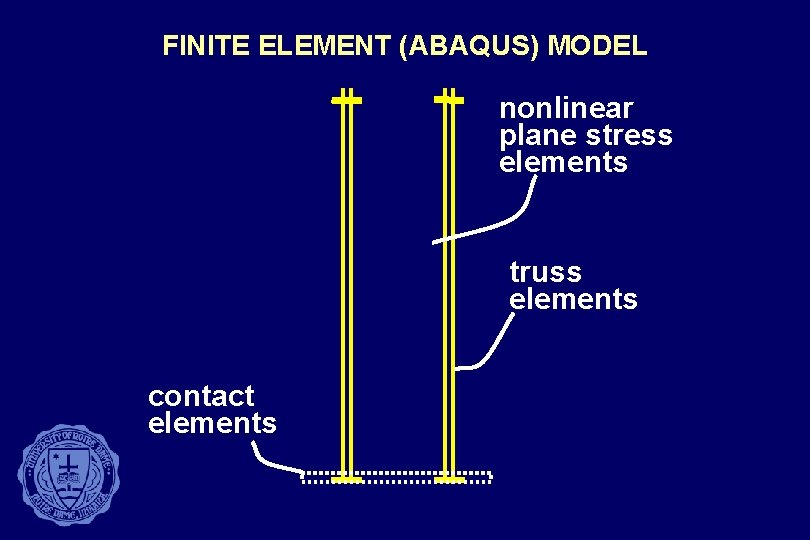
FINITE ELEMENT (ABAQUS) MODEL nonlinear plane stress elements truss elements contact elements

GAP OPENING
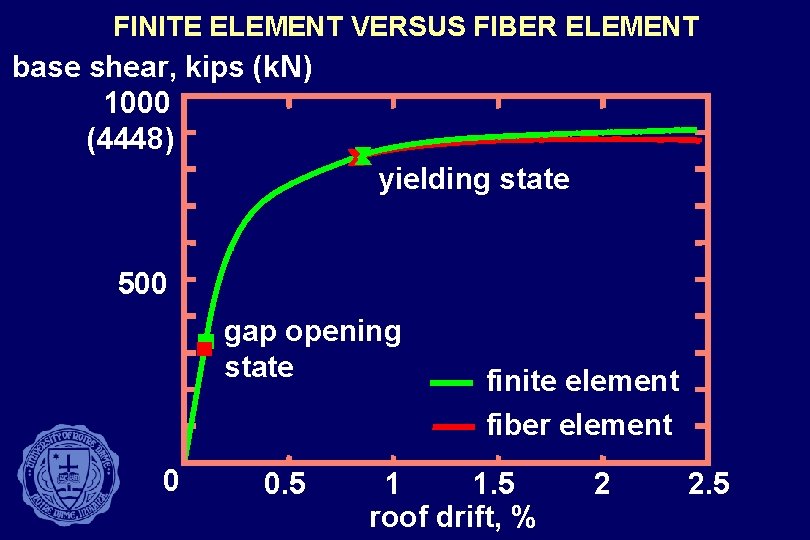
FINITE ELEMENT VERSUS FIBER ELEMENT base shear, kips (k. N) 1000 (4448) yielding state 500 gap opening state 0 0. 5 finite element fiber element 1 1. 5 roof drift, % 2 2. 5

Seismic Design and Response Evaluation
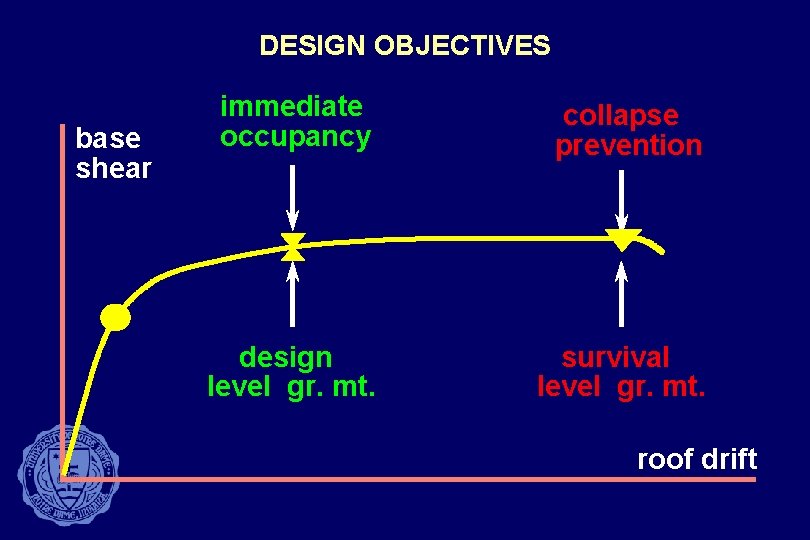
DESIGN OBJECTIVES base shear immediate occupancy collapse prevention design level gr. mt. survival level gr. mt. roof drift
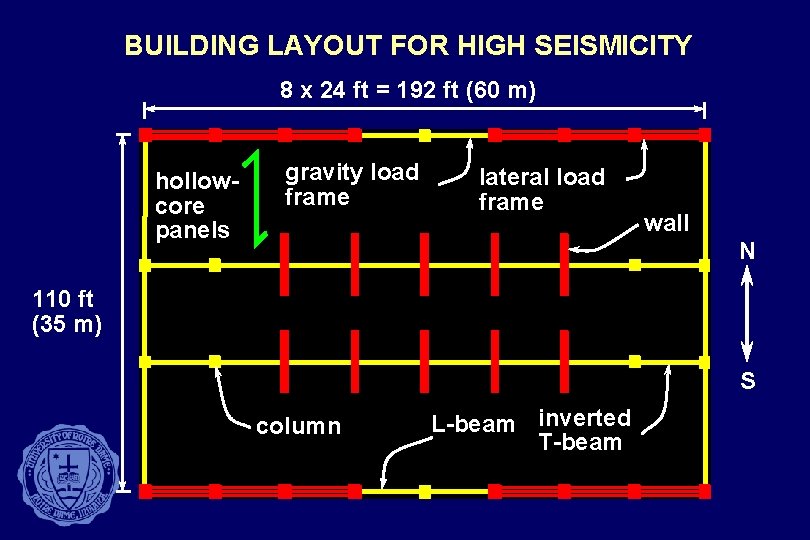
BUILDING LAYOUT FOR HIGH SEISMICITY 8 x 24 ft = 192 ft (60 m) hollowcore panels gravity load frame lateral load frame wall N 110 ft (35 m) S column L-beam inverted T-beam
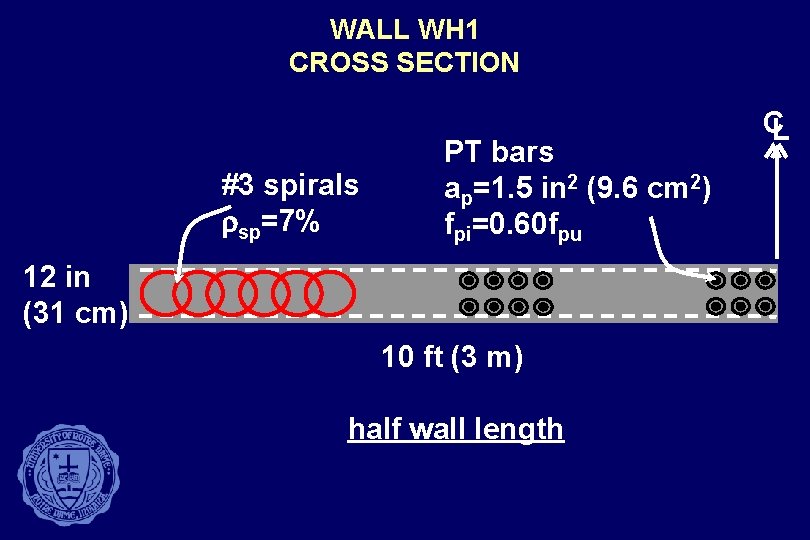
WALL WH 1 CROSS SECTION #3 spirals rsp=7% PT bars ap=1. 5 in 2 (9. 6 cm 2) fpi=0. 60 fpu 12 in (31 cm) 10 ft (3 m) half wall length CL
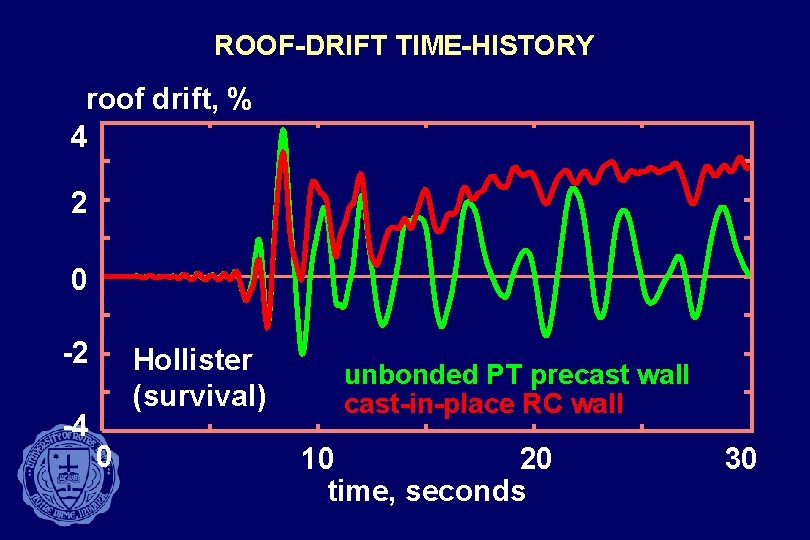
ROOF-DRIFT TIME-HISTORY roof drift, % 4 2 0 -2 -4 Hollister (survival) 0 unbonded PT precast wall cast-in-place RC wall 10 20 time, seconds 30

WALLS WITH SUPPLEMENTAL ENERGY DISSIPATION U. S. National Science Foundation CMS 98 -74872 CAREER Program
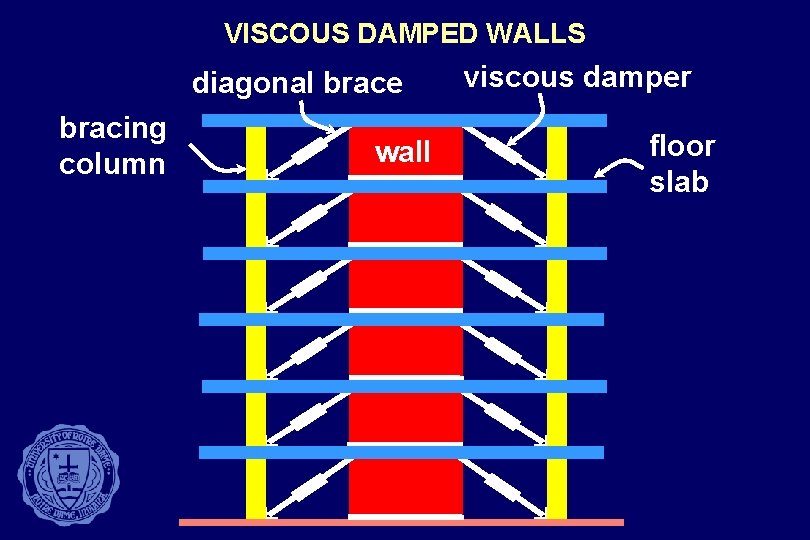
VISCOUS DAMPED WALLS diagonal brace bracing column wall viscous damper floor slab
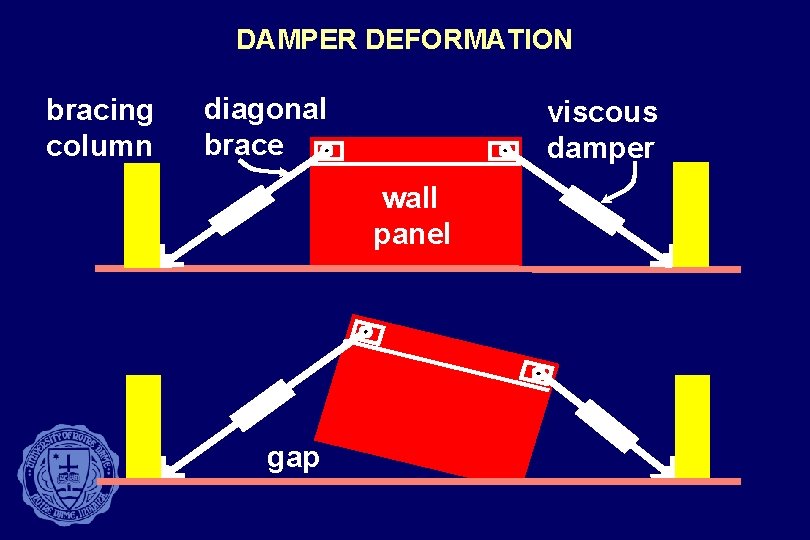
DAMPER DEFORMATION bracing column diagonal brace viscous damper wall panel gap
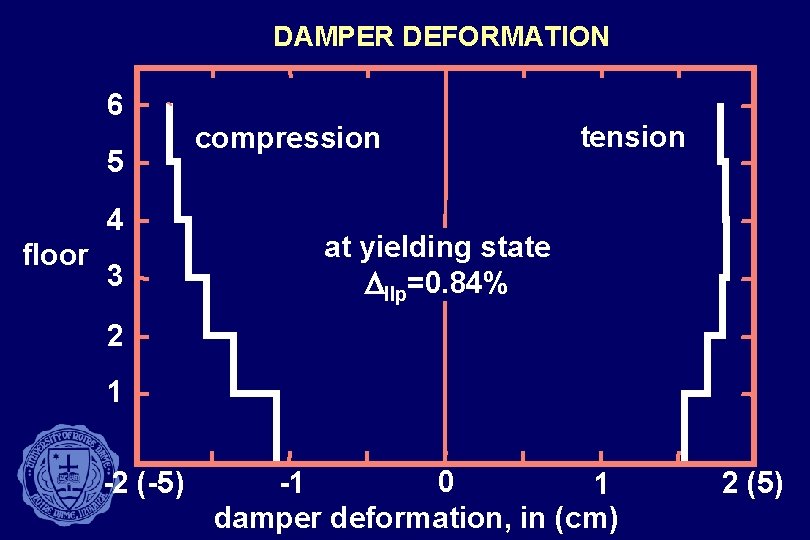
DAMPER DEFORMATION 6 5 4 floor 3 compression tension at yielding state Dllp=0. 84% 2 1 -2 (-5) 0 -1 1 damper deformation, in (cm) 2 (5)
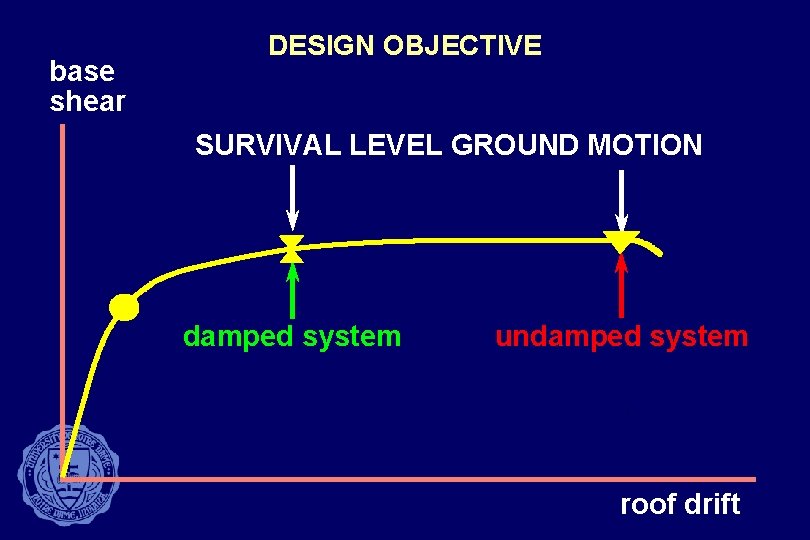
base shear DESIGN OBJECTIVE SURVIVAL LEVEL GROUND MOTION damped system undamped system roof drift
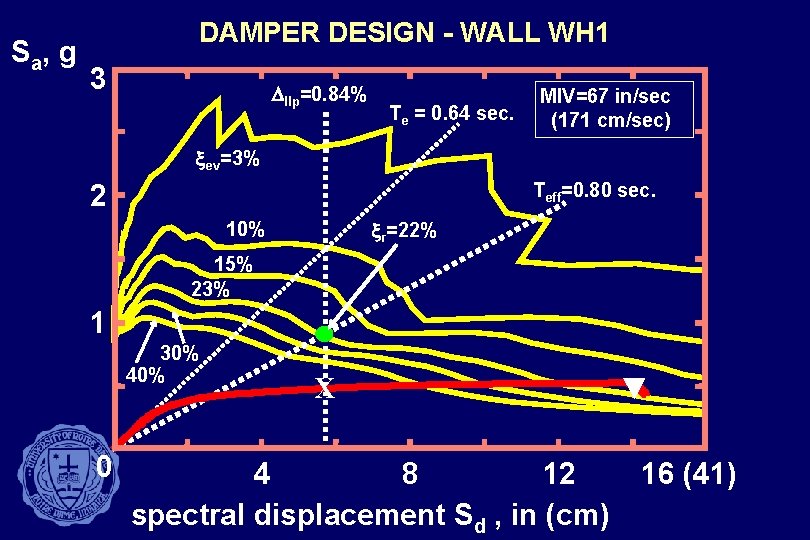
S a, g DAMPER DESIGN - WALL WH 1 3 Dllp=0. 84% Te = 0. 64 sec. MIV=67 in/sec (171 cm/sec) xev=3% 2 Teff=0. 80 sec. xr=22% 10% 15% 23% 1 30% 40% 0 X 4 8 12 spectral displacement Sd , in (cm) 16 (41)
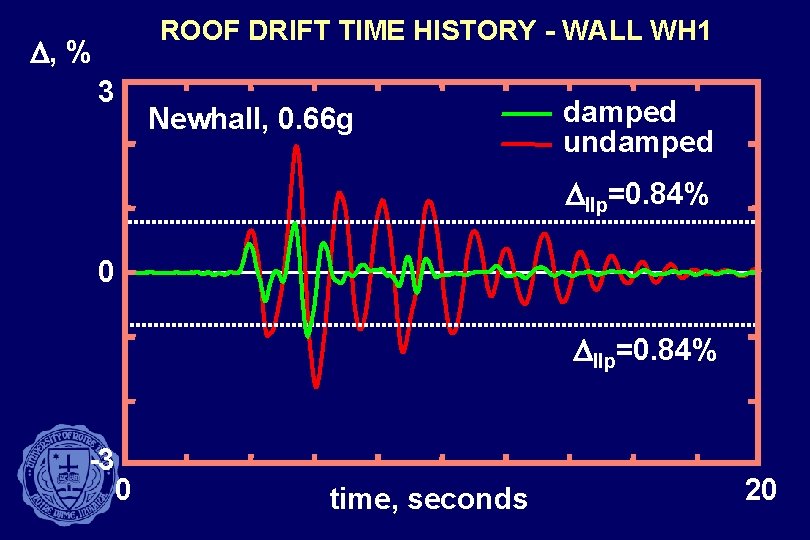
ROOF DRIFT TIME HISTORY - WALL WH 1 D, % 3 Newhall, 0. 66 g damped undamped Dllp=0. 84% 0 Dllp=0. 84% -3 0 time, seconds 20
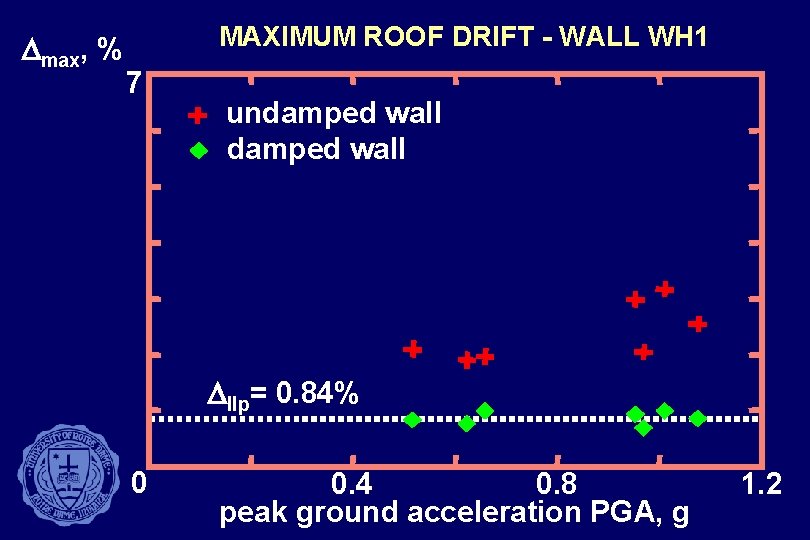
Dmax, % MAXIMUM ROOF DRIFT - WALL WH 1 7 undamped wall Dllp= 0. 84% 0 0. 4 0. 8 peak ground acceleration PGA, g 1. 2
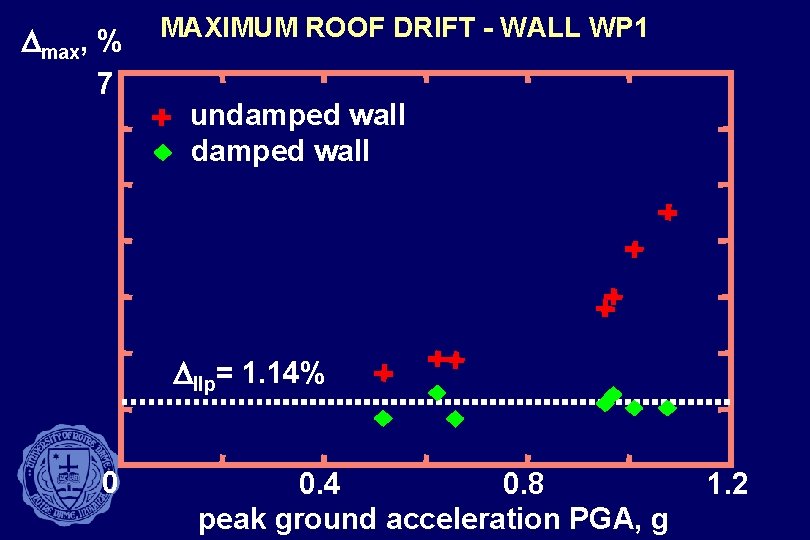
Dmax, % 7 MAXIMUM ROOF DRIFT - WALL WP 1 undamped wall Dllp= 1. 14% 0 0. 4 0. 8 peak ground acceleration PGA, g 1. 2

Dmax, % 7 MAXIMUM ROOF DRIFT - WALL WP 2 undamped wall Dllp= 1. 47% 0 0. 4 0. 8 peak ground acceleration PGA, g 1. 2
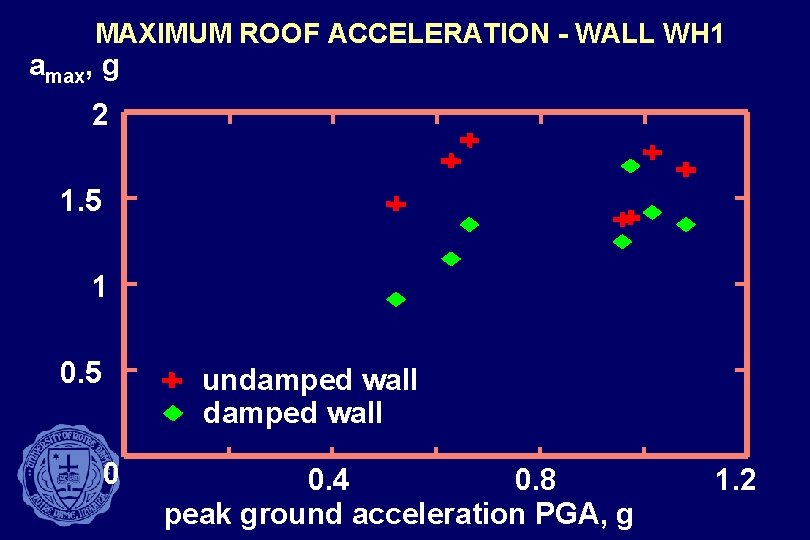
MAXIMUM ROOF ACCELERATION - WALL WH 1 amax, g 2 1. 5 1 0. 5 undamped wall 0 0. 4 0. 8 peak ground acceleration PGA, g 1. 2

UNBONDED POST-TENSIONED HYBRID COUPLED WALL SYSTEMS U. S. National Science Foundation CMS 98 -10067 U. S. -Japan Cooperative Program on Composite and Hybrid Structures
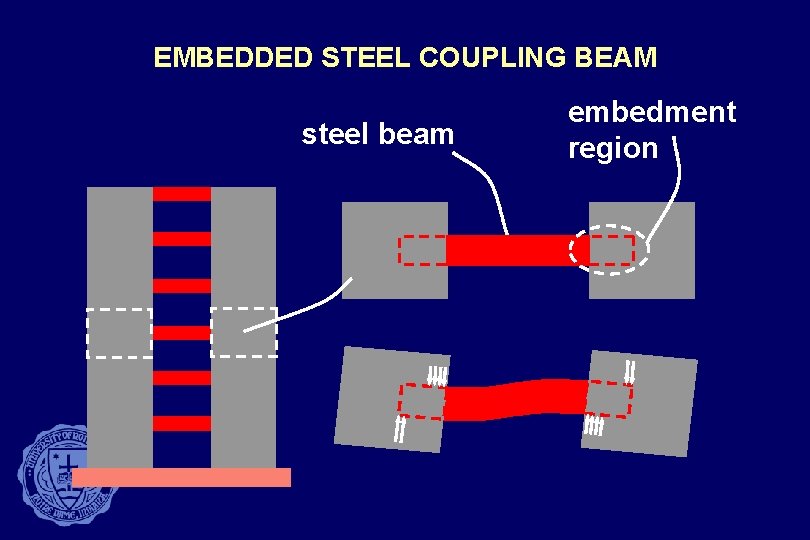
EMBEDDED STEEL COUPLING BEAM steel beam embedment region

TEST RESULTS FOR EMBEDDED BEAMS Harries et al. 1997
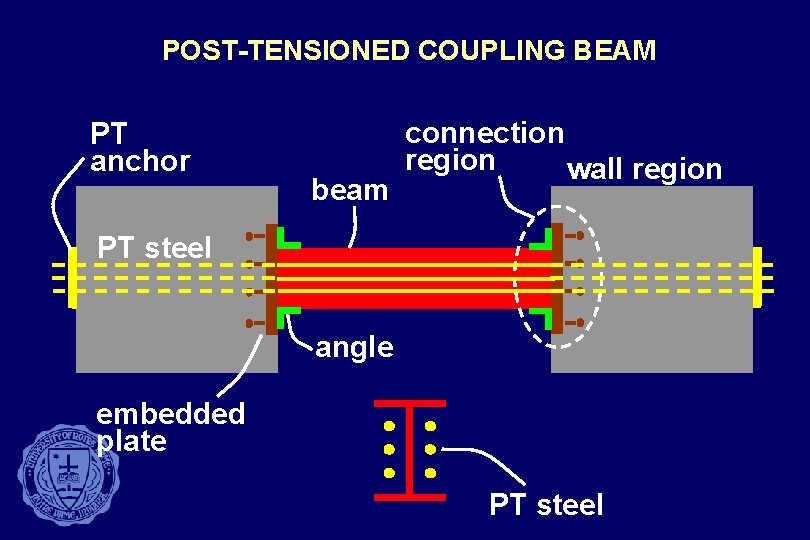
POST-TENSIONED COUPLING BEAM PT anchor beam connection region wall region PT steel angle embedded plate PT steel
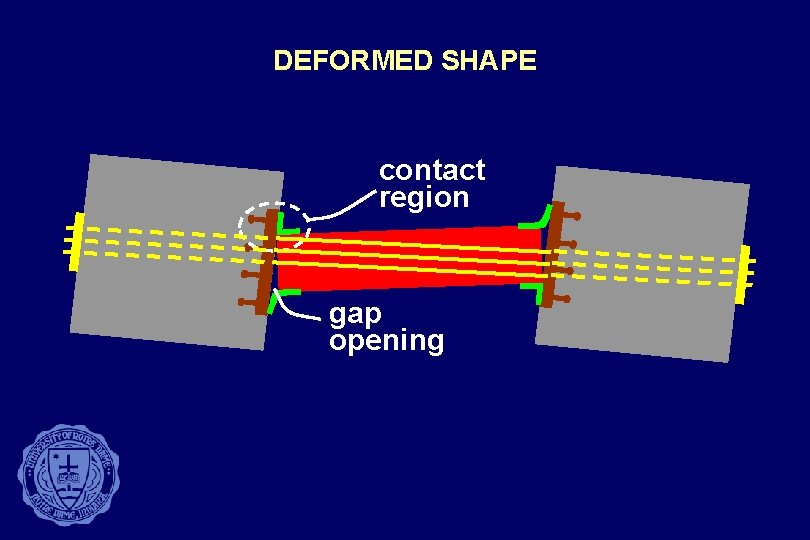
DEFORMED SHAPE contact region gap opening
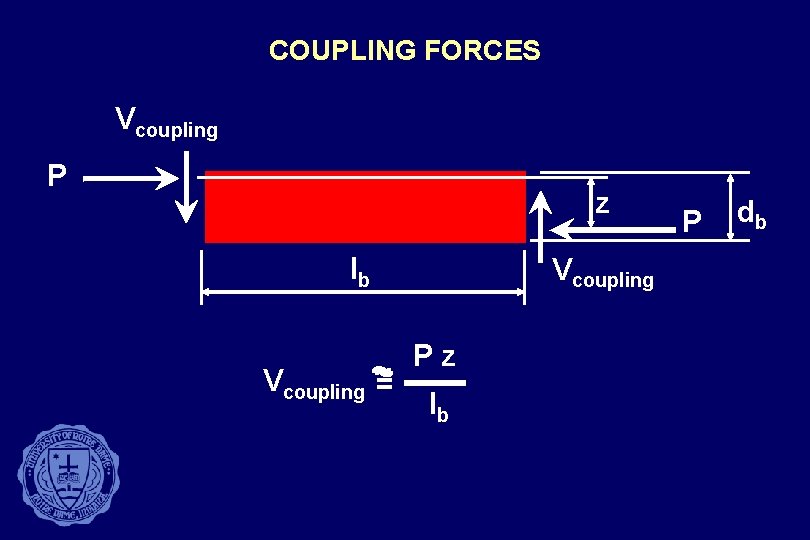
COUPLING FORCES Vcoupling P z lb Vcoupling = Vcoupling Pz lb P db

RESEARCH ISSUES • Force/deformation capacity of beam-wall connection region – beam – angle • Yielding of the PT steel • Energy dissipation • Self-centering • Overall/local stability
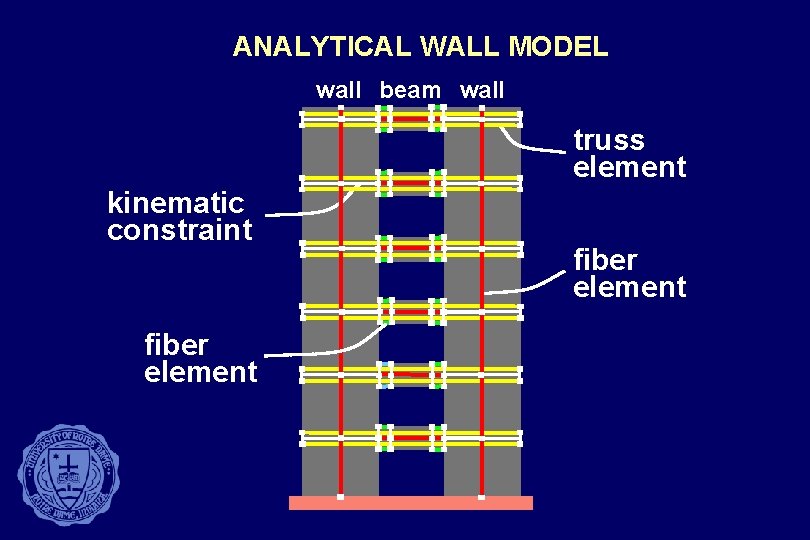
ANALYTICAL WALL MODEL wall beam wall truss element kinematic constraint fiber element
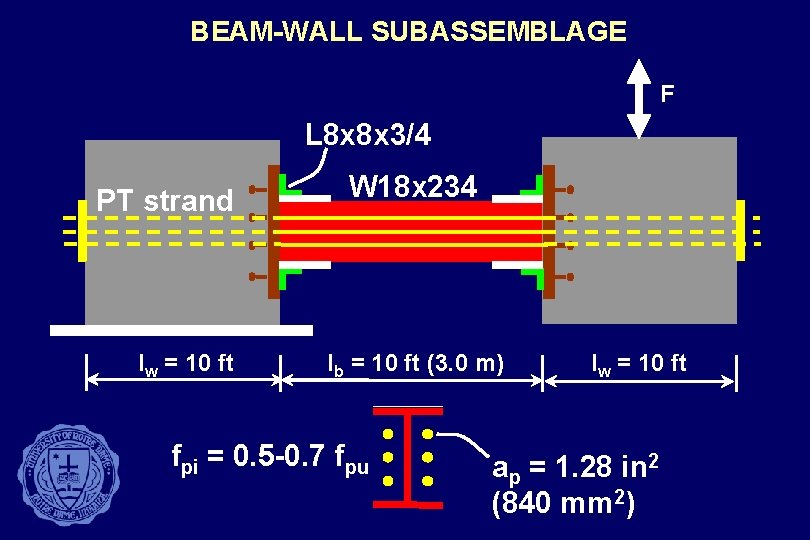
BEAM-WALL SUBASSEMBLAGE F L 8 x 8 x 3/4 PT strand lw = 10 ft W 18 x 234 lb = 10 ft (3. 0 m) fpi = 0. 5 -0. 7 fpu lw = 10 ft ap = 1. 28 in 2 (840 mm 2)
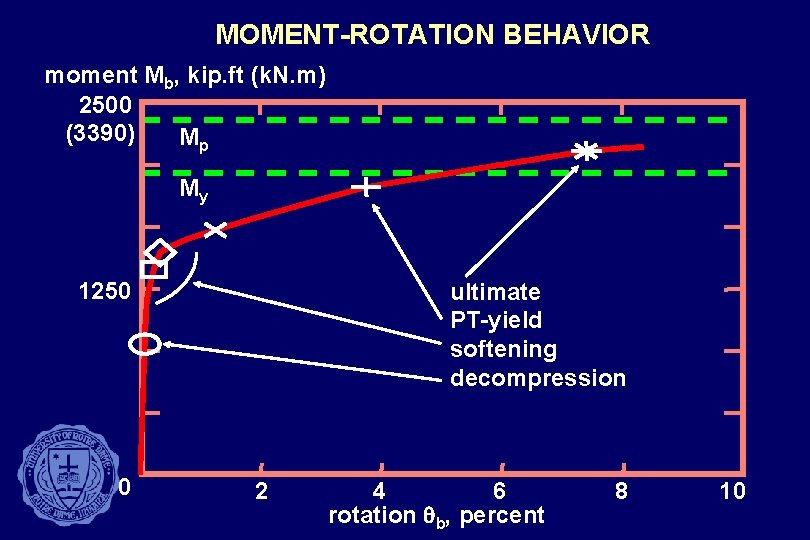
MOMENT-ROTATION BEHAVIOR moment Mb, kip. ft (k. N. m) 2500 (3390) Mp My 1250 0 ultimate PT-yield softening decompression 2 4 6 rotation qb, percent 8 10
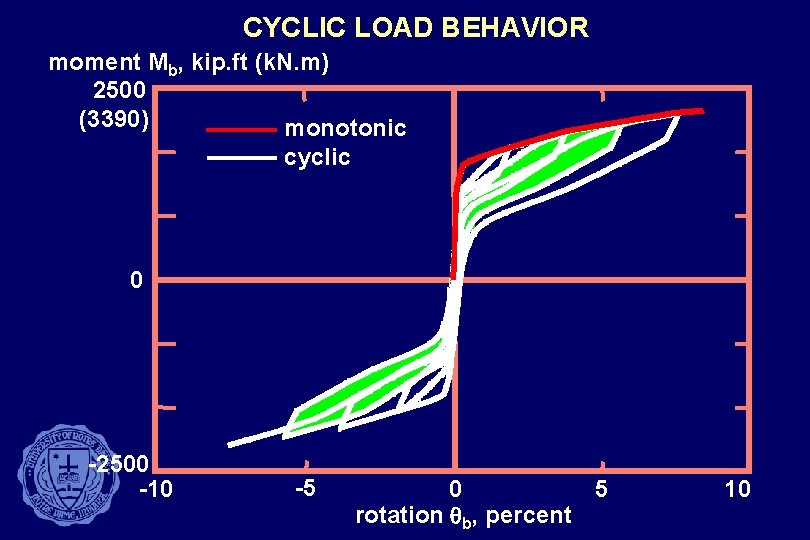
CYCLIC LOAD BEHAVIOR moment Mb, kip. ft (k. N. m) 2500 (3390) monotonic cyclic 0 -2500 -10 -5 0 5 rotation qb, percent 10
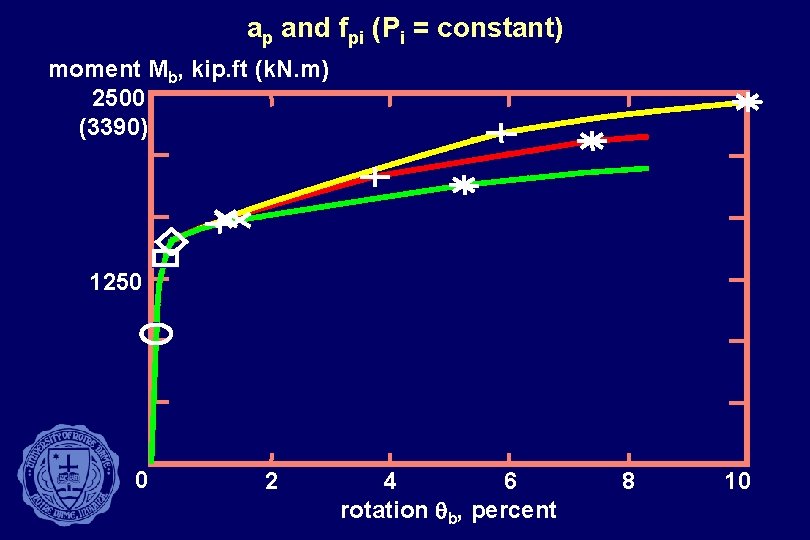
ap and fpi (Pi = constant) moment Mb, kip. ft (k. N. m) 2500 (3390) 1250 0 2 4 6 rotation qb, percent 8 10
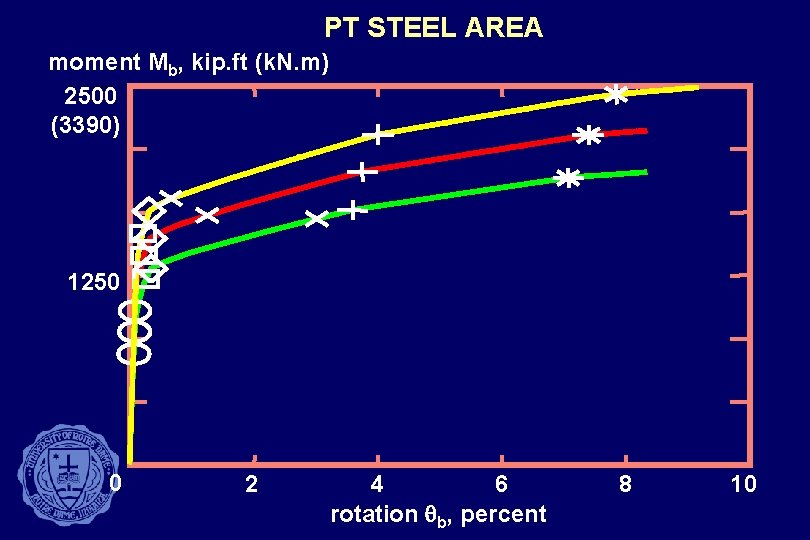
PT STEEL AREA moment Mb, kip. ft (k. N. m) 2500 (3390) 1250 0 2 4 6 rotation qb, percent 8 10
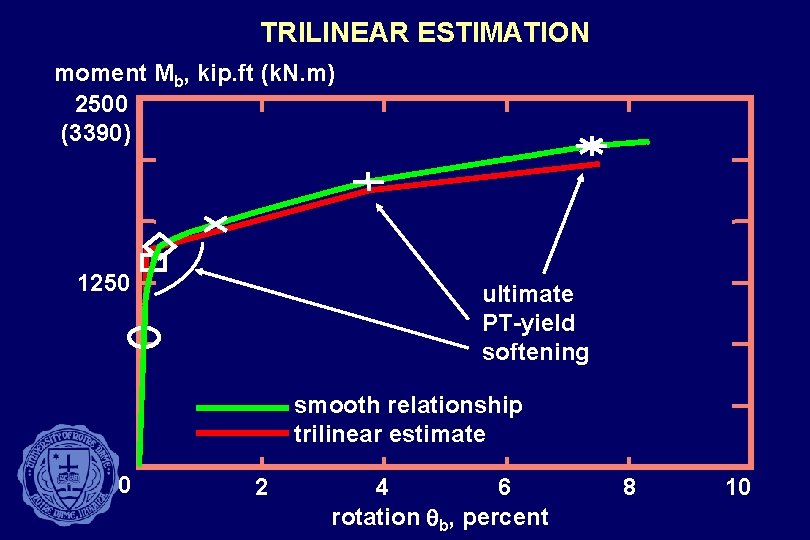
TRILINEAR ESTIMATION moment Mb, kip. ft (k. N. m) 2500 (3390) 1250 ultimate PT-yield softening smooth relationship trilinear estimate 0 2 4 6 rotation qb, percent 8 10
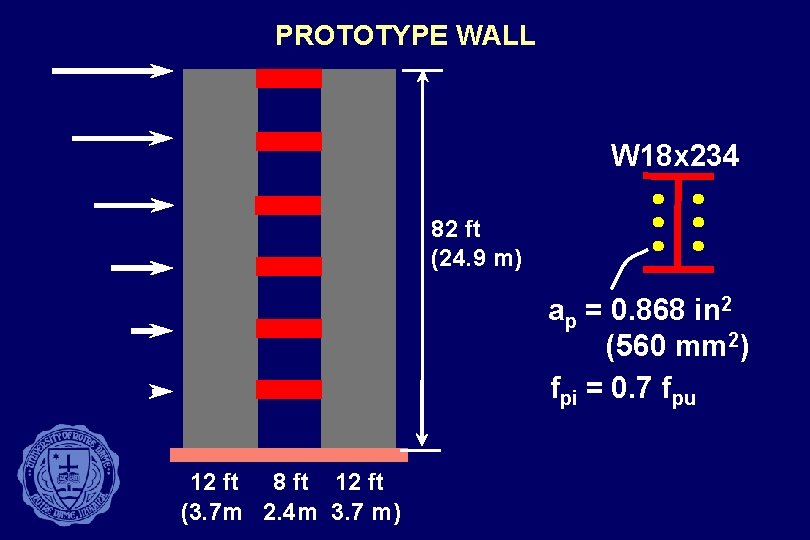
PROTOTYPE WALL W 18 x 234 82 ft (24. 9 m) ap = 0. 868 in 2 (560 mm 2) fpi = 0. 7 fpu 12 ft 8 ft 12 ft (3. 7 m 2. 4 m 3. 7 m)
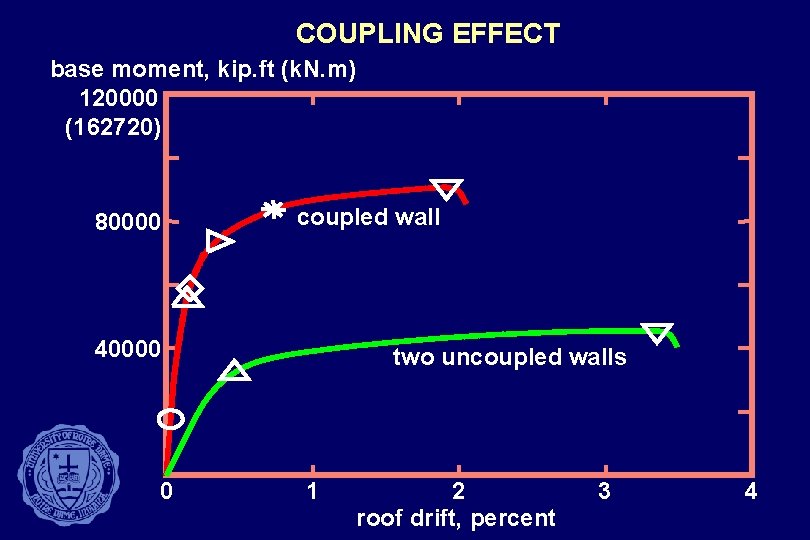
COUPLING EFFECT base moment, kip. ft (k. N. m) 120000 (162720) 80000 coupled wall 40000 0 two uncoupled walls 1 2 roof drift, percent 3 4

EXPERIMENTAL PROGRAM • Beam-wall connection subassemblages • Ten half-scale tests Objectives • Investigate beam M-q behavior • Verify analytical model • Verify design tools and procedures
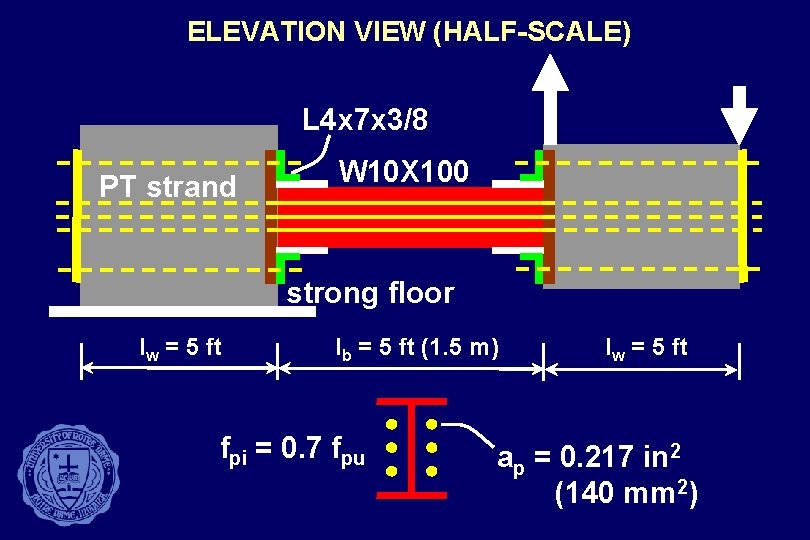
ELEVATION VIEW (HALF-SCALE) L 4 x 7 x 3/8 PT strand W 10 X 100 strong floor lw = 5 ft lb = 5 ft (1. 5 m) fpi = 0. 7 fpu lw = 5 ft ap = 0. 217 in 2 (140 mm 2)

CONCLUSIONS • Unbonded post-tensioning is a feasible construction method for reinforced concrete walls in seismic regions • Large self-centering capability • Softening, thus, period elongation • Small inelastic energy dissipation • Need supplemental energy dissipation in high seismic regions

http: //www. nd. edu/~concrete
- Slides: 50