Unbalanced Assignment Model Lecture 24 By Dr Arshad

Unbalanced Assignment Model Lecture 24 By Dr. Arshad Zaheer

RECAP q Assignment Model (Maximization) q Hungarian Method q Steps Involved q. Illustrations q Optimal Assignment

Unbalanced Assignment Problem Case 1 This is the case when the total number of machines exceeds total number of jobs. In this case, introduce required number of fictitious or dummy jobs at ‘ 0’ cost or at the cost stated in the problem to get the balanced assignment problem. Then use the assignment technique to obtain the optimal assignment. The fictitious or dummy jobs assigned to the machines mean that the corresponding machine will not be assigned any job.

Unbalanced Assignment Problem Case 2 This is the case when the total number of jobs exceeds total number of machines. In this case, introduce required number of fictitious or dummy machines at ‘ 0’ cost or at the cost stated in the problem to get the balanced assignment problem. Then use the assignment technique to obtain the optimal assignment. The jobs which are assigned fictitious or dummy machines will be left over.

Illustration Machines exceeds Jobs

Problem J 1 J 2 J 3 J 4 M 1 2 4 3 5 M 2 3 8 9 12 In. M this given problem, there 3 4 12 are only four 11 jobs while 10 six machines. In an ideal condition there should be equal no of M 4 3 18 15 12 jobs so we need to make them equal. For this purpose we will introduce two 2 fictitious jobs M 5 22 at zero cost. 20 18 M 6 3 25 15 20 Requirement: Which job is to assign which machine to get the minimum cost
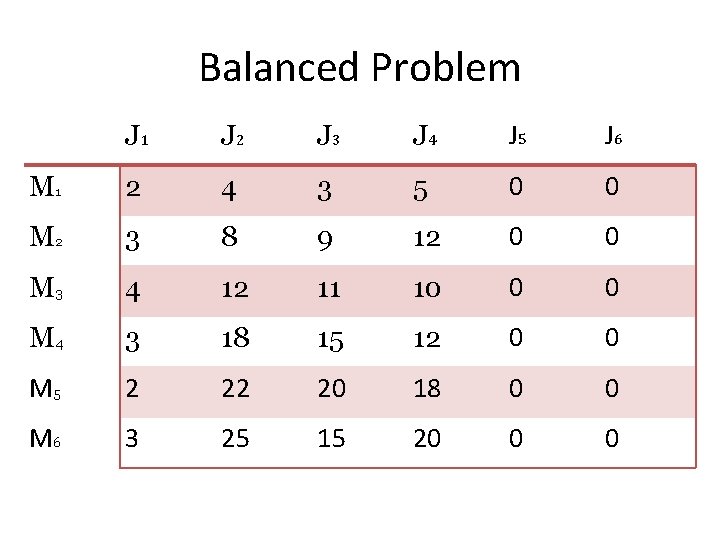
Balanced Problem J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 0 0 M 2 3 8 9 12 0 0 M 3 4 12 11 10 0 0 M 4 3 18 15 12 0 0 M 5 2 22 20 18 0 0 M 6 3 25 15 20 0 0
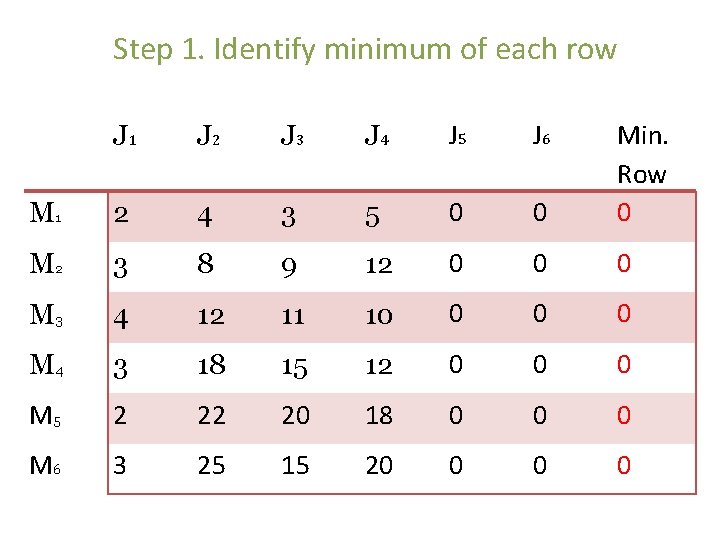
Step 1. Identify minimum of each row J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 0 0 Min. Row 0 M 2 3 8 9 12 0 0 0 M 3 4 12 11 10 0 M 4 3 18 15 12 0 0 0 M 5 2 22 20 18 0 0 0 M 6 3 25 15 20 0
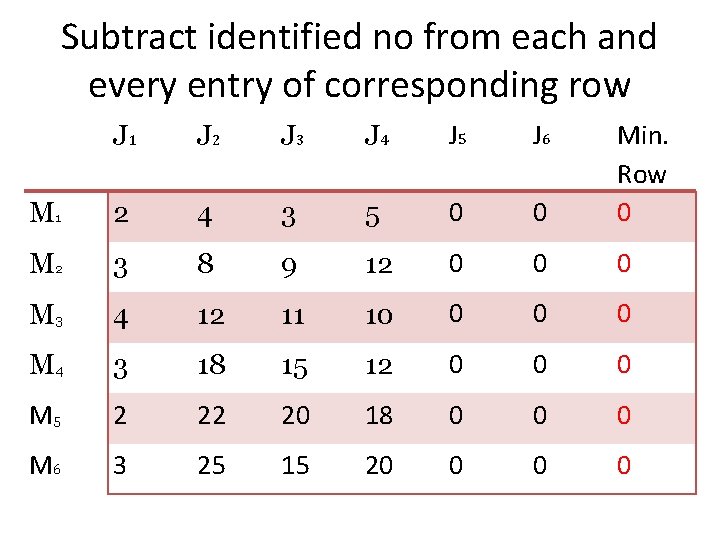
Subtract identified no from each and every entry of corresponding row J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 0 0 Min. Row 0 M 2 3 8 9 12 0 0 0 M 3 4 12 11 10 0 M 4 3 18 15 12 0 0 0 M 5 2 22 20 18 0 0 0 M 6 3 25 15 20 0
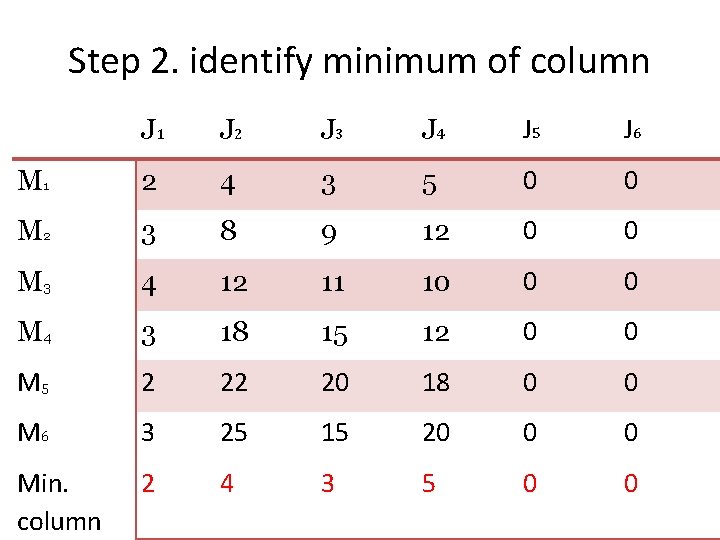
Step 2. identify minimum of column J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 0 0 M 2 3 8 9 12 0 0 M 3 4 12 11 10 0 0 M 4 3 18 15 12 0 0 M 5 2 22 20 18 0 0 M 6 3 25 15 20 0 0 Min. column 2 4 3 5 0 0
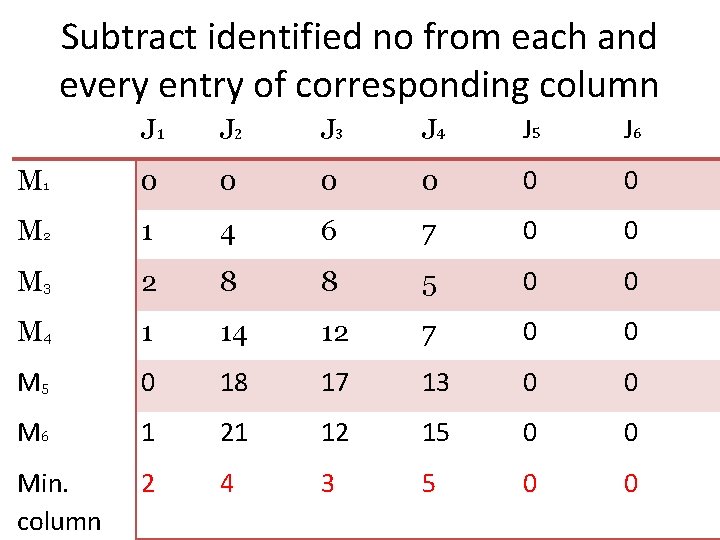
Subtract identified no from each and every entry of corresponding column J 1 J 2 J 3 J 4 J 5 J 6 M 1 0 0 0 M 2 1 4 6 7 0 0 M 3 2 8 8 5 0 0 M 4 1 14 12 7 0 0 M 5 0 18 17 13 0 0 M 6 1 21 12 15 0 0 Min. column 2 4 3 5 0 0
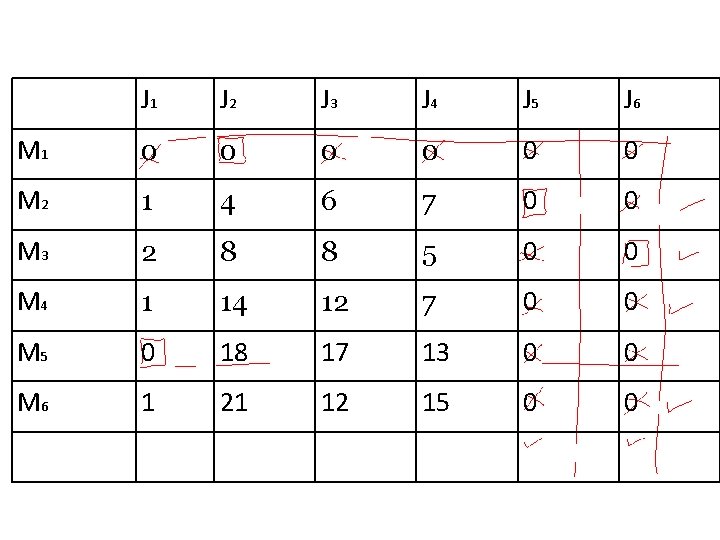
J 1 J 2 J 3 J 4 J 5 J 6 M 1 0 0 0 M 2 1 4 6 7 0 0 M 3 2 8 8 5 0 0 M 4 1 14 12 7 0 0 M 5 0 18 17 13 0 0 M 6 1 21 12 15 0 0
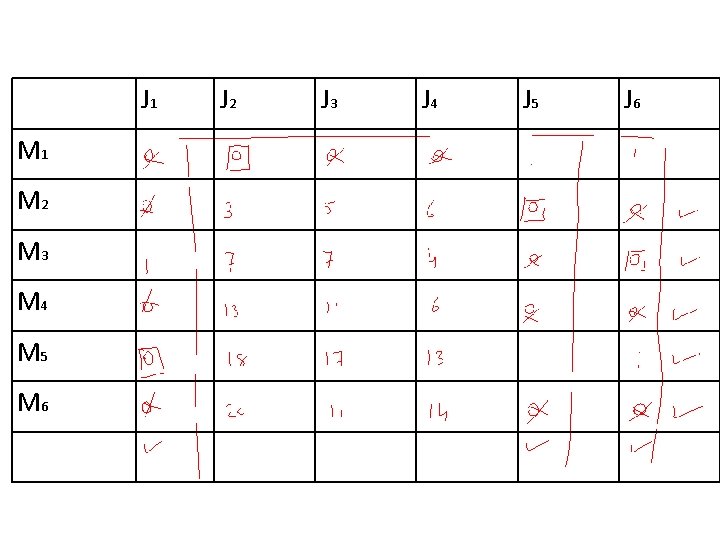
J 1 M 2 M 3 M 4 M 5 M 6 J 2 J 3 J 4 J 5 J 6
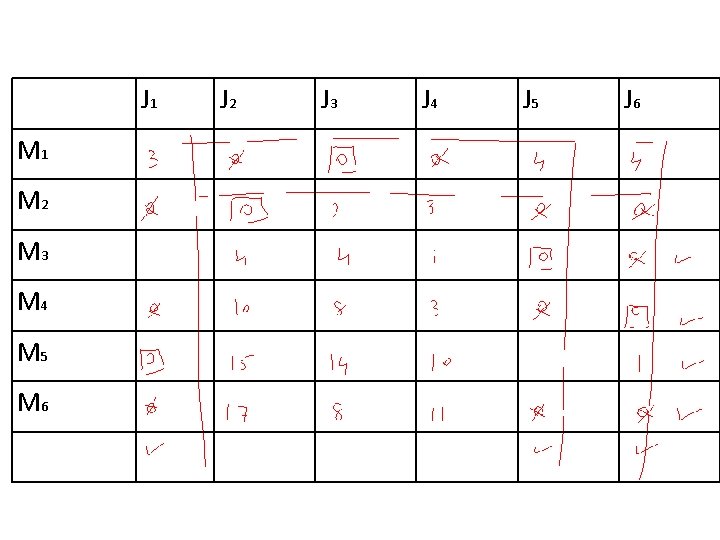
J 1 M 2 M 3 M 4 M 5 M 6 J 2 J 3 J 4 J 5 J 6
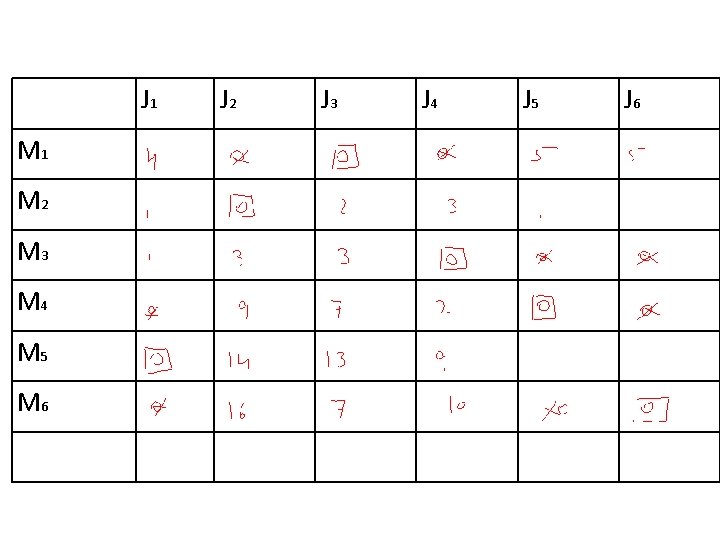
J 1 M 2 M 3 M 4 M 5 M 6 J 2 J 3 J 4 J 5 J 6
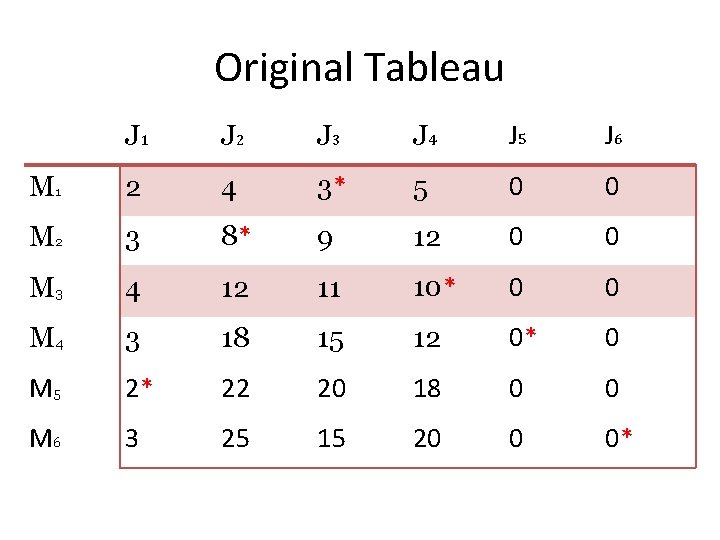
Original Tableau J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3* 5 0 0 M 2 3 8* 9 12 0 0 M 3 4 12 11 10* 0 0 M 4 3 18 15 12 0* 0 M 5 2* 22 20 18 0 0 M 6 3 25 15 20 0 0*

Optimal Distribution • M 1 ------- • M 2 ------- • M 3 ------- • M 4 ------- • M 5 ------- • M 6 ------- TOTAL J 3=3 J 2=8 J 4=10 J 5=0 J 1=2 J 6=0 =23

Illustration Jobs exceeds Machines

Problem J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 2 3 M 2 3 8 9 12 15 12 M 3 4 12 11 10 18 16 20 15 M 4 3 18 15 12 In this given problem, there are only four machines but six jobs. In an ideal condition there should be equal no of jobs Requirement: so we need to make them equal. For this purpose we will Which job is to assign which machine to get the introduce two fictitious Machines at zero cost. minimum cost
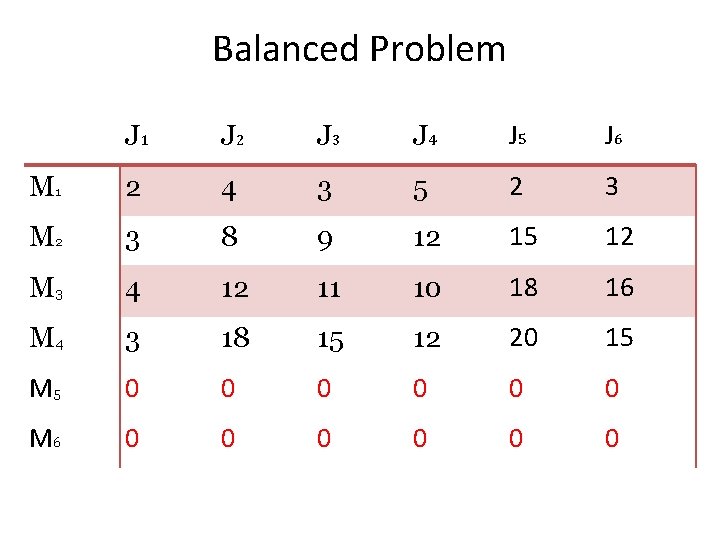
Balanced Problem J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 2 3 M 2 3 8 9 12 15 12 M 3 4 12 11 10 18 16 M 4 3 18 15 12 20 15 M 5 0 0 0 M 6 0 0 0
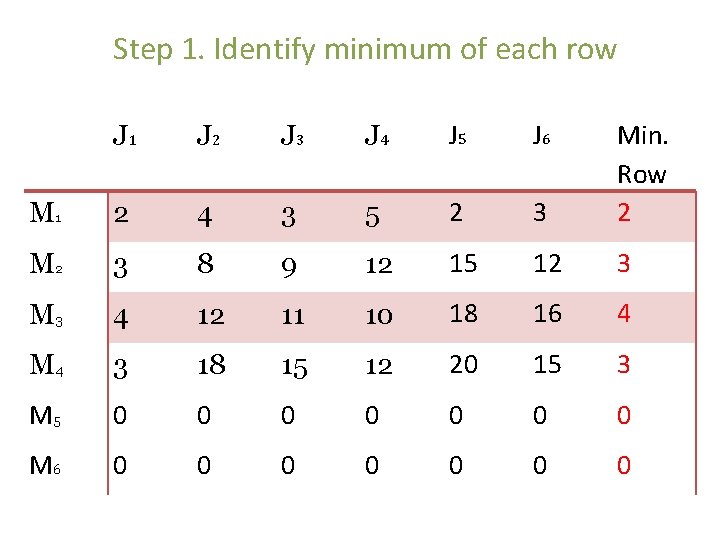
Step 1. Identify minimum of each row J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 2 3 Min. Row 2 M 2 3 8 9 12 15 12 3 M 3 4 12 11 10 18 16 4 M 4 3 18 15 12 20 15 3 M 5 0 0 0 0 M 6 0 0 0 0
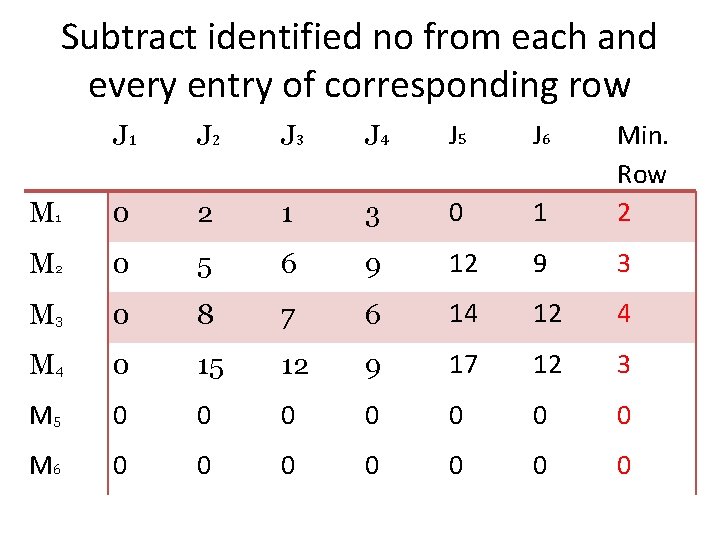
Subtract identified no from each and every entry of corresponding row J 1 J 2 J 3 J 4 J 5 J 6 M 1 0 2 1 3 0 1 Min. Row 2 M 2 0 5 6 9 12 9 3 M 3 0 8 7 6 14 12 4 M 4 0 15 12 9 17 12 3 M 5 0 0 0 0 M 6 0 0 0 0
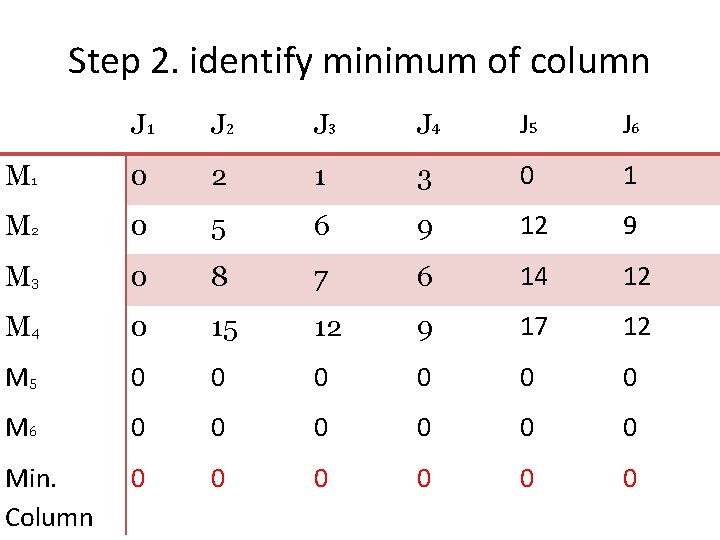
Step 2. identify minimum of column J 1 J 2 J 3 J 4 J 5 J 6 M 1 0 2 1 3 0 1 M 2 0 5 6 9 12 9 M 3 0 8 7 6 14 12 M 4 0 15 12 9 17 12 M 5 0 0 0 M 6 0 0 0 Min. Column 0 0 0
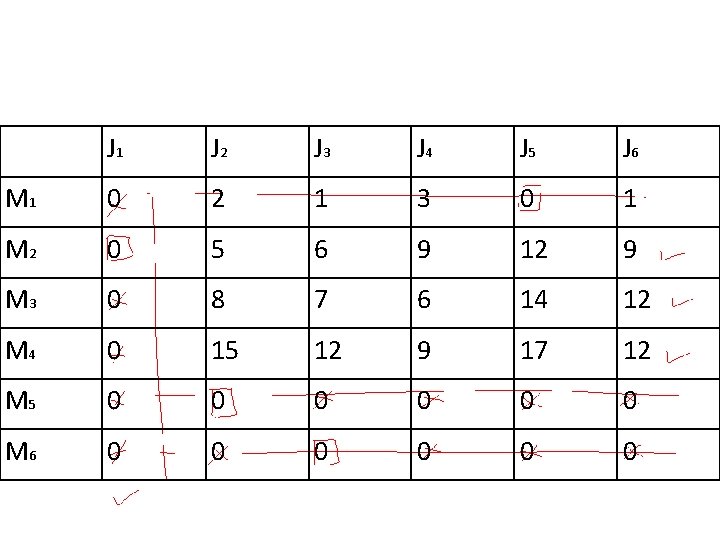
J 1 J 2 J 3 J 4 J 5 J 6 M 1 0 2 1 3 0 1 M 2 0 5 6 9 12 9 M 3 0 8 7 6 14 12 M 4 0 15 12 9 17 12 M 5 0 0 0 M 6 0 0 0
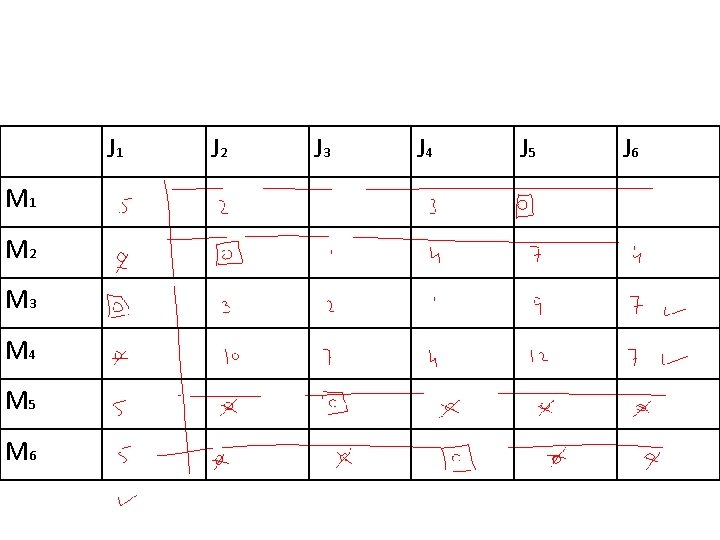
J 1 M 2 M 3 M 4 M 5 M 6 J 2 J 3 J 4 J 5 J 6
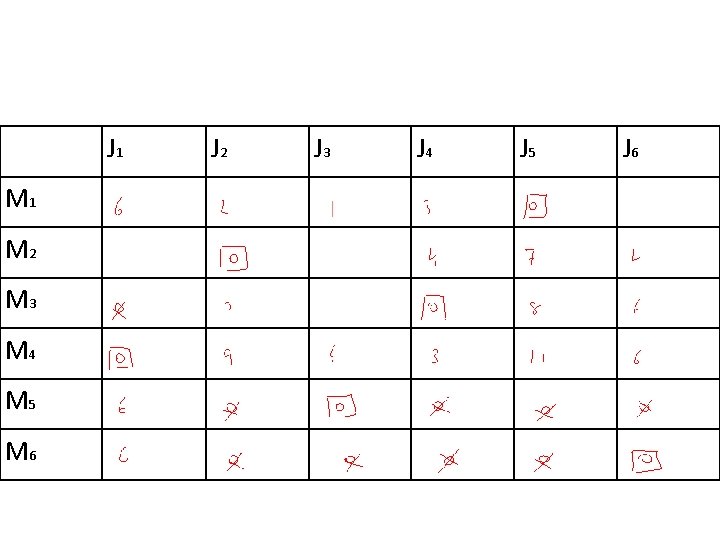
J 1 M 2 M 3 M 4 M 5 M 6 J 2 J 3 J 4 J 5 J 6
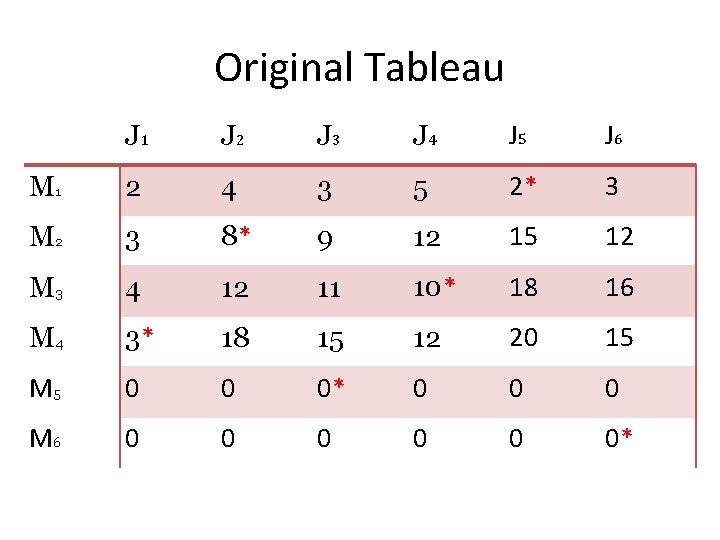
Original Tableau J 1 J 2 J 3 J 4 J 5 J 6 M 1 2 4 3 5 2* 3 M 2 3 8* 9 12 15 12 M 3 4 12 11 10* 18 16 M 4 3* 18 15 12 20 15 M 5 0 0 0* 0 0 0 M 6 0 0 0*

Optimal Distribution • M 1 ------- • M 2 ------- • M 3 ------- • M 4 ------- • M 5 ------- • M 6 ------- TOTAL J 5=2 J 2=8 J 4=10 J 1=3 J 3=0 J 6=0 =23

Thank You
- Slides: 29