Un esempio le liste ordinate di interi 1

Un esempio: le liste ordinate di interi 1

Liste ordinate 4 Ordered. Int. List 4 lista ordinata di interi – modificabile 2

Specifica di Ordered. Int. List 1 public class Ordered. Int. List { // OVERVIEW: una Ordered. Int. List è una lista // modificabile di interi ordinata // tipico elemento: [x 1, . . . , xn], xi<xj se i<j // costruttore public Ordered. Int. List () // EFFECTS: inizializza this alla lista vuota // metodi public void add. El (int el) throws Duplicate. Exception // MODIFIES: this // EFFECTS: aggiunge el a this, se el non occorre in // this, altrimenti solleva Duplicate. Exception public void rem. El (int el) throws Not. Found. Exception // MODIFIES: this // EFFECTS: toglie el da this, se el occorre in // this, altrimenti solleva Not. Found. Exception 3

Specifica di Ordered. Int. List 2 public boolean is. In (int el) // EFFECTS: se el appartiene a this ritorna // true, altrimenti false public boolean is. Empty () // EFFECTS: se this è vuoto ritorna true, altrimenti // false public int least () throws Empty. Exception // EFFECTS: se this è vuoto solleva Empty. Exception // altrimenti ritorna l’elemento minimo in this public boolean rep. Ok () public String to. String () // metodi test standard } 4

Specifica di Ordered. Int. List 3 public class Ordered. Int. List { public Ordered. Int. List () public void add. El (int el) throws Duplicate. Exception public void rem. El (int el) throws Not. Found. Exception public boolean is. In (int el) public boolean is. Empty () public int least () throws Empty. Exception public boolean rep. Ok () public String to. String ()} 4 Duplicate. Exception e Not. Found. Exception checked 5

Come implementarla? 4 Potremmo usare una struttura dati lineare: lista concatenata 4 lista concatenata: definizione ricorsiva 4 o e’ vuota 4 o e’ formata da un nodo, che contiene un valore (di tipo int) ed un puntatore al resto della lista 4 bisognerebbe mantenere i nodi ordinati in base al valore associato in ordine crescente (tipo esercizio di LIP) 6

Usiamo invece un albero binario 4 albero binario: struttura ricorsiva tipo lista 4 o e’ vuoto 4 o contiene un nodo (detto radice) a cui e’ associato un valore (in questo caso di tipo int) ed un puntatore a due alberi, detti sottoalbero sinistro e destro rispettivamente 4 Nota: si chiama binario esattamente perche’ ogni nodo ha due figli (si puo’ generalizzare) 7

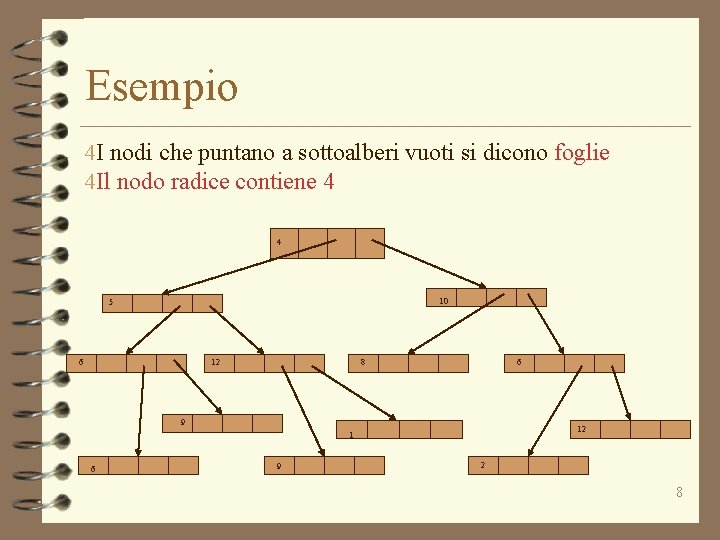
Esempio 4 I nodi che puntano a sottoalberi vuoti si dicono foglie 4 Il nodo radice contiene 4 4 10 5 6 12 8 6 6 12 1 6 6 2 8

Commenti 4 Rispetto ai tipi di dato lineari, lista doppia – si può percorrere da ogni elemento in avanti o all’indietro 4 Mediamente piu’ efficiente la ricerca se i valori sono inseriti in modo opportuno 4 Complessita’ degli algoritmi di inserimento, ricerca, eliminazione etc… (LSD, Algoritimica) 9

Ordinamento 4 Per mantenere l’ordinamento richiediamo che, per ogni nodo a cui e’ associato n 4 4 tutti i valori contenuti nel sottoalbero sinistro abbiano valore strettamente minore di n, tutti i valori contenuti nel sottoalbero destro abbiano valore strettamente maggiore di n. 10

Vantaggio 4 Se leggiamo i valori effettuando la visita dell’albero in ordine simmetrico otteniamo I valori ordinati in modo crescente 4 visita simmetrica: in modo ricorsivo, visitiamo prima il sottoalbero sinistro, poi la radice, poi il sottoalbero destro 4 Un esempio 11

Come lo implementiamo? public class Ordered. Int. List { // OVERVIEW: una Ordered. Int. List è una lista // modificabile di interi ordinata // tipico elemento: [x 1, . . . , xn], xi<xj se i<j private boolean vuota; private Ordered. Int. List prima, dopo; private int val; 4 la rep contiene – una variabile boolean che ci dice se la lista è vuota – la variabile intera che contiene l’eventuale valore dell’elemento – due (puntatori a) Ordered. Int. Lists che contengono la lista di quelli minori e quelli maggiori, rispettivamente 4 implementazione ricorsiva 12

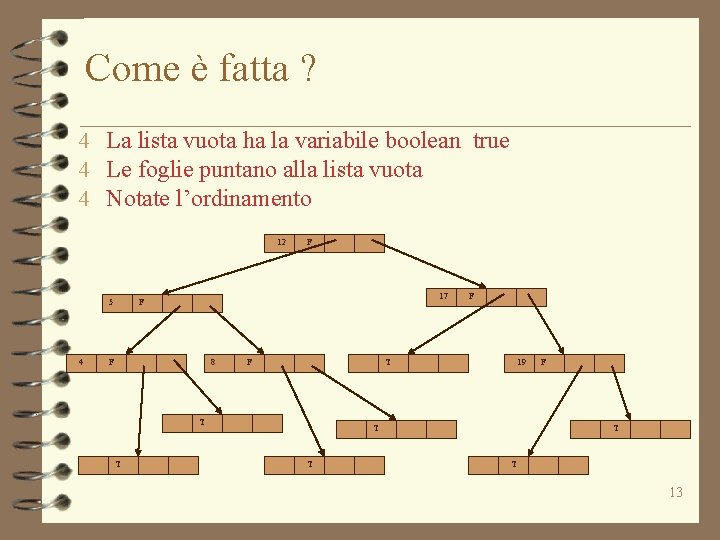
Come è fatta ? 4 La lista vuota ha la variabile boolean true 4 Le foglie puntano alla lista vuota 4 Notate l’ordinamento 12 5 4 F 17 F F 8 F T T T F 19 T T F T T 13

Commenti 4 L’invariante di rappresentazione e la funzione di astrazione descrivono le caratteristiche dell’implementazione che abbiamo in mente 4 Dipendono dalla rappresentazione e devono essere inserite commenti alla rappresentazione 4 Sono fondamentali per ragionare sulla correttezza dell’implementazione o per capire l’implementazione (se per esempio qualcuno la dovesse modificare) 14

Invariante private boolean vuota; private Ordered. Int. List prima, dopo; private int val; I(c) = c. vuota oppure (c. prima != null e c. dopo != null e I(c. prima) e I(c. dopo) e (!c. prima. is. Empty() -> c. prima. max() < c. val) e (!c. dopo. is. Empty() -> c. dopo. least() > c. val) ) 4 l’invariante esprime le proprieta’ che devono soddisfare gli oggetti concreti, ovvero le loro variabili d’istanza 4 In questo caso il ruolo di vuota e la relazione tra i valori contenuti nella radice e nei sottoalberi (necessarie per garantire l’ordinamento richiesto) 15

Funzione di astrazione private boolean vuota; private Ordered. Int. List prima, dopo; private int val; a(c) = se c. vuota allora [], altrimenti a(c) = a(c. prima) + [c. val] + a(c. dopo) 4 Mappa gli oggetti concreti, implementati con un albero binario, nella corrispondente lista ordinata in modo crescente, tipo [x 1, . . . , xn], xi<xj se i<j 4 La funzione di astrazione ricorsiva realizza la lettura dei valori in modo simmetrico (dato che la lista deve essere ordinata) 16

Esempio 4 Oggetto concreto x quello della figura 4 Oggetto astratto corrispondente e’ la seguente lista 4 a(x)= [4, 5, 12, 17, 19] 17

Nota 4 Oggetto concreto, implementato tramite un albero binario, non e’e non deve essere visibile a chi usa Ordered. Int. List 4 Oggetto astratto (a(this)) e’ visibile tramite il metodo to. String () che implementa la funzione di astrazione 4 Fondamentale se vogliamo conoscere lo stato dell’oggetto su cui stiamo lavorando, pur non avendo accesso diretto alla rappresentazione 4 Permette di fare delle verifiche sul comportamento dei metodi (creo un oggetto, inserisco dei valori, vedo se il risultato e’ quello atteso) 18

Domanda 4 4 4 Se abbiamo due implementazioni diverse (una fatta con l’albero binario e l’altra con una lista concatenata) Diverse invarianti e f. di astrazione Ma gli oggetti astratti devono essere dello stesso tipo, quello descritto nella OVERVIEW [x 1, . . . , xn], xi<xj se i<j 4 4 Da fuori vediamo solo gli oggetti astratti perche’ non vediamo differenze tra le due implementazioni (a parte chiaramente che possono differire in efficienza) Principio di base del tipo di dato astratto: la specifica e’ l’interfaccia con l’esterno e maschera l’implementazione 19

Esercizio 4 Fate l’implementazione con lista concatenata (tipo LIP) 4 Formalizzate la funzione di astrazione e l’invariante 4 Verificate che l’invariante valga 4 Verificate la correttezza dei metodi 4 Dal punto di vista di chi usa il tipo di dato non deve vedersi differenza 20

Esempio a(c) = a(c. prima) + [5] + a(c. dopo) = ([]+ [4]+[]) + [5] + ([]+ [8]+[])= [4, 5, 8] 4 Funzione di astrazione per il sottoalbero con radice 5 4 Se l’oggetto concreto non soddisfa l’invariante (che impone l’ordinamento) pero’ non e’ detto che troviamo I valori ordinati nel modo richiesto 4 Facciamo vedere che l’invariante impone dei vincoli sufficienti a garantire le proprieta’ dei dati richieste nella specifica 21

Invariante e Dati Astratti 4 Facciamo vedere per induzione sulla lunghezza della lista che Se I(c) allora a(c) =[x 1, . . . , xn], xi<xj se i<j 4 Caso Base: vale c. vuota. 4 Quindi a(c) = []. La lista vuota [] e’ ordinata. 22

Invariante 4 Caso Induttivo: non vale c. vuota, ma (c. prima != null e c. dopo != null e I(c. prima) e I(c. dopo) e (!c. prima. is. Empty() -> c. prima. max() < c. val) e (!c. dopo. is. Empty() -> c. dopo. least() > c. val) ) 4 Abbiamo a(c) = a(c. prima) + [c. val] + a(c. dopo)= [y 1, . . . , yn]+ [c. val] + [z 1, . . . , zk] 4 Dato che c. prima che c. dopo sono piu’ piccole di c, e che soddisfano l’invariante, allora per ipotesi induttiva [y 1, . . . , yn] e [z 1, . . . , zk] sono ordinate in modo crescente 4 Le altre proprieta’ dell’invariante garantiscono che sia anche tutta ordinata 23

Invariante 4 L’invariante cattura le proprieta’ richieste nella specifica dei dati, in particolare l’ordinamento degli interi crescente (l’abbiamo fatto vedere) 4 Rimangono da implemenatre i metodi in modo che preservino l’invariante 4 Discutiamo anche la loro correttezza rispetto alla specifica, assumendo che l’invariante valga, e utilizzando la funzione di astrazione per collegare la specifica che parla di oggetti astratti e l’implementazione che si riferisce agli oggetti concreti 24

Implementazione public class Ordered. Int. List { // OVERVIEW: una Ordered. Int. List è una lista // modificabile di interi ordinata // tipico elemento: [x 1, . . . , xn], xi<xj se i<j private boolean vuota; private Ordered. Int. List prima, dopo; private int val; // costruttore public Ordered. Int. List () // EFFECTS: inizializza this alla lista vuota { vuota = true; } 4 il costruttore inizializza solo la variabile vuota 4 l’oggetto prodotto soddisfa l’invariante (c. vuota = true) 4 verifica la propria specifica (a(c) = []) 25

Inserire e rimuovere 4 Difficili perche’ bisogna preservare l’ordinamento 4 Le proprieta’ dell’ordinamento sono espresse dall’invariante (ci aiuta a non fare errori in una situazione un po’ complessa) 4 Vediamo un esempio 26

Inserire un elemento public void add. El (int el) throws Duplicate. Exception // MODIFIES: this // EFFECTS: aggiunge el a this, se el non occorre in // this, altrimenti solleva Duplicate. Exception {if (vuota) { prima = new Ordered. Int. List(); dopo = new Ordered. Int. List(); val = el; vuota = false; return; } if (el == val) throw new Duplicate. Exception(“Ordered. Int. List. add. El”); if (el < val) prima. add. El(el); else dopo. add. El(el); } 4 Ricorsiva, inserisce rispettando l’ordinamento 4 Propaga automaticamente l’eventuale eccezione sollevata dalle chiamate ricorsive 27

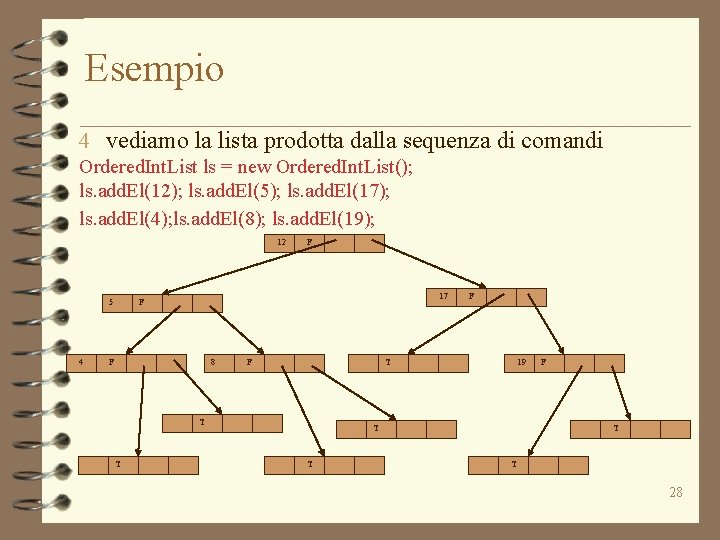
Esempio 4 vediamo la lista prodotta dalla sequenza di comandi Ordered. Int. List ls = new Ordered. Int. List(); ls. add. El(12); ls. add. El(5); ls. add. El(17); ls. add. El(4); ls. add. El(8); ls. add. El(19); 12 5 4 F 17 F F 8 F T T T F 19 T T F T T 28

Invariante: per casi I(c) = c. vuota oppure (c. prima != null e c. dopo != null e I(c. prima) e I(c. dopo) e (!c. prima. is. Empty() -> c. prima. max() < c. val) e (!c. dopo. is. Empty() -> c. dopo. least() >= c. val) ) public void add. El (int el) throws Duplicate. Exception {if (vuota) { prima = new Ordered. Int. List(); dopo = new Ordered. Int. List(); val = el; vuota = false; return; } . . . prima != null e dopo != null (calcolati dal costruttore) I(prima) e I(dopo) (calcolati dal costruttore) le implicazioni sono vere perché la premessa è falsa 29

Invariante: this non vuoto I(c) = c. vuota oppure (c. prima != null e c. dopo != null e I(c. prima) e I(c. dopo) e (!c. prima. is. Empty() -> c. prima. max() < c. val) e (!c. dopo. is. Empty() -> c. dopo. least() >= c. val) ) public void add. El (int el) throws Duplicate. Exception. . . if (el < val) prima. add. El(el); else dopo. add. El(el); } 4 prima != null e dopo != null (this non e’ vuoto) I(prima) e I(dopo) (calcolati da una chiamata ricorsiva su una lista piu’ piccola) 4 ramo then: il nuovo massimo di prima è (induttivamente) minore di val 4 ramo else: il nuovo minimo di dopo è (induttivamente) maggiore di val 30

Specifica a(c) = se c. vuota allora [], altrimenti a(c. prima) + [c. val] + a(c. dopo) public void add. El (int el) throws Duplicate. Exception // MODIFIES: this // EFFECTS: aggiunge el a this, se el non occorre in // this, altrimenti solleva Duplicate. Exception {if (vuota) { prima = new Ordered. Int. List(); dopo = new Ordered. Int. List(); val = el; vuota = false; return; }. . . 4 a(cpre) = [] 4 a(c. prima) = [] e a(c. dopo) = [] e [c. val] = [el] 4 a(c) = [el] (ha inserito l’elemento) 31

Specifica public class Ordered. Int. List { private boolean vuota; private Ordered. Int. List prima, dopo; private int val; // a(c) = se c. vuota allora [], altrimenti // a(c. prima) + [c. val] + a(c. dopo) public void add. El (int el) throws Duplicate. Exception // MODIFIES: this // EFFECTS: aggiunge el a this, se el non occorre in // this, altrimenti solleva Duplicate. Exception. . . if (el == val) throw new Duplicate. Exception(“Ordered. Int. List. add. El”); 4 se ci sono elementi duplicati solleva l’eccezione, eventualmente propagando eccezioni sollevate dalle chiamate ricorsive (vedi dopo) 32

Specifica // a(c) = se c. vuota allora [], altrimenti // a(c. prima) + [c. val] + a(c. dopo) public void add. El (int el) throws Duplicate. Exception // MODIFIES: this // EFFECTS: aggiunge el a this, se el non occorre in // this, altrimenti solleva Duplicate. Exception. . . if (el < val) prima. add. El(el); else dopo. add. El(el); } 4 4 4 a(cpre) = a(c. primapre) + [c. val] + a(c. dopopre) se el < val la chiamata ricorsiva solleva l’eccezione oppure produce a(c. prima) = aggiunge el a primapre a(c. dopo) = a(c. dopopre) a(c) = aggiunge el a cpre Analogo nel caso simmetrico 33

Rimuovere un elemento 4 Difficile, bisogna mantenere l’ordinamento 4 Supponiamo di dovere rimuovere 12 (e’ la radice) 4 Non possiamo semplicemente spostare nella radice uno dei nodi figli (ex. 5) 34

Idea 4 si prende il valore minimo del dopo (se c’e’) e si mette al posto della radice (e si rimuove dal dopo) 4 e’ di sicuro piu’ grande di tutti i valori di prima e piu’ piccolo di quelli di dopo 4 se dopo e’ vuoto allora si ricopia nel nodo radice il sottoalbero prima 4 in questo modo viene preservato l’ordinamento imposto dall’ordinamento 35

Implementazione di Ordered. Int. List 5 public void rem. El (int el) throws Not. Found. Exception // MODIFIES: this // EFFECTS: toglie el da this, se el occorre in // this, altrimenti solleva Not. Found. Exception {if (vuota) throw new Not. Found. Exception(“Ordered. Int. List. rem. El”); if (el == val) try { val = dopo. least(); dopo. rem. El(val); } catch (Empty. Exception e) { vuota = prima. vuota; val = prima. val; dopo = prima. dopo; prima = prima; return; } else if (el < val) prima. rem. El(el); else dopo. rem. El(el); } 36

Implementazione di Ordered. Int. List 6 public boolean is. In (int el) // EFFECTS: se el appartiene a this ritorna // true, altrimenti false {if (vuota) return false; if (el == val) return true; if (el < val) return prima. is. In(el); else return dopo. is. In(el); } public boolean is. Empty () // EFFECTS: se this è vuoto ritorna true, altrimenti false {return vuota; } Si ricerca in base all’ordinamento (efficiente, non si visita tutto) 37

Implementazione di Ordered. Int. List 6. 1 public class Ordered. Int. List { private boolean vuota; private Ordered. Int. List prima, dopo; private int val; // a(c) = se c. vuota allora [], altrimenti // a(c. prima) + [c. val] + a(c. dopo) public boolean is. In (int el) // EFFECTS: se el appartiene a this ritorna // true, altrimenti false {if (vuota) return false; if (el == val) return true; if (el < val) return prima. is. In(el); else return dopo. is. In(el); } public boolean is. Empty () // EFFECTS: se this è vuoto ritorna true, altrimenti false {return vuota; } 4 dimostrazioni di correttezza ovvie, visto che l’invariante che garantisce l’ordinamento 38

Implementazione di Ordered. Int. List 7. 1 public class Ordered. Int. List { private boolean vuota; private Ordered. Int. List prima, dopo; private int val; public int least () throws Empty. Exception // EFFECTS: se this è vuoto solleva Empty. Exception // altrimenti ritorna l’elemento minimo in this {if (vuota) throw new Empty. Exception(“Ordered. Int. List. least”); try { return prima. least(); } catch (Empty. Exception e) {return val; } } 4 4 dimostrazione di correttezza ovvia usando l’invariante, che garantisce l’ordinamento Ritorna proprio il primo elemento di a(this) 39

Implementazione di Ordered. Int. List 7. 1 public class Ordered. Int. List { private boolean vuota; private Ordered. Int. List prima, dopo; private int val; public String to. String(){ // EFFECTS: standard {if (vuota) return “”; return prima. to. String() + val + dopo. to. String(); } } 4 dimostrazione di correttezza ovvia usando l’invariante, che garantisce l’ordinamento 4 Implementa a(this) visita in ordine simmetrico 40