UMass Lowell Computer Science 91 503 Analysis of

UMass Lowell Computer Science 91. 503 Analysis of Algorithms Prof. Karen Daniels Spring, 2005 Lecture 6 Wednesday, 3/8/05 NP-Completeness

Overview ä NP-Completeness, Part 1 ä Graham videotape ä Review: Reduction to Establish Lower Bounds ä Basics ä NP-Completeness, Part 2 ä More basics ä How to Treat NP- Hard or Complete Problems

Resources -Recommended: ä Computers & Intractability by Garey & Johnson ä W. H. Freeman ä 1990 ä ISBN 0716710455. ä

Motivation

Why do we care? ? ä When faced with a problem in practice, need to know whether or not one can expect produce a “fast” algorithm (i. e. O(nk)) to solve it ä “Intractable” problems occur frequently in practice ä Surface differences between tractable and intractable problems are often hard to see ä e. g. MST solvable in polynomial time but Dominating Set intractable

Dominating Set source: Garey & Johnson

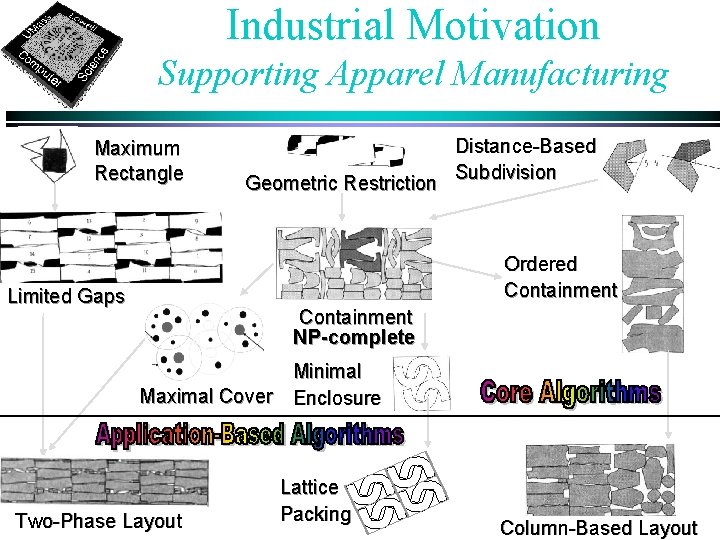
Industrial Motivation Supporting Apparel Manufacturing Maximum Rectangle Geometric Restriction Distance-Based Subdivision Ordered Containment Limited Gaps Containment NP-complete Minimal Maximal Cover Enclosure Two-Phase Layout Lattice Packing Column-Based Layout

Covering Research Example: Translational 2 D Covering [CCCG’ 01, CCCG’ 03 conference papers] ä Input: STATIC ä Covering polygons Q = {Q 1, Q 2 , . . . , Qm} ä Target polygons (or point-sets) P = {P 1, P 2 , . . . , Pn} ä Output: ä Translations g = {g 1, g 2 , . . . , g m} such that P 2 Translational 2 D Polygon Covering P 2 P 1 Q 3 Q 1 Q 2 P 1 Q 3 Sample P and Q NP-COMPLETE Q 2 Q 1 Translated Q Covers P

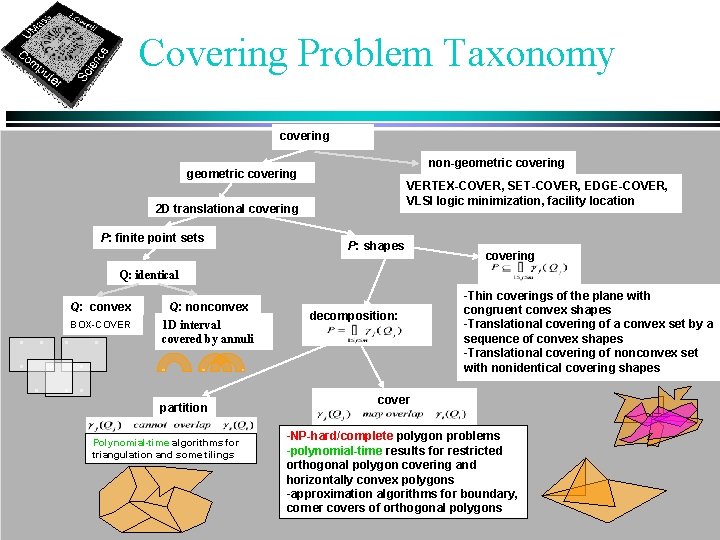
Covering Problem Taxonomy covering non-geometric covering VERTEX-COVER, SET-COVER, EDGE-COVER, VLSI logic minimization, facility location 2 D translational covering P: finite point sets P: shapes covering Q: identical Q: convex Q: nonconvex BOX-COVER 1 D interval covered by annuli . . . partition : Polynomial-time algorithms for triangulation and some tilings decomposition: . -Thin coverings of the plane with congruent convex shapes -Translational covering of a convex set by a sequence of convex shapes -Translational covering of nonconvex set with nonidentical covering shapes cover -NP-hard/complete polygon problems -polynomial-time results for restricted orthogonal polygon covering and horizontally convex polygons -approximation algorithms for boundary, corner covers of orthogonal polygons

Reduction to Establish Lower Bound Tightening a Lower Bound for Maximum-Area Axis-Parallel Rectangle Problem from W(n) to W(nlgn)

Approach ä Go around lower bound brick wall by: ä examining strong lower bounds for some similar problems ä transforming a similar problem to the rectangle problem [this process is similar to what we do when we prove problems NP-complete] worst-case bounds on problem 1 n n log 2 n n 2 n 5 2 n

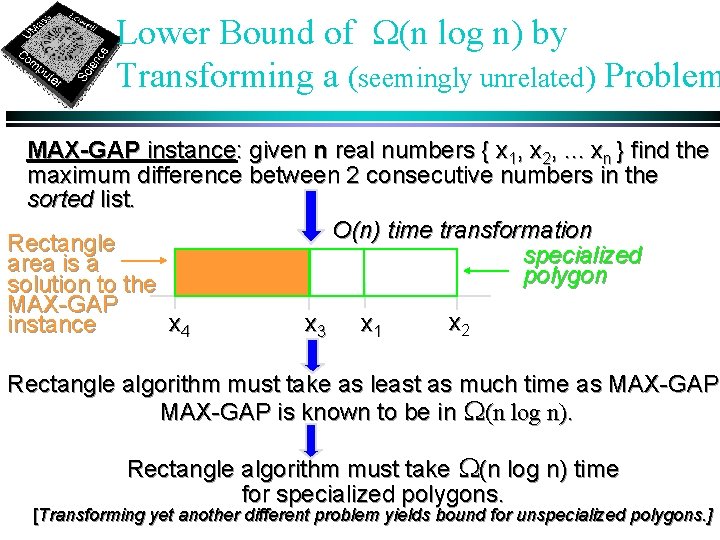
Lower Bound of W(n log n) by Transforming a (seemingly unrelated) Problem MAX-GAP instance: given n real numbers { x 1, x 2, . . . xn } find the maximum difference between 2 consecutive numbers in the sorted list. O(n) time transformation Rectangle specialized area is a polygon solution to the MAX-GAP x 2 x 4 x 3 x 1 instance Rectangle algorithm must take as least as much time as MAX-GAP is known to be in W(n log n). Rectangle algorithm must take W(n log n) time for specialized polygons. [Transforming yet another different problem yields bound for unspecialized polygons. ]

NP-Completeness Chapter 34

Basic Concepts Polynomial Time & Problem Formalization Polynomial-Time Verification NP-Completeness & Reducibility NP-Completeness Proofs Expanding List of Hard Problems via Reduction

Polynomial Time & Problem Formalization ä Formalize notions of abstract and concrete decision problems ä Encoding a problem ä Define class of polynomial-time solvable decision problems ä Define complexity class ä Express relationship between decision problems and algorithms that solve them using framework of formal language theory

Polynomial Time & Problem Formalization (continued) ä Solvable in Polynomial Time ä i. e. O(nk) for some positive constant k ä Tractable: k is typically small (e. g. 1, 2, 3) ä Typically holds across computation models ä Closure properties (chaining/composition) ä Abstract Problem: ä Binary relation on set of problem instances & solutions ä Decision Problem: yes/no answer ä impose bound on optimization problem to recast ä e. g. Dominating Set

Dominating Set source: Garey & Johnson

Polynomial Time & Problem Formalization (continued) ä ä ä Encoding of set S of abstract objects is mapping e from S to set of bi Concrete Problem: instance set is set of binary strings Concrete Problem is Polynomial-Time Solvable if there exists an alg Complexity Class P = set of polynomial-time solvable concrete de Given abstract decision problem Q that maps instance set I to {0, 1} If solution to abstract-problem instance ä then solution to concrete-problem instance is also Q(i)

Polynomial Time & Problem Formalization (continued) Goal: Extend definition of polynomial-time solvability from concrete to abstract using encodings as bridge ä is polynomial-time computable if there exists a polynomial-tim For set I of problem instances, encodings are polynomially related if there exist 2 po ä If 2 encodings e 1, e 2 of abstract problem are polynomially related, then polynomial-ti ä Lemma 34. 1: Let Q be an abstract decision problem on an instance set I and let e 1, e 2 be polynomially related encodings on I. Then,

Polynomial Time & Problem Formalization (continued) ä Formal Language Framework ä ä ä Alphabet S is finite set of symbols: Language L over S is any set of strings consisting of symbols f Set of instances for decision problem Q is View Q as language L over S = {0, 1} Express relation between decision problems and algorithms ä ä Algorithm A accepts string if, given input x, output A(x) is 1 Language accepted by A is set of strings A accepts

Polynomial Time & Problem Formalization (continued) ä Formal Language Framework (continued) ä ä ä Language L is decided by algorithm A if every binary string in L Language L is accepted in polynomial time by algorithm A if i Language L is decided in polynomial time by algorithm A if ex

Polynomial Time & Problem Formalization (continued) ä Formal Language Framework (continued) ä Complexity Class is a set of languages whose membership is determined by a complexity measure (i. e. running time) of algorithm that determines whether a given string belongs to a language. ä We already defined: Complexity Class P = set of polynomial-time solvable concrete decision problems Language Framework gives other definitions: ä P={ : there exists an algorithm A that decides L in polynomial time} = { L : L is accepted by a polynomial-time algorithm}

Polynomial-Time Verification ä Examine algorithms that “verify” membership in languages ä Define class of decision problems whose solutions can be verified in polynomial time

Polynomial-Time Verification (con ä Verification Algorithms ä algorithm A verifies language L if for any string ä also, for any string certificate y that A can use to p language verified by verification algorithm A is ä

Polynomial-Time Verification (con ä ä The Complexity Class NP ä languages that can be verified by a polynomial-time algorithm ä A verifies language L in polynomial time The Complexity Class co-NP ä set of languages L such that

Polynomial-Time Verification (con P P P 34. 3 source: 91. 503 textbook Cormen et al.

NP-Completeness & Reducibility ä Polynomial-Time Reducibility ä Define complexity class of NP-complete problems ä Relationships among complexity classes ä Circuit satisfiability as an NP-complete problem

NP-Completeness & Reducibility ä ä Q can be reduced to Q’ if any instance of Q can be “easily rephrased L 1 is polynomial-time reducible to L 2 : 34. 4 source: 91. 503 textbook Cormen et al.

NP-Completeness & Reducibility 34. 5 34. 3 source: 91. 503 textbook Cormen et al.

NP-Completeness & Reducibility (continued) Language and without this condition, language is only NP-hard popular theoretical computer science view is NP-complete if NP set of all NPcomplete languages Theorem: - If any NP-complete problem is polynomial-time solvable, then P=NP. - Equivalently, if any problem in NP is not polynomial-time solvable, then no NP-complete problem is polynomial-time solvable. source: 91. 503 textbook Cormen et al.

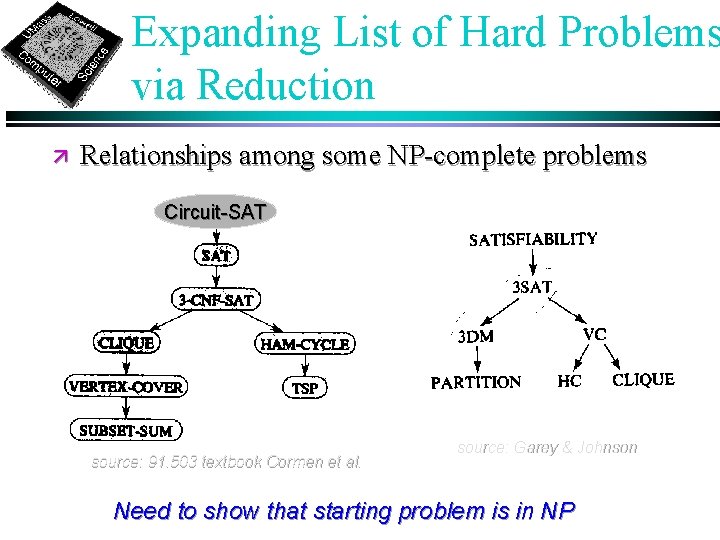
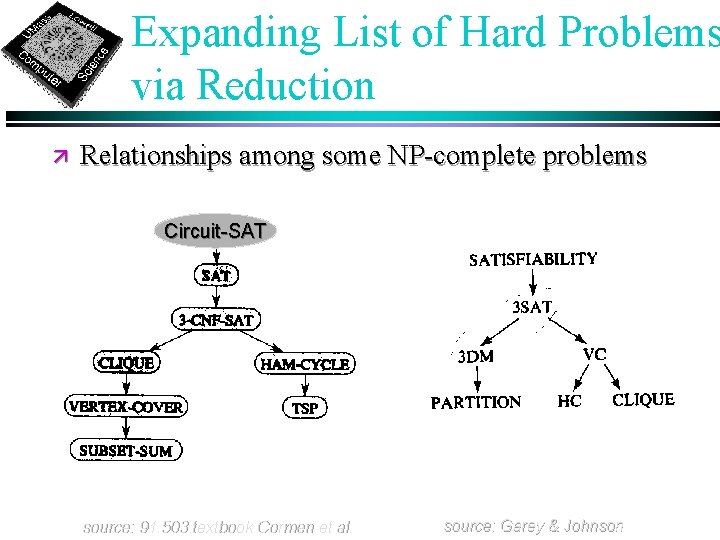
Expanding List of Hard Problems via Reduction ä Relationships among some NP-complete problems Circuit-SAT source: 91. 503 textbook Cormen et al. source: Garey & Johnson Need to show that starting problem is in NP

NP-Completeness & Reducibility (continued): Circuit Satisfiability circuit inputs ä Satisfying Assignment: truth assignment inducing output = 1 single circuit output Boolean Combinational Gate Types: AND, NOT, OR Language Def: CIRCUIT-SAT = {<C>: C is a satisfiable boolean combinational circuit. } ä GOAL: Show Circuit Satisfiability is NP-complete 34. 8 source: 91. 503 textbook Cormen et al.

NP-Completeness & Reducibility (continued) Circuit Satisfiability ä CIRCUIT-SAT is in NP: ä Construct 2 -input polynomial-time algorithm A that verifies CIRCUIT-SAT ä ä ä Algorithm A : ä ä ä Input 1: encoding of circuit C Input 2: certificate = assignment of boolean values to all wires of C For each logic gate A checks if certificate value for gate’s output wire correctly computes gate’s function based on input wire values If output of entire circuit is 1, algorithm outputs 1 Otherwise, algorithm outputs 0 For satisfiable circuit, there is a (polynomial-length) certificate that causes A to output 1 For unsatisfiable circuit, no certificate can cause A to output 1 Algorithm A runs in polynomial time source: 91. 503 textbook Cormen et al.

NP-Completeness & Reducibility (continued) ä Circuit Satisfiability CIRCUIT-SAT is NP-hard: ä ä L represents some language in NP Create polynomial-time algorithm F computing reduction function f that maps every binary string x to a circuit C=f(x) such that ä ä ä Must exist algorithm A verifying L in polynomial time. (A from NP) F uses A to compute f. Represent computation of A as sequence of configurations F constructs single circuit that computes all configurations produced by initial configuration source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Proving a Language NP-Complete ä Proving a Language NP-Hard ä all steps except (1) source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Reducing Boolean Circuit Satisfiability to Boolean Form ä Boolean Formula Satisfiability: Instance of language SAT is a ä ä n boolean variables: x 1, x 2, . . . , xn m boolean connectives: boolean function with 1 or 2 inputs and 1 outpu ä ä ä e. g. AND, OR, NOT, implication, iff parentheses truth, satisfying assignments notions apply source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Show: SAT is NP-Complete ä SAT is in NP via argument similar to circuit case ä Reduce Boolean Circuit Satisfiability to Boolean Formula Satisfiability ä Careful! Naive approach might have shared subformulas and cause formula size to grow exponentially! source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Show: SAT is NP-Complete (continued) ä Reduce Boolean Circuit Satisfiability to Boolean Formula Satisfiability (continued) ä Approach: For each wire xi in circuit C, formula f has variable xi. Express gate operation. 34. 10 source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Reducing Formula Satisfiability to 3 -CNFSatisfiability ä ä Boolean Formula Satisfiability: Instance of language SAT is a boolean formula f CNF = conjunctive normal form ä ä conjunction: AND of clauses clause: OR of literal(s) 3 -CNF: each clause has exactly 3 distinct literals Show: 3 -CNF is NP-Complete source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Show: 3 -CNF is NP-Complete (continued) ä 3 CNF is in NP via argument similar to circuit case ä Reduce Formula Satisfiability to 3 -CNF-Satisfiability ä 3 steps progressively transforming formula f closer to 3 CNF ä 1) Similar to reduction Binary “Parse. Tree” 34. 11 source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Show: 3 -CNF is NP-Complete (continued) ä 3 CNF is in NP via argument similar to circuit case ä Reduce Formula Satisfiability to 3 -CNF-Satisfiability ä 3 steps progressively transforming formula f closer to 3 CNF ä 2) Convert each clause fi’ into conjunctive normal form ä construct truth table for fi’ ä using entries for 0, build DNF formula for ä convert DNF into CNF formula fi” by applying De. Morgan’s laws ä each clause has at most 3 literals source: 91. 503 textbook Cormen et al.

NP-Completeness Proofs (continued) ä Show: 3 -CNF is NP-Complete (continued) ä 3 CNF is in NP via argument similar to circuit case ä Reduce Formula Satisfiability to 3 -CNF-Satisfiability ä 3 steps progressively transforming formula f closer to 3 CNF ä ä 3) Convert each clause fi” so it has exactly 3 distinct literals ä add “padding variables” ä create fi”’ Size of resulting formula is polynomial in length of original formula and reduction takes only polynomial time and 3 -CNF formula source: 91. 503 textbook Cormen et al.

Expanding List of Hard Problems via Reduction ä Relationships among some NP-complete problems Circuit-SAT source: 91. 503 textbook Cormen et al. source: Garey & Johnson

Vertex Cover A Vertex Cover of an undirected graph G=(V, E) is a subset B vertex cover of size 2 C D E F source: Garey & Johnson

Dominating Set source: Garey & Johnson

Clique of an undirected graph G=(V, E) is a complete subgraph of G. A B C clique of size 3 D E F source: Garey & Johnson

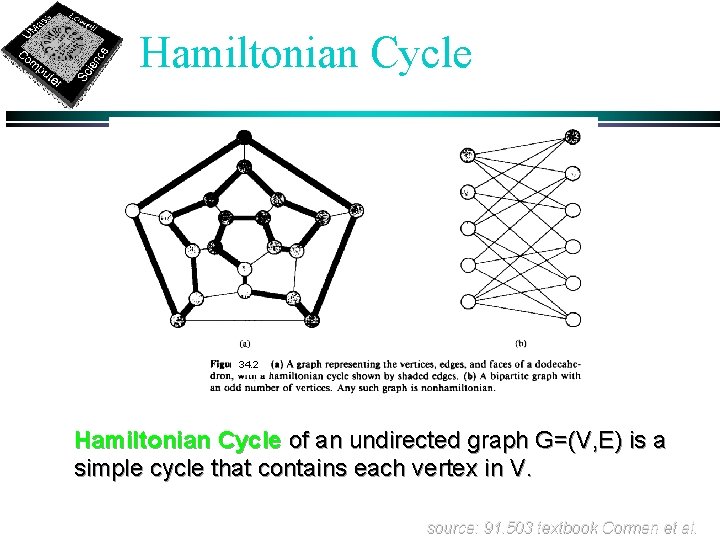
Hamiltonian Cycle 34. 2 Hamiltonian Cycle of an undirected graph G=(V, E) is a simple cycle that contains each vertex in V. source: 91. 503 textbook Cormen et al.

Reducing 3 -CNF-SAT to Clique source: 91. 503 textbook Cormen et al. Construct graph G such that f is satisfiable iff G has clique of size k x 1 x 3 x 1 x 2 34. 14 For each clause place triple of vertices v 1 r , v 2 r , v 3 r into V. Put edge for vir , vjs if corresponding literals consistent and r not= s.

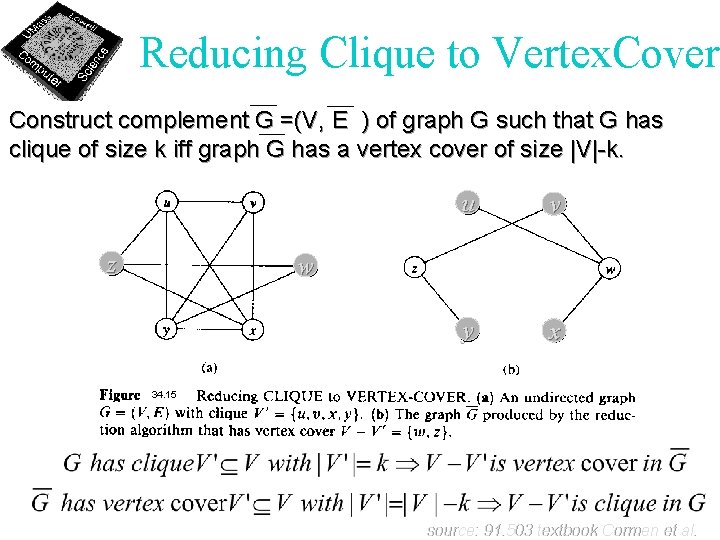
Reducing Clique to Vertex. Cover Construct complement G =(V, E ) of graph G such that G has clique of size k iff graph G has a vertex cover of size |V|-k. z u v y x w 34. 15 source: 91. 503 textbook Cormen et al.

How to Treat NP-Hard or Complete Problems

How to Treat NP-Complete Problems? ? ä Approximation Algorithms ä Heuristic Upper or Lower Bounds ä Greedy, Simulated Annealing, Genetic “Alg”, AI ä Mathematical Programming ä Linear Programming for part of problem ä Integer Programming ä Quadratic Programming. . . ä Search Space Exploration: ä Gradient Descent, Local Search, Pruning, Subdivision ä Randomization, Derandomization ä Leverage/Impose Problem Structure ä Leverage Similar Problems