Umans Complexity Theory Lectures Lecture 1 c Robust

Umans Complexity Theory Lectures Lecture 1 c: Robust Time & Space Classes

Complexity Classes • Back to complexity classes: – TIME(T(n)) = languages decidable by a multitape TM in at most T(n) steps, where n is the input length, and T : N → N – SPACE(S(n)) = languages decidable by a multi-tape TM that touches at most S(n) cells of its work tapes, where n is the input length, and S : N → N Note: P = k > 1 TIME(nk) 2

Proper Complexity Functions Let f : N → N be a resource bound (e. g. , time or space bound) • Definition: f is a proper complexity function if – f(n) ≥ f(n-1) for all n – f is constructable: there exists a TM M that outputs exactly f(n) symbols on input 1 n, and runs in time O(f(n) + n) and space O(f(n)). 3

Proper Complexity Functions • include all reasonable functions we will work with – log n, √n, n 2, 2 n, n!, … – if f and g are proper then f + g, f(g), fg, 2 g are all proper • can mostly ignore, but be aware it is a genuine concern: • Can prove: ∃ non-proper complexity function f such that TIME(T(n)) = TIME(2 T(n)). 4

Hierarchy Theorems • Does genuinely more space or time permit us to decide new languages? Theorem (Space Hierarchy Theorem): For every proper complexity function S(n) ≥ log n: SPACE(o(S(n))) ⊊ SPACE(S(n)). Theorem (Time Hierarchy Theorem): For every proper complexity function T(n) ≥ n: TIME(T(n)) ⊊ TIME(T(n)2) (for 1 tape TMs) TIME(T(n)) ⊊ TIME(T(n) log T(n)) (for multitape TMs) • Proofs: Diagonalization 5

Robust Time and Space Classes • What is meant by “robust” class? – no formal definition – reasonable changes to model of computation shouldn’t change class – should allow “modular composition” – calling subroutine in class (for classes closed under complement…) 6

Robust Time and Space Classes • Robust time and space classes: L = SPACE(log n) PSPACE = k SPACE(nk) P = k TIME(nk) k n EXP = k TIME(2 ) 7

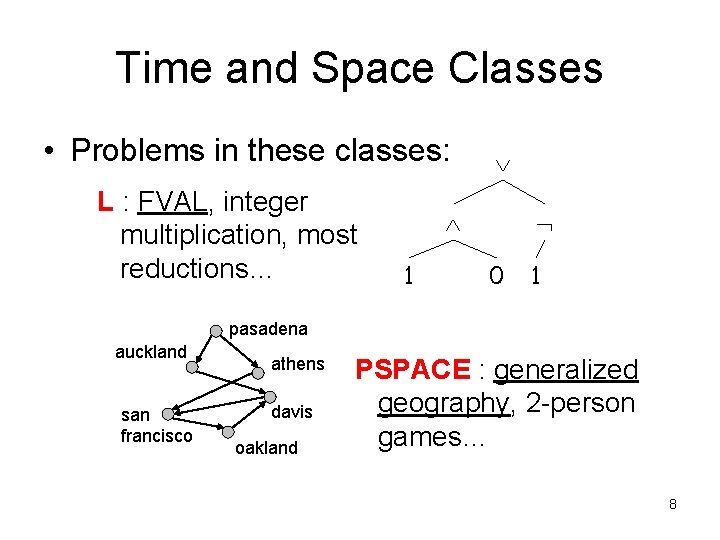
Time and Space Classes • Problems in these classes: L : FVAL, integer multiplication, most reductions… 1 0 1 pasadena auckland san francisco athens davis oakland PSPACE : generalized geography, 2 -person games… 8

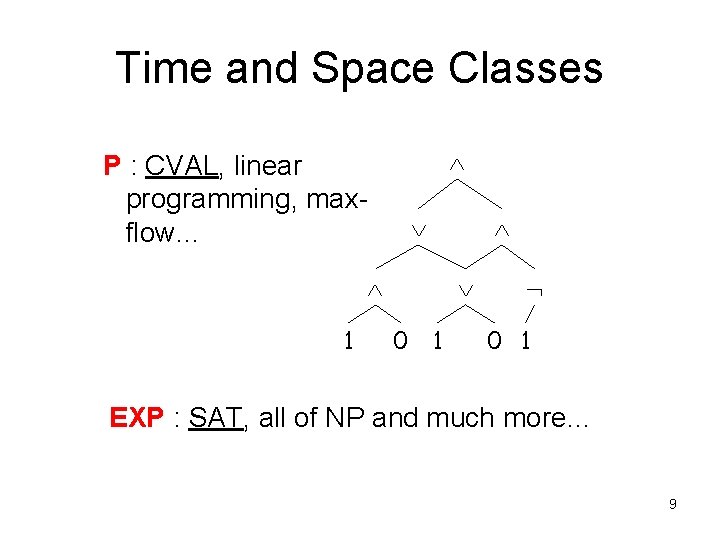
Time and Space Classes P : CVAL, linear programming, maxflow… 1 0 1 EXP : SAT, all of NP and much more… 9

Relationships between classes • How are these four classes related to each other? • Time Hierarchy Theorem implies P ⊊ EXP – P ⊊ TIME(2 n) ( TIME(2(2 n)3) ⊆ EXP • Space Hierarchy Theorem implies L ⊊ PSPACE – L = SPACE(log n) ⊊ SPACE(log 2 n) ⊊ PSPACE 10

Relationships between classes • Easy: P ⊆ PSPACE • L vs. P, PSPACE vs. EXP ? 11

Relationships between classes • Useful convention: Turing Machine configurations. Any point in computation σ1 σ2 … σi σi+1 … σm . . . state = q represented by string: C = σ1 σ2 … σi q σi+1 σi+2… σm • start configuration for single-tape TM on input x: qstartx 1 x 2…xn 12

Relationships between classes • easy to tell if C yields C’ in 1 step • configuration graph: nodes are configurations, edge (C, C’) iff C yields C’ in one step • # configurations for a 2 -tape TM (work tape + read-only input) that runs in space S(n) n x S(n) x |Q| x |∑|S(n) input-tape head position state work-tape head position work-tape contents 13

Relationships between classes • if S(n) = c log n, at most n x (c log n) x c 0 x c 1 c log n ≤ nk configurations. • can determine if reach qaccept or qreject from start configuration by exploring config. graph of size nk (e. g. by DFS) • Conclude: L ⊆ P 14

Relationships between classes • if S(n) = nc, at most c k n n c n x c 0 x c 1 ≤ 2 configurations. • can determine if reach qaccept or qreject from start configuration by exploring config. k n graph of size 2 (e. g. by DFS) • Conclude: PSPACE ⊆ EXP 15

Relationships between classes • So far: L ⊆ PSPACE ⊆ EXP • • believe all containments strict know PSPACE ⊊ L know EXP ⊊ P Two major unsolved problems: ? L=P ? P = PSPACE 16

Summary • nondeterministic time classes: NP, co. NP, NEXP • NTIME Hierarchy Theorem: NP ≠ NEXP • major open questions: ? P = NP ? NP = co. NP 17

Summary • NP-“intermediate” problems (unless P = NP) – technique: delayed diagonalization • unary languages not NP-complete (unless P = NP) – true for sparse languages as well (homework) • complete problems: – circuit SAT is NP-complete – UNSAT is co. NP-complete – succinct circuit SAT is NEXP-complete 18

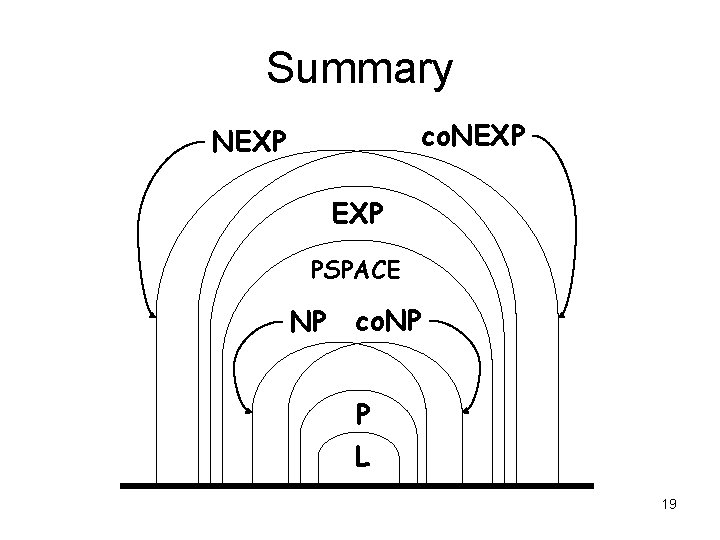
Summary co. NEXP EXP PSPACE NP co. NP P L 19