Ultimate Strength Analysis of Arbitrary Cross Sections under

Ultimate Strength Analysis of Arbitrary Cross Sections under Biaxial Bending and Axial Load by Fiber Model and Curvilinear Polygons Aristotelis Charalampakis and Vlasis Koumousis National Technical University of Athens Institute of Structural Analysis and Aseismic Research 1

National Technical University of Athens Problem definition Task: Analysis of arbitrary cross sections under biaxial bending and axial load Using a “fiber model” based on the Bernoulli – Euler assumption: Ø Simple calculation of strains (plane sections remain plane) Ø Used in Design Codes Ø Close agreement with experimental results for monotonic / proportional loading Ø Moment – curvature diagram, interaction curves and failure surfaces can be used in non-linear analyses 2

National Technical University of Athens Cross Section Arbitrary Cross Section Ø defined by curvilinear polygons (i. e. polygons with edges that may be straight lines or arcs) Ø the polygons can be nested to any depth 3

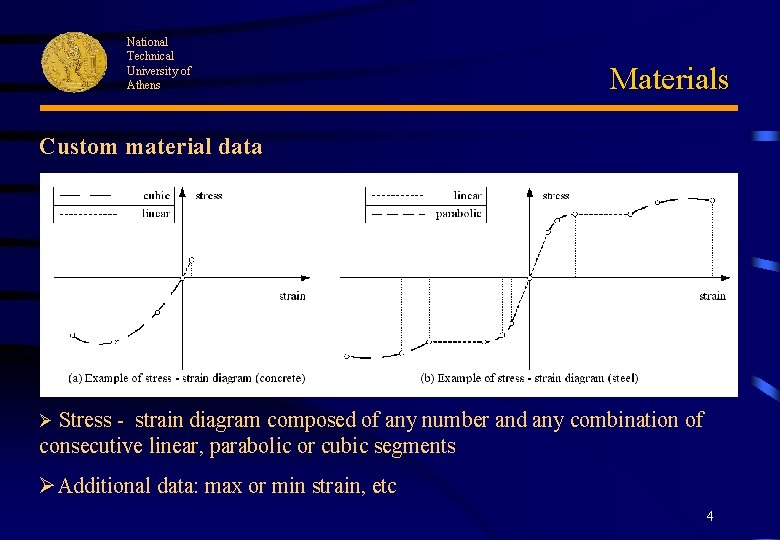
National Technical University of Athens Materials Custom material data Ø Stress - strain diagram composed of any number and any combination of consecutive linear, parabolic or cubic segments ØAdditional data: max or min strain, etc 4

National Technical University of Athens Materials Ø “Foreground” and “Background” materials for each curvilinear polygon. Positive “Foreground” / Negative “Background” material stresses 5

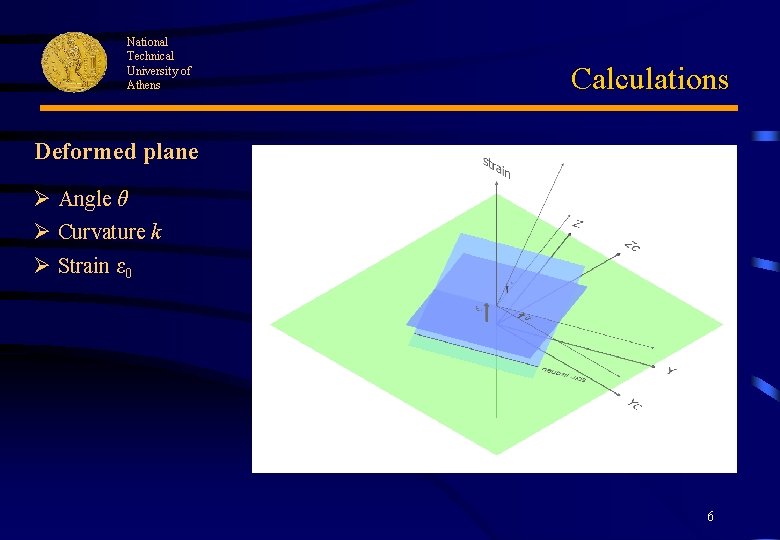
National Technical University of Athens Calculations Deformed plane Ø Angle θ Ø Curvature k Ø Strain ε 0 6

National Technical University of Athens Calculations Ø Direction of neutral axis (angle θ) is imposed by the algorithm Ø By rotating the cross section by this angle θ, strains (and stresses) vary only in vertical axis Z: ØNeutral axis is parallel to horizontal axis Y: 7

National Technical University of Athens Calculations Trapezoidal decomposition of curvilinear polygons Ø Basic set of curvilinear trapezoids calculated only once per angle θ 8

National Technical University of Athens Calculations Basic integrals Ø Basic integrals calculated only once per curvilinear trapezoid 9

National Technical University of Athens Calculations Stress resultants for a curvilinear trapezoid Cubic stress – strain segment (αi material constants). Strain distribution in current deformed plane (θ fixed). ØBasic integrals Ij(m, n) have already been calculated. Independent of k, ε 0. ØSummation over the trapezoids produces the overall stress resultants. 10

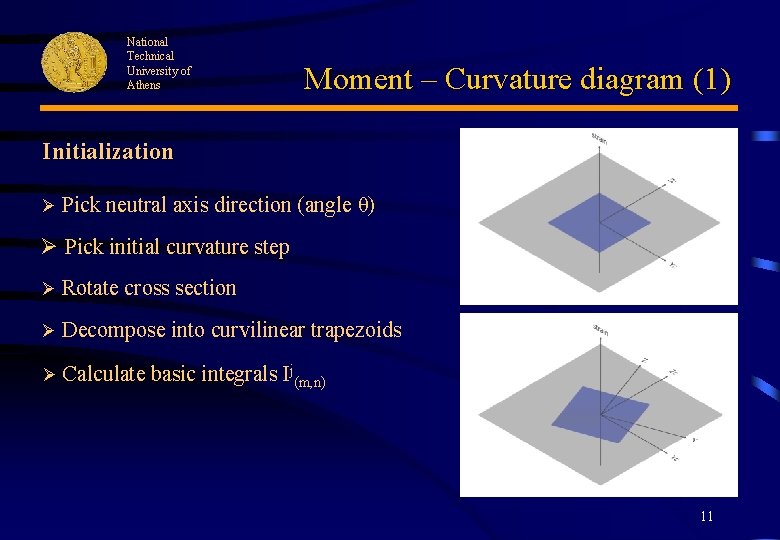
National Technical University of Athens Moment – Curvature diagram (1) Initialization Ø Pick neutral axis direction (angle θ) Ø Pick initial curvature step Ø Rotate cross section Ø Decompose into curvilinear trapezoids Ø Calculate basic integrals Ij(m, n) 11

National Technical University of Athens Moment – Curvature diagram (2) Ø Calculate initial ε 0 for axial equilibrium with no curvature 12

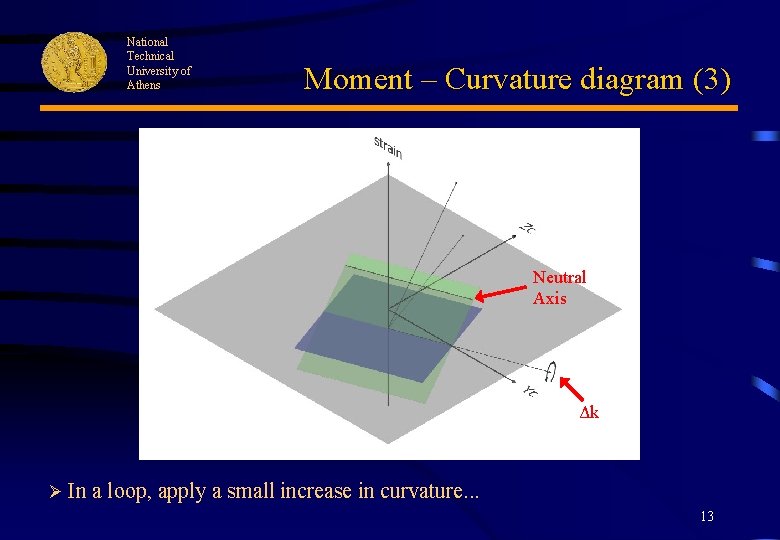
National Technical University of Athens Moment – Curvature diagram (3) Neutral Axis Δk Ø In a loop, apply a small increase in curvature. . . 13

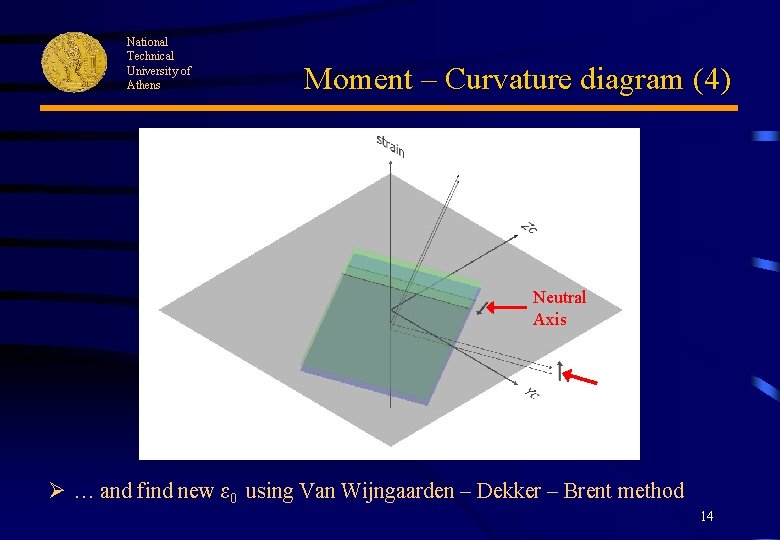
National Technical University of Athens Moment – Curvature diagram (4) Neutral Axis Ø … and find new ε 0 using Van Wijngaarden – Dekker – Brent method 14

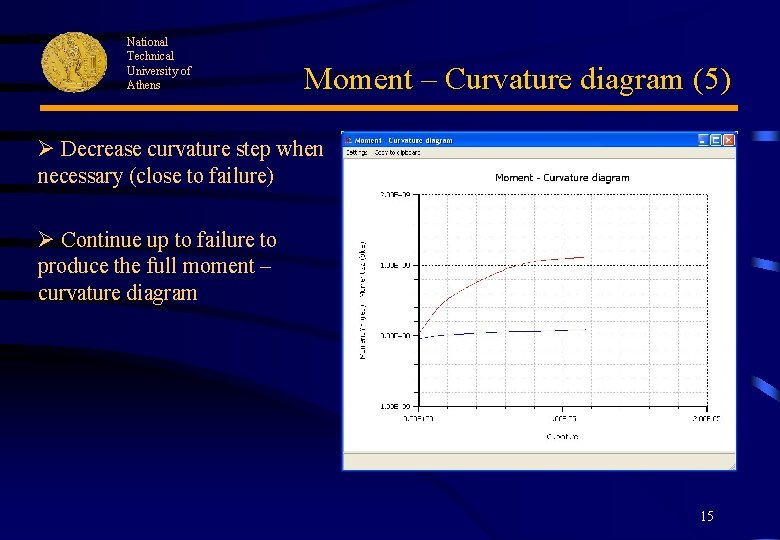
National Technical University of Athens Moment – Curvature diagram (5) Ø Decrease curvature step when necessary (close to failure) Ø Continue up to failure to produce the full moment – curvature diagram 15

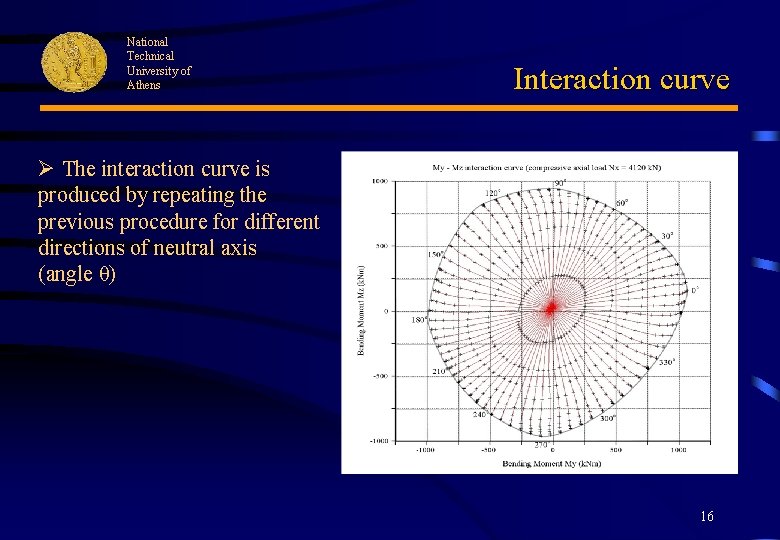
National Technical University of Athens Interaction curve Ø The interaction curve is produced by repeating the previous procedure for different directions of neutral axis (angle θ) 16

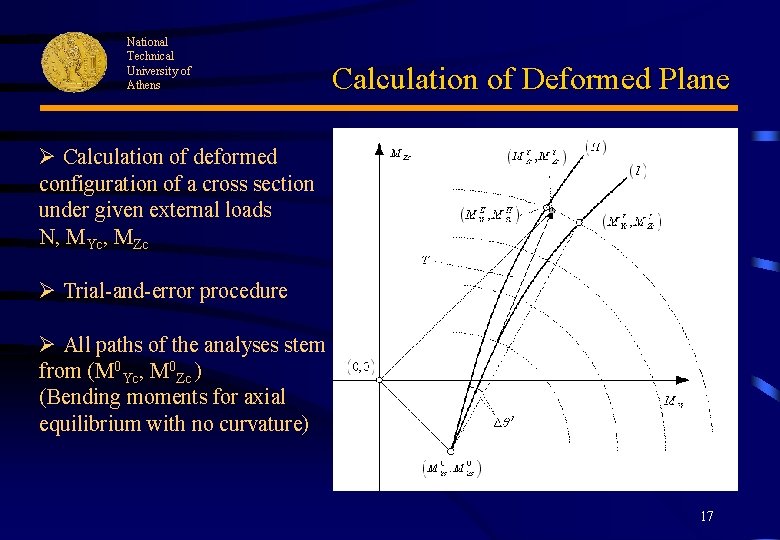
National Technical University of Athens Calculation of Deformed Plane Ø Calculation of deformed configuration of a cross section under given external loads N, MYc, MZc Ø Trial-and-error procedure Ø All paths of the analyses stem from (M 0 Yc, M 0 Zc ) (Bending moments for axial equilibrium with no curvature) 17

National Technical University of Athens Example 1 EC 2 design charts Ø Rectangular cross section ØEqual reinforcement, top and bottom ØSteel grade S 500 Ød 1/h = 0. 10 Ø Calculations for : ω = 0. 00, 0. 50, 1. 00, 1. 50, 2. 00 and various axial load levels 18

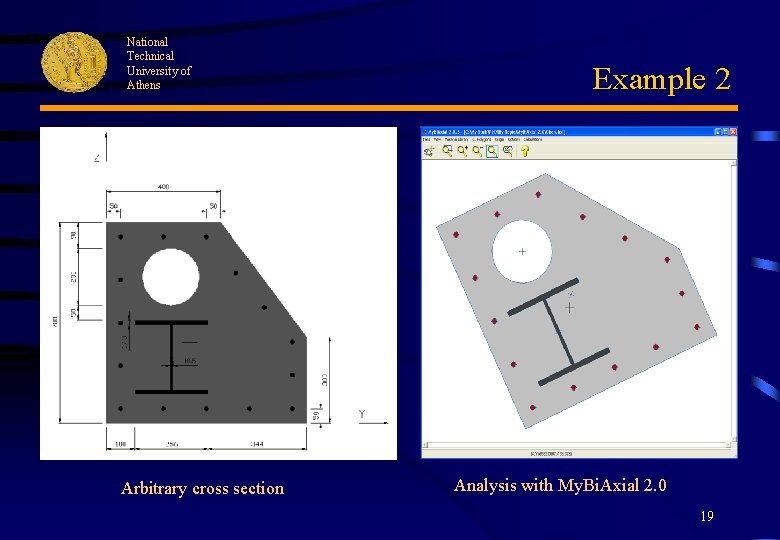
National Technical University of Athens Arbitrary cross section Example 2 Analysis with My. Bi. Axial 2. 0 19

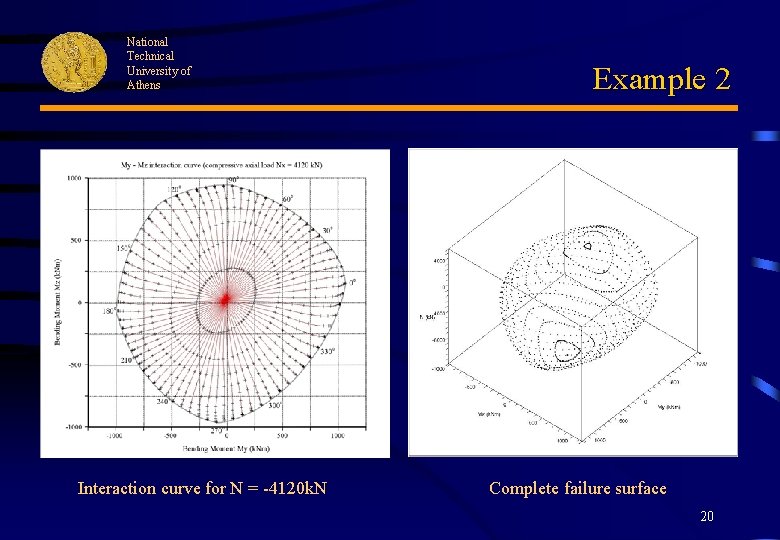
National Technical University of Athens Interaction curve for N = -4120 k. N Example 2 Complete failure surface 20

National Technical University of Athens Example 3 Bolted connection 3 D view of proposed connection 21

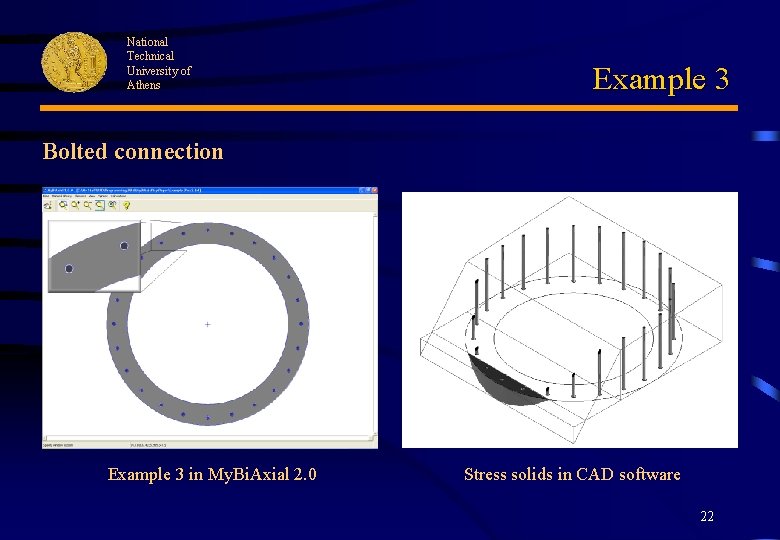
National Technical University of Athens Example 3 Bolted connection Example 3 in My. Bi. Axial 2. 0 Stress solids in CAD software 22

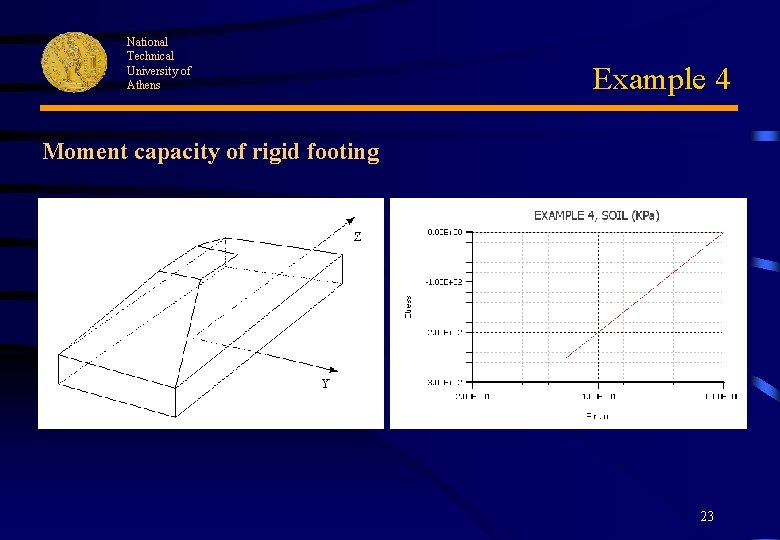
National Technical University of Athens Example 4 Moment capacity of rigid footing 23

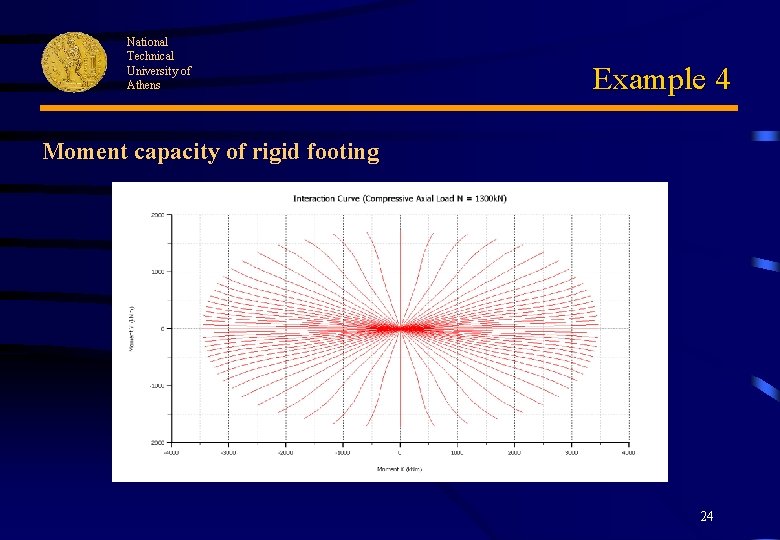
National Technical University of Athens Example 4 Moment capacity of rigid footing 24

National Technical University of Athens Conclusions Ø Generic algorithm for the analysis of arbitrary cross sections under biaxial bending and axial load Ø Features: § Custom material data § Curved graphical objects with analytical expressions instead of approximations with simple polygons or dimensionless fibers for the reinforcement bars § Construction of full bending moment – curvature diagram § Fast, very stable algorithm § Can be used for a variety of purposes as demonstrated in the examples 25