UKURAN VARIASI ATAU DISPERSI Pengukuran Dispersi KONSEP DASAR

UKURAN VARIASI ATAU DISPERSI (Pengukuran Dispersi)

KONSEP DASAR • Dispersi = Variasi data = Keragaman data • Definisi Dispersi adalah data yang menggambarkan bagaimana suatu kelompok data menyebar terhadap pusatnya data atau ukuran penyebaran suatu kelompok data terhadap pusat data 2

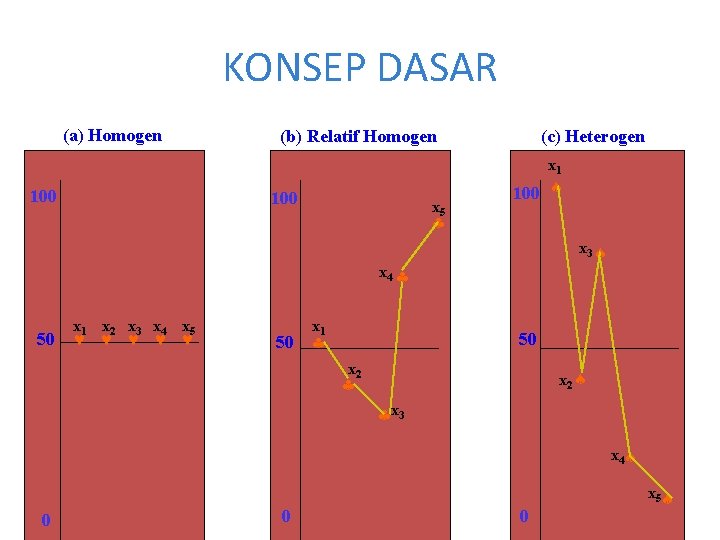
KONSEP DASAR Contoh Tiga kelompok data terdiri dari: a. 50, 50, 50 (homogen) rata-rata hitung = 50 b. 50, 40, 30, 60, 70 (heterogen) rata-rata hitung = 50 c. 100, 40, 80, 20, 10 (heterogen) rata-rata hitung = 50 Kelompok c lebih heterogen dibandingkan b 3

KONSEP DASAR (a) Homogen (b) Relatif Homogen (c) Heterogen x 1 100 x 5 100 x 3 x 4 x 1 x 2 x 3 x 4 x 5 50 x 1 50 x 2 x 3 x 4 0 0 0 x 5 4

KONSEP DASAR Jenis 1. Dispersi Mutlak Dispersi mutlak digunakan untuk mengetahui tingkat variabilitas nilai-nilai observasi pada suatu data 2. Dispersi Relatif Dispersi relatif digunakan untuk membandingkan tingkat variabilitas nilai-nilai observasi suatu data dengan tingkat variabilitas nilai-nilai observasi data lainnya. 5

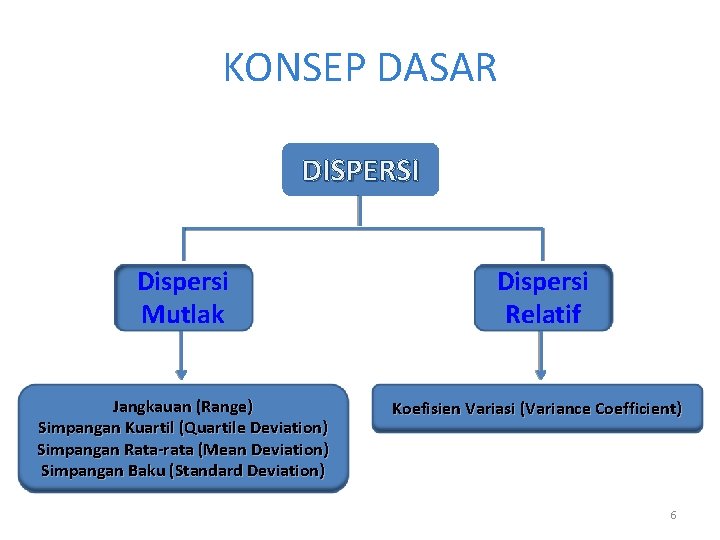
KONSEP DASAR DISPERSI Dispersi Mutlak Jangkauan (Range) Simpangan Kuartil (Quartile Deviation) Simpangan Rata-rata (Mean Deviation) Simpangan Baku (Standard Deviation) Dispersi Relatif Koefisien Variasi (Variance Coefficient) 6

ALASAN MEMPELAJARI DISPERSI q Mean dan median hanya menggambarkan pusat data dari sekelompok data, tetapi tidak menggambarkan penyebaran nilai pada data tersebut. q Dua kelompok data dengan mean yang sama, belum tentu memiliki penyebaran data yang sama. q Ukuran dispersi yang kecil menunjukkan nilai data saling berdekatan (perbedaan kecil), sedangkan ukuran dispersi yang besar menunjukkan nilai data saling menyebar (perbedaan nilai masing-masing data besar). q Ukuran dispersi digunakan untuk melengkapi perhitungan nilai pusat data. 7

JENIS DISPERSI • Dispersi Data Tunggal – Jangkauan – Simpangan Rata-rata – Simpangan Baku • Dispersi Data Berkelompok – Jangkauan – Simpangan Baku 8

Jangkauan – Data Tunggal Definisi Jangkauan adalah selisih antara nilai maksimum dengan nilai minimum dalam suatu kelompok/ susunan data. Lambang Jangkauan dapat ditulis “ r “ Nama Lain Nilai Jarak, dapat ditulis “ NJ ” 9

Jangkauan – Data Tunggal Sifat Jangkauan merupakan ukuran keragaman yang paling sederhana. Jangkauan sangat peka terhadap data dengan nilai terbesar dan nilai terkecil. Semakin kecil nilai r maka kualitas data akan semakin baik, sebaliknya semakin besar nilai r, maka kualitasnya semakin tidak baik. 10

Jangkauan – Data Tunggal Rumus r = Xn – X 1 r = Nilai Maksimum – Nilai Minimum Contoh Diketahui data 20, 30, 50, 70, 100. Tentukan nilai jangkauan data. r = X 5 – X 1 r = 100 – 20 r = 80 11

Jangkauan – Data Berkelompok Rumus r = Nilai tengah kelas terakhir – Nilai tengah kelas pertama r = Batas kelas terakhir – Batas bawah kelas pertama 12

Jangkauan – Data Berkelompok • Contoh Data berat badan 100 mahasiswa suatu perguruan tinggi. Tentukan nilai jarak dari data tersebut. Berat badan (Kg) 60 63 66 69 72 – – – 62 65 68 71 74 Banyaknya Mahasiswa (f) 5 18 42 27 8 13

Jangkauan – Data Berkelompok Jawaban Cara I Nilai tengah kelas pertama = (60 + 62) : 2 Nilai tengah kelas pertama = 61 Nilai tengah kelas terakhir = (72 + 74) : 2 Nilai tengah kelas terakhir = 73 r = Nilai tengah kelas terakhir – Nilai tengah kelas pertama r = 73 – 61 r = 12 14

Jangkauan – Data Berkelompok Jawaban Cara II Batas bawah kelas pertama = 60 – 0, 5 = 59, 5 Batas kelas terakhir = 74 + 0, 5 = 74, 5 r = Batas kelas terakhir – Batas bawah kelas pertama r = 74, 5 – 59, 5 r = 15 Catatan : Cara 1 cenderung menghilangkan kasus ekstrim 15

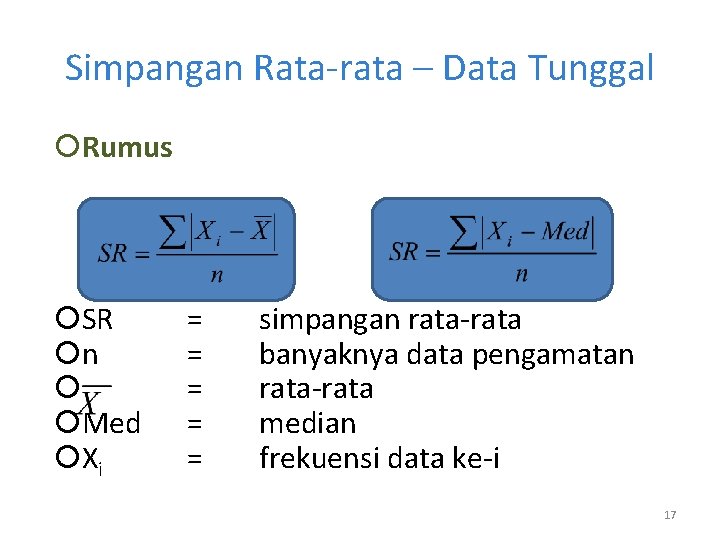
Simpangan Rata-rata – Data Tunggal Definisi Simpangan rata-rata adalah jumlah nilai mutlak dari selisih semua nilai dengan nilai rata-rata dibagi dengan banyaknya data. Lambang Simpangan rata-rata dapat ditulis “ SR “ 16

Simpangan Rata-rata – Data Tunggal Rumus SR n Med Xi = = = simpangan rata-rata banyaknya data pengamatan rata-rata median frekuensi data ke-i 17

Simpangan Rata-rata – Data Tunggal • Contoh Diketahui data 30, 40, 50, 60, 70. Tentukan simpangan rata-rata dan simpangan median. • Jawaban 18

Simpangan Rata-rata – Data Tunggal • Simpangan rata-rata 19

Simpangan Rata-rata – Data Tunggal • Simpangan Median 20

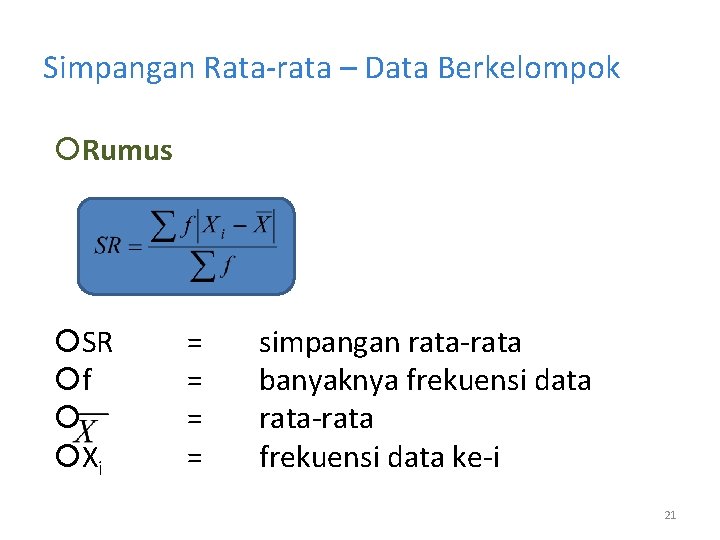
Simpangan Rata-rata – Data Berkelompok Rumus SR f Xi = = simpangan rata-rata banyaknya frekuensi data rata-rata frekuensi data ke-i 21

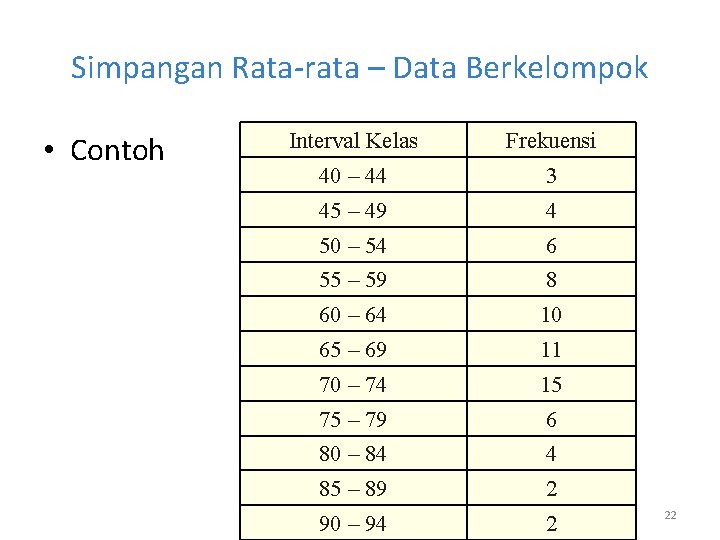
Simpangan Rata-rata – Data Berkelompok • Contoh Interval Kelas Frekuensi 40 – 44 3 45 – 49 4 50 – 54 6 55 – 59 8 60 – 64 10 65 – 69 11 70 – 74 15 75 – 79 6 80 – 84 4 85 – 89 2 90 – 94 2 22

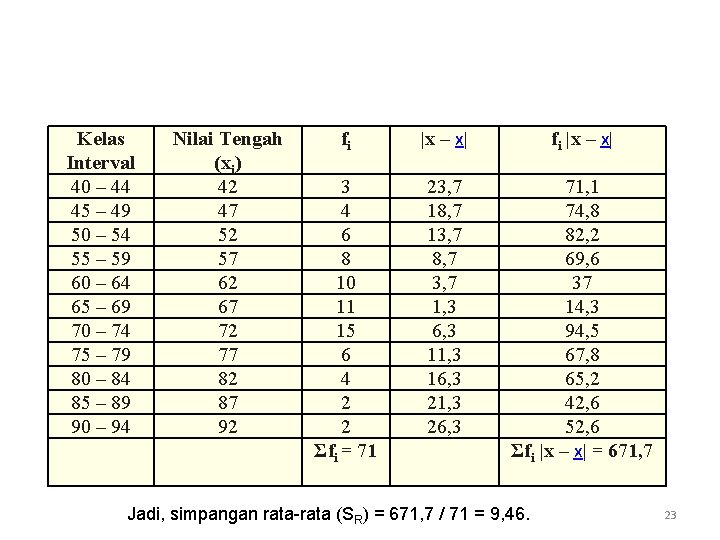
Kelas Interval 40 – 44 45 – 49 50 – 54 55 – 59 60 – 64 65 – 69 70 – 74 75 – 79 80 – 84 85 – 89 90 – 94 Nilai Tengah (xi) 42 47 52 57 62 67 72 77 82 87 92 fi |x – x| 3 4 6 8 10 11 15 6 4 2 2 Σfi = 71 23, 7 18, 7 13, 7 8, 7 3, 7 1, 3 6, 3 11, 3 16, 3 21, 3 26, 3 71, 1 74, 8 82, 2 69, 6 37 14, 3 94, 5 67, 8 65, 2 42, 6 52, 6 Σfi |x – x| = 671, 7 Jadi, simpangan rata-rata (SR) = 671, 7 / 71 = 9, 46. 23

Hitung simpangan rata-rata dari data kuantitatif berikut 12, 3, 11, 3, 4, 7, 5, 11 24

VARIANS Definisi Varians adalah ukuran keragaman yang melibatkan seluruh data. Varians merupakan rata-rata kuadrat selisih dari semua nilai data terhadap nilai rata-rata hitung. Varians didasarkan pada perbedaan antara nilai tiap observasi (Xi) dan rata-rata ( untuk sampel dan untuk populasi) 25

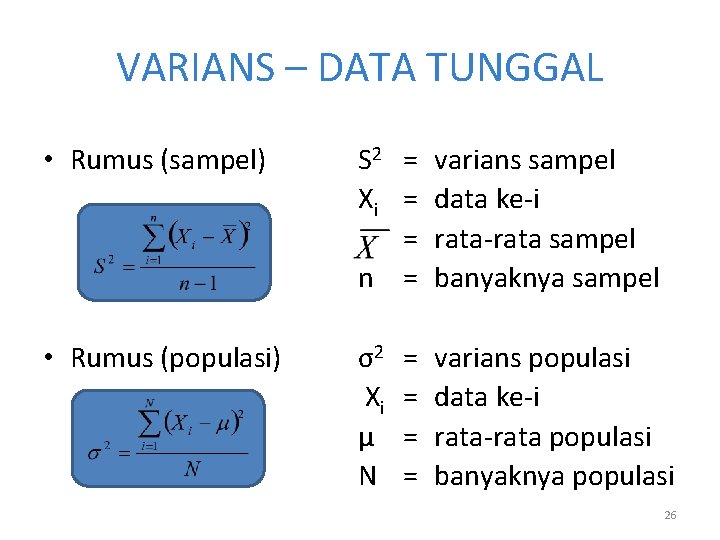
VARIANS – DATA TUNGGAL • Rumus (sampel) S 2 = varians sampel Xi = data ke-i = rata-rata sampel n = banyaknya sampel • Rumus (populasi) σ2 Xi μ N = = varians populasi data ke-i rata-rata populasi banyaknya populasi 26

VARIANS – DATA BERKELOMPOK • Rumus (sampel) S 2 = varians sampel Xi = nilai tengah kelas ke-i fi = frekuensi kelas ke-i = rata-rata sampel • Rumus (populasi) σ2 Xi fi μ = = varians populasi nilai tengah kelas ke-i frekuensi kelas ke-i rata-rata populasi 27

Simpangan Baku – Data Tunggal Definisi Simpangan baku adalah akar kuadrat positif dari varians. Simpangan baku diukur pada satuan data yang sama, sehingga mudah untuk diperbandingkan. Simpangan baku paling banyak digunakan karena mempunyai sifat-sifat matematis yang sangat penting dan berguna untuk pembahasan teori dan analisis. 28

Simpangan Baku – Data Tunggal Lambang Simpangan baku dapat ditulis “ S “ Nama Lain Standar Deviasi, dapat ditulis “ SD “ Kelompok data yang heterogen mempunyai simpangan baku yang besar. Simpangan baku populasi (σ) sering dipakai. 29

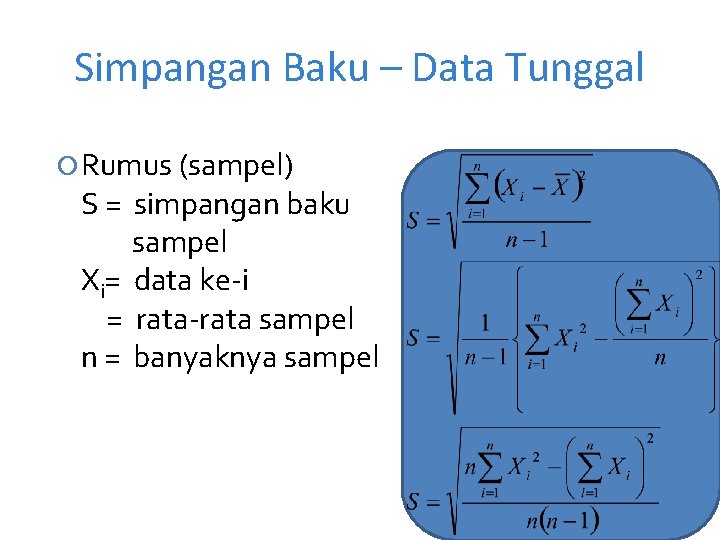
Simpangan Baku – Data Tunggal Rumus (sampel) S = simpangan baku sampel Xi= data ke-i = rata-rata sampel n = banyaknya sampel 30

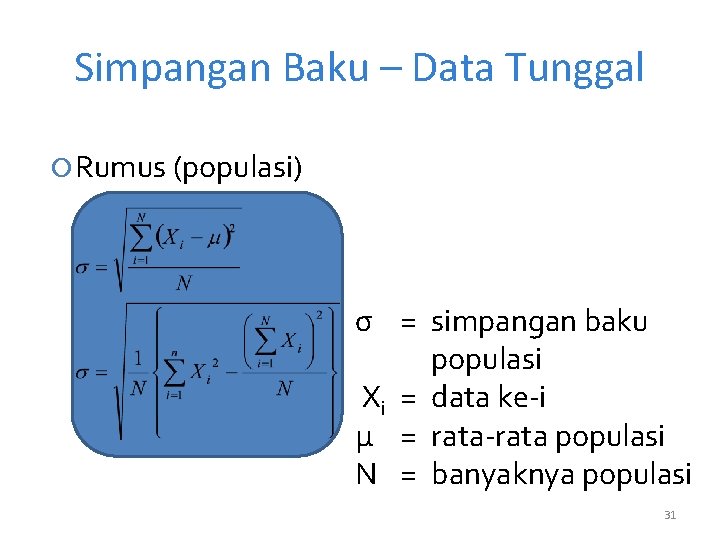
Simpangan Baku – Data Tunggal Rumus (populasi) σ = simpangan baku populasi Xi = data ke-i μ = rata-rata populasi N = banyaknya populasi 31

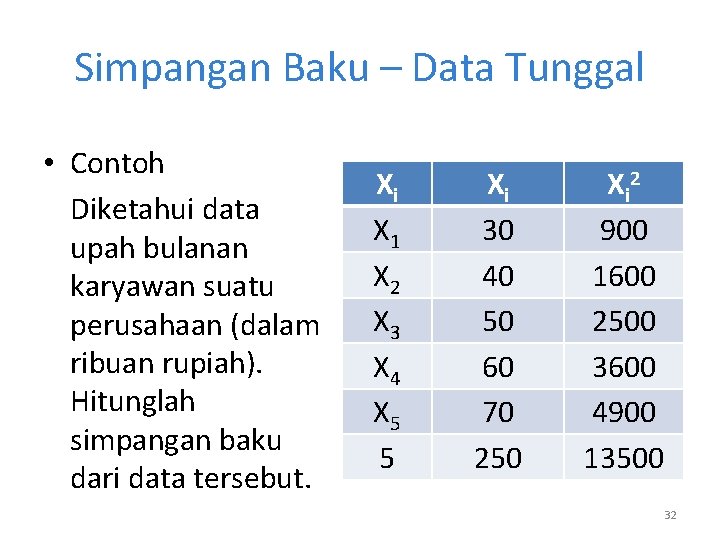
Simpangan Baku – Data Tunggal • Contoh Diketahui data upah bulanan karyawan suatu perusahaan (dalam ribuan rupiah). Hitunglah simpangan baku dari data tersebut. Xi X 1 X 2 X 3 X 4 X 5 5 Xi 30 40 50 60 70 250 X i 2 900 1600 2500 3600 4900 13500 32

Simpangan Baku – Data Tunggal Jawaban Jadi simpangan baku dari data tersebut adalah 14, 14 (Rp 14. 140, 00) 33

Simpangan Baku – Data Berkelompok Rumus simpangan baku populasi (umum) σ = Mi = k μ = N = simpangan baku populasi nilai tengah dari kelas ke-i, i = 1, 2, …, rata-rata populasi banyaknya populasi 34

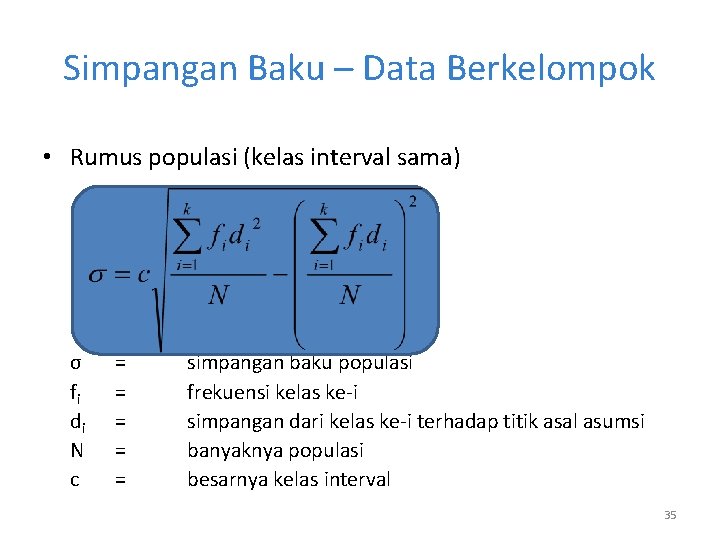
Simpangan Baku – Data Berkelompok • Rumus populasi (kelas interval sama) σ fi di N c = = = simpangan baku populasi frekuensi kelas ke-i simpangan dari kelas ke-i terhadap titik asal asumsi banyaknya populasi besarnya kelas interval 35

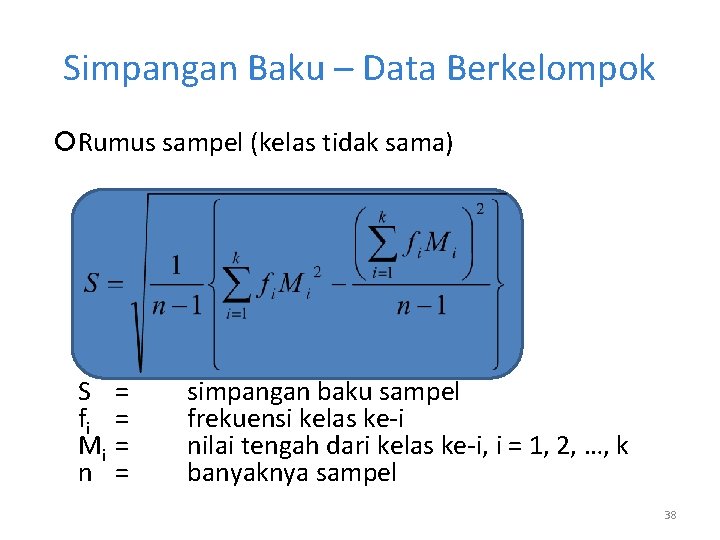
Simpangan Baku – Data Berkelompok Rumus populasi (kelas interval tidak sama) σ fi Mi N = = simpangan baku populasi frekuensi kelas ke-i nilai tengah dari kelas ke-i, i = 1, 2, …, k banyaknya populasi 36

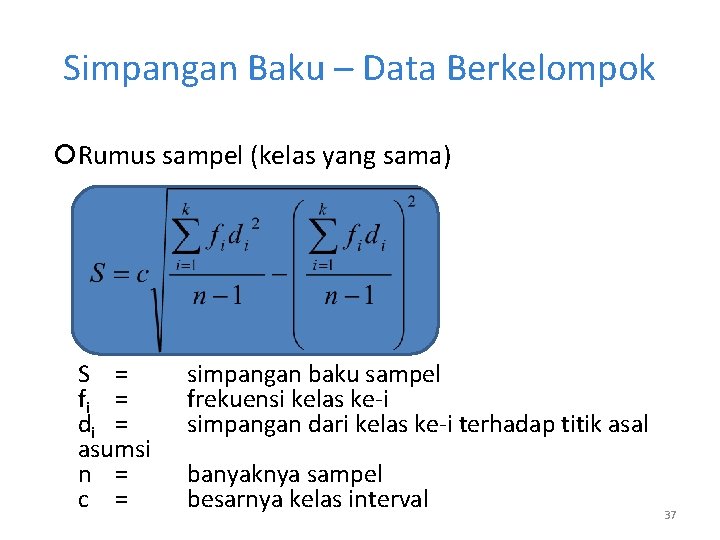
Simpangan Baku – Data Berkelompok Rumus sampel (kelas yang sama) S = fi = di = asumsi n = c = simpangan baku sampel frekuensi kelas ke-i simpangan dari kelas ke-i terhadap titik asal banyaknya sampel besarnya kelas interval 37

Simpangan Baku – Data Berkelompok Rumus sampel (kelas tidak sama) S fi Mi n = = simpangan baku sampel frekuensi kelas ke-i nilai tengah dari kelas ke-i, i = 1, 2, …, k banyaknya sampel 38

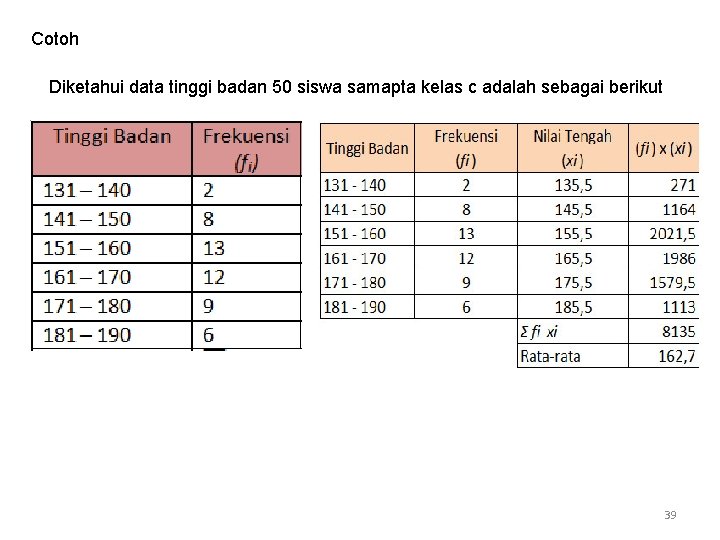
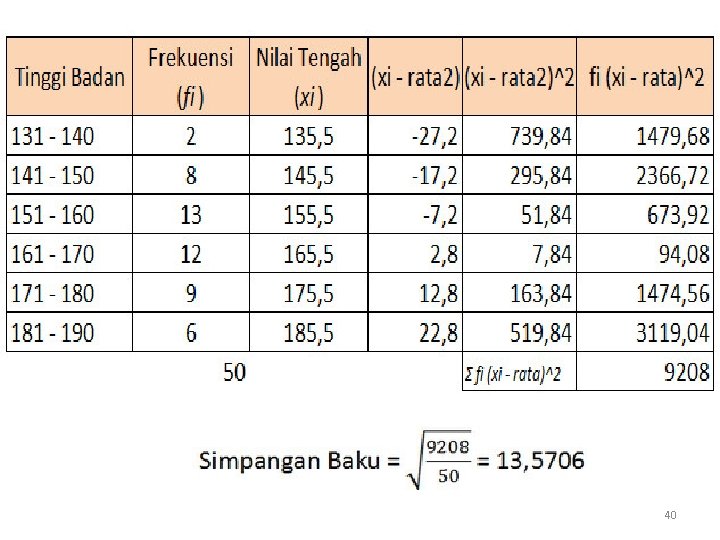
Cotoh Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut 39

40

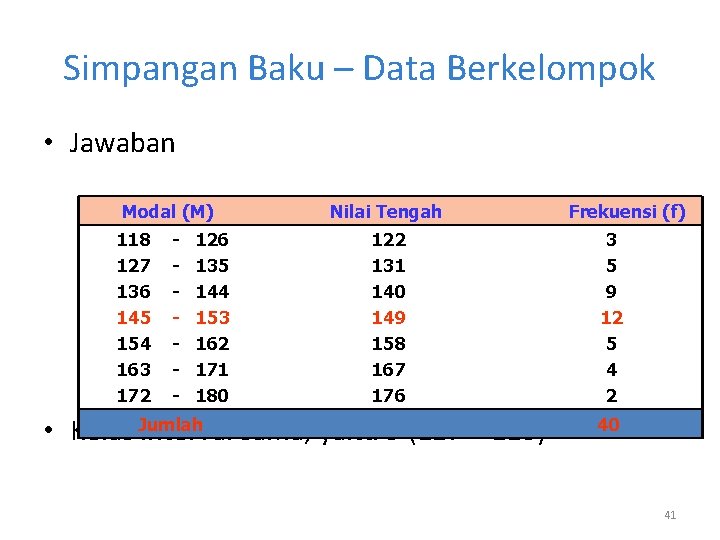
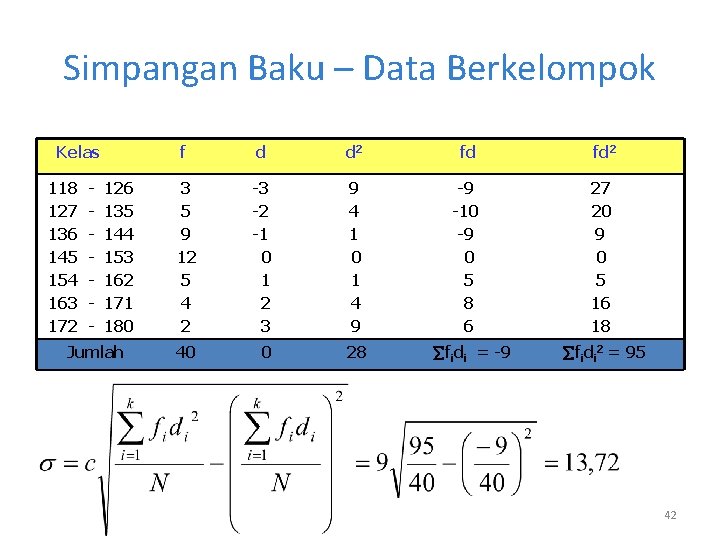
Simpangan Baku – Data Berkelompok • Jawaban Modal (M) 118 127 136 145 154 163 172 - 126 135 144 153 162 171 180 Nilai Tengah 122 131 140 149 158 167 176 • Kelas Jumlah interval sama, yaitu 9 (127 – 118) Frekuensi (f) 3 5 9 12 5 4 2 40 41

Simpangan Baku – Data Berkelompok Kelas 118 127 136 145 154 163 172 - 126 135 144 153 162 171 180 Jumlah f d d 2 fd fd 2 3 5 9 12 5 4 2 -3 -2 -1 0 1 2 3 9 4 1 0 1 4 9 -9 -10 -9 0 5 8 6 27 20 9 0 5 16 18 40 0 28 fidi = -9 fidi 2 = 95 42

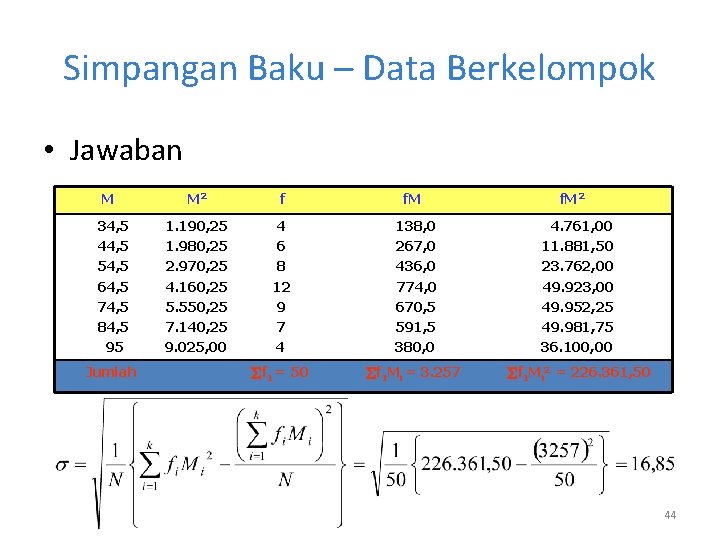
Simpangan Baku – Data Berkelompok • Contoh Data nilai ujian statistik dasar dari 50 mahasiswa STMIK MDP, disusun dalam tabel berikut ini. Tentukan simpangan baku dari data di samping. Kelas M (Nilai Tengah) f 30 40 50 60 70 80 90 34, 5 44, 5 54, 5 64, 5 74, 5 84, 5 94, 5 4 6 8 12 9 7 4 - 39 49 59 69 79 89 100 43

Simpangan Baku – Data Berkelompok • Jawaban M 34, 5 44, 5 54, 5 64, 5 74, 5 84, 5 95 Jumlah M 2 f f. M 2 1. 190, 25 1. 980, 25 2. 970, 25 4. 160, 25 5. 550, 25 7. 140, 25 9. 025, 00 4 6 8 12 9 7 4 138, 0 267, 0 436, 0 774, 0 670, 5 591, 5 380, 0 4. 761, 00 11. 881, 50 23. 762, 00 49. 923, 00 49. 952, 25 49. 981, 75 36. 100, 00 f 1 = 50 f 1 Mi = 3. 257 f 1 Mi 2 = 226. 361, 50 44

Soal-soal Sepuluh orang juri memberikan penilaian terhadap jenis makanan yang baru dikembangkan sebagai berikut. 23 30 14 10 15 28 30 25 24 17 Hitunglah nilai jangkauan, simpangan rata-rata, dan simpangan baku. 45