Ukuran Penyebaran Data Rentang rentang antar kuartil simpangan

Ukuran Penyebaran Data Rentang, rentang antar kuartil, simpangan rata-rata, varians dan standar deviasi, koefisien variasi

Ukuran Penyebaran Data • Ukuran statistik menggambarkan pencaran data kuantitatif • Ukuran simpangan (ukuran dispersi) atau ukuran variasi (ukuran keseragaman) • Mengukur penyimpangan nilai-nilai data disekitar nilai rata-rata • Makin kecil bilangan data makin seragam

Rentang, RAK, SK Rentang/Jangkauan (R) R= data maks– data min Rentang Antar Kuartil RAK = Q 3 – Q 1 (RAK) Simpangan Kuartil SK = ½ RAK (SK)/Rentang Semi = ½ (Q 3 – Q 1) Antar Kuartil • Hitung R, RAK, dan SK dari data berikut : 2, 4, 5, 6, 8, 9, 12

Data Berkelompok Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30 Tentukan Rentang Antar Kuartil dan Simpangan Kuartil

Simpangan Rata-rata Populasi Data Tunggal Sampel Berapa simpangan rata-rata dari data berikut : 2, 5, 6, 8, 9 ? Nilai 2 5 6 8 9

Simpangan Rata-rata Data Berkelompok Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30 mi 52, 5 58, 5 64, 5 70, 5 76, 5 82, 5 - -

Varians & Standar Deviasi Populasi Varians Populasi Standar Deviasi Sampel (Metode Deviasi Pangkat Dua) xi 2 5 6 8 9 - (Metode Rata-rata Pangkat Dua) Hitung varians dan standar deviasi dari data 2, 5, 6, 8, 9

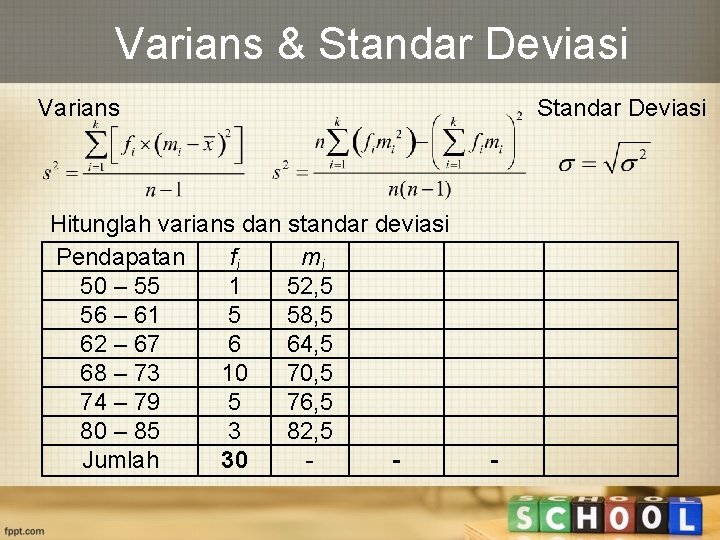
Varians & Standar Deviasi Varians Hitunglah varians dan standar deviasi Pendapatan fi mi 50 – 55 1 52, 5 56 – 61 5 58, 5 62 – 67 6 64, 5 68 – 73 10 70, 5 74 – 79 5 76, 5 80 – 85 3 82, 5 Jumlah 30 - Standar Deviasi -

Rumus Perkiraan Varians & Standar Deviasi Dengan Metode Short Cut Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30 mi 52, 5 58, 5 64, 5 70, 5 76, 5 82, 5 - - -

Koefisien Variasi • Memeriksa keseragaman data yang berbeda satuan • Tidak bergantung pada satuan

Koefisien Variasi • Contoh 5. 5 Data berikut menunjukan umur dan pendapatan 5 orang karyawan di sebuah perusahaan X : Manakah yang lebih seragam, umur atau pendapatan karyawan? Tabel 5. 4 Data Mengenai Umur & Pendapatan 5 Orang Karyawan 1 2 3 4 5 Umur ( Tahun ) 34 27 37 32 25 Pendapatan ( $ ) 75 90 123 187 135

Nilai Baku (Skor z) Contoh • Budi memperoleh nilai 83 pada UAS Statistik, dimana rata-rata kelas dan simpangan bakunya masing-masing 75 dan 12. Sedangkan pada UAS Kalkulus dimana rata-rata kelasnya 83 dan simpangan bakunya 16 ia memperoleh nilai 90. Dalam mata kuliah mana Budi mencapai kedudukan yang lebih baik?

Koefisien Kemiringan (Skewness) • Mengukur kemiringan atau kecondongan kurva • Sering disebut derajat kesimetrian Koefisien Kemiringan Pearson Tipe Pertama m = Me = Mo a. Simetris Koefisien Kemiringan Pearson Tipe Kedua Mo < Me < m b. Miring Positif m < Me < Mo c. Miring Negatif Hitung Koefisien kemiringan Pearson tipe satu dan dua dari data berkelompok pendapatan 30 toko komputer

Kurtosis • Ukuran untuk menentukan tinggi rendahnya puncak kurva • Ketinggian dibandingkan terhadap tinggi kurva distribusi normal. • Ukuran kurtosis disimbolkan dengan ” α 4 ”. leptokurtik (α 4>3), Tunggal mesokurtik (α 4=3), platikurtik (α 4<3), Berkelompok Diberikan data 2, 5, 6, 8, 9. hitunglah ukuran kurtosisnya !