Ukuran pemusatan data adalah ukuran untuk gambaran data

Ukuran pemusatan data adalah ukuran untuk gambaran data yang diambil dari sampel dan mewakili populasinya.

Ukuran pemusatan data adalah ukuran untuk gambaran data yang diambil dari sampel dan mewakili populasinya. Misalkan kumpulan data berikut adalah nilai uji kompetensi dasar dari 20 siswa kelas XI IPA.

Ukuran pemusatan data adalah ukuran untuk gambaran data yang diambil dari sampel dan mewakili populasinya. Misalkan kumpulan data berikut adalah nilai uji kompetensi dasar dari 20 siswa kelas XI IPA. 8 7 10 6 9 6 7 5 5 8 5 7 9 6 8 8 9 8 7 6 Dari kumpulan data yang belum diatas itu, kita tidak mempunyai gambaran atau kesimpulan apa-apa tentang nilai yang terdapat dalam kumpulan data tersebut. Ada tiga nilai statistik yang dapat digunakan untuk memberikan gambaran tentang kumpulan data di atas, yaitu rataan, median dan modus. Oleh karena itu rataan, median dan modus disebut sebagai ukuran pemusatan data atau ukuran tendensi sentral

a Mean ( x ) adalah nilai rata-rata suatu data yang diperoleh dari jumlah semua nilai datum dibagi dengan banyaknya data.

a Mean ( x ) adalah nilai rata-rata suatu data yang diperoleh dari jumlah semua nilai datum dibagi dengan banyaknya data. Data x 1, x 2, x 3, . . . xn x= x 1 + x 2 + x 3 +. . . + x n n Dimana : x = nilai rata-rata n = banyaknya data

a Mean ( x ) adalah nilai rata-rata suatu data yang diperoleh dari jumlah semua nilai datum dibagi dengan banyaknya data. Data x 1, x 2, x 3, . . . xn x= x 1 + x 2 + x 3 +. . . + x n n Dimana : x = nilai rata-rata n = banyaknya data Median (Me) adalah posisi nilai datum yang terletak di tengah setelah data diurutkan dari data terkecil hingga terbesar.

a Mean ( x ) adalah nilai rata-rata suatu data yang diperoleh dari jumlah semua nilai datum dibagi dengan banyaknya data. Data x 1, x 2, x 3, . . . xn x= x 1 + x 2 + x 3 +. . . + x n n Dimana : x = nilai rata-rata n = banyaknya data Median (Me) adalah posisi nilai datum yang terletak di tengah setelah data diurutkan dari data terkecil hingga terbesar. Jika n ganjil, maka : Me = Uru tan data ke - x 1( n+1) Jika n genap, maka : Me = Uru tan data ke - 12 æç x 1 n + x 1 n+1 ö÷ 2 è 2 ø 2

Modus (Mo) adalah nilai datum yang paling sering muncul atau nilai datum yang mempunyai frekuensi terbesar

Nilai raport seorang siswa pada semester ganjil adalah sebagai berikut : 7, 8, 8, 8, 9, 6, 6, 7, 8, 7 Tentukan nilai rata-rata, median dan modus dari nilai raport tersebut !

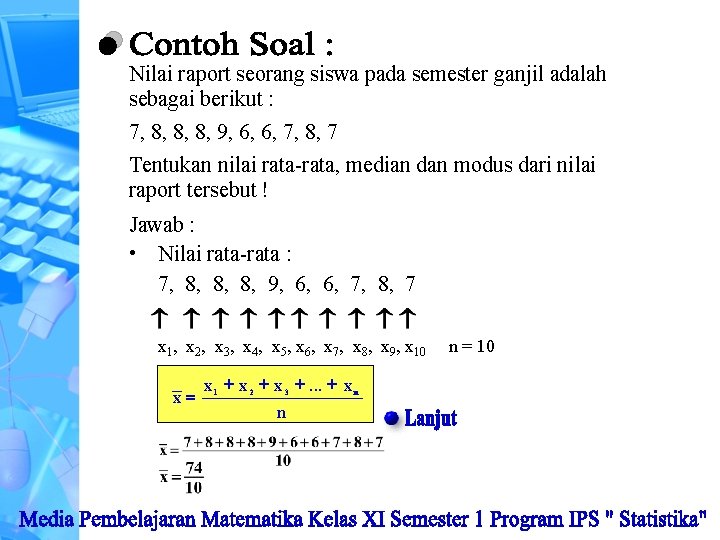
Nilai raport seorang siswa pada semester ganjil adalah sebagai berikut : 7, 8, 8, 8, 9, 6, 6, 7, 8, 7 Tentukan nilai rata-rata, median dan modus dari nilai raport tersebut ! Jawab : • Nilai rata-rata : 7, 8, 8, 8, 9, 6, 6, 7, 8, 7 x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10 x= x 1 + x 2 + x 3 +. . . + x n n n = 10

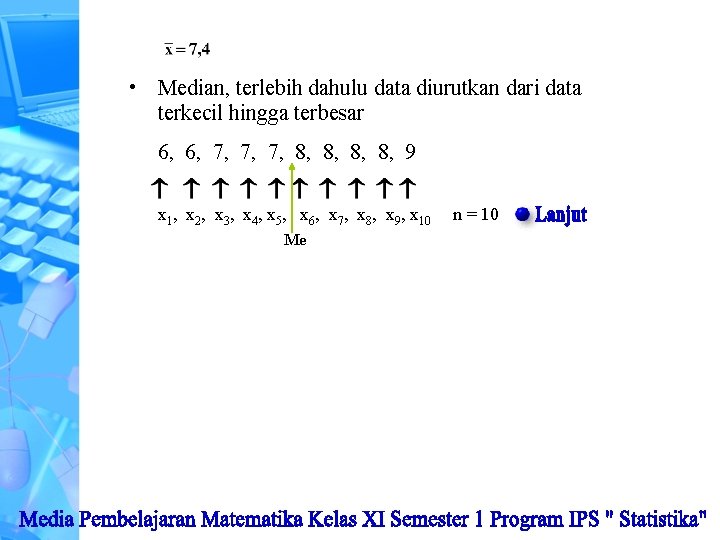
• Median, terlebih dahulu data diurutkan dari data terkecil hingga terbesar 6, 6, 7, 7, 7, 8, 8, 9 x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10 Me n = 10

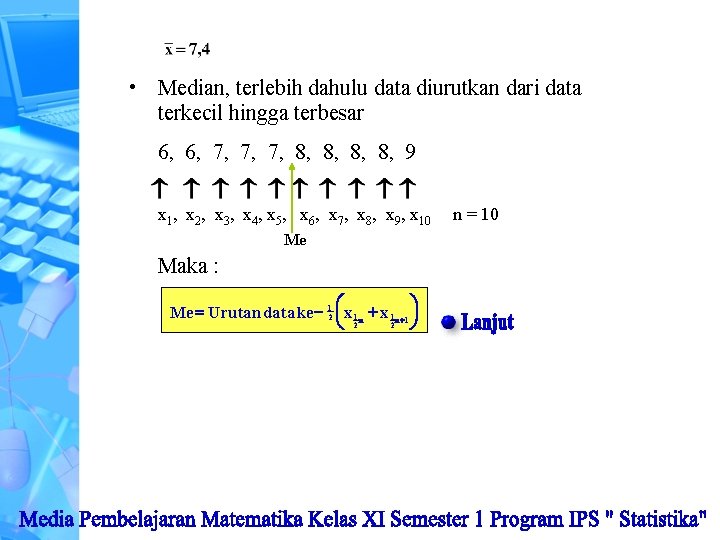
• Median, terlebih dahulu data diurutkan dari data terkecil hingga terbesar 6, 6, 7, 7, 7, 8, 8, 9 x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10 Me Maka : Me = Uru tan data ke - 12 æç x 1 n + x 1 n+1 ö÷ 2 è 2 ø n = 10

b Mean ( x ) x= å fix i å fi

b Mean ( x ) x= å fix i å fi Menggunakan Rataan Sementara : • Simpangan Rataan x = xs + å fixi å fi

b Mean ( x ) x= å fix i å fi Menggunakan Rataan Sementara : • Simpangan Rataan x = xs + å fixi å fi • Pengkodean (coding) æ å fiu i ö ÷I x = xs + ç è å fi ø

Median (Me) é 12 n - (å f )2 ù = + Me L 2 ê úI f 2 ë û L 2 n = = (å f ) = f 2 = I = 2 tepi bawah kelas yang memuat Me banyaknya data jumlah frekuensi sebelum Me frekuensi kelas yang memuat Me interval kelas

Median (Me) é 12 n - (å f )2 ù = + Me L 2 ê úI f 2 ë û L 2 n = = (å f ) = f 2 = I = 2 tepi bawah kelas yang memuat Me banyaknya data jumlah frekuensi sebelum Me frekuensi kelas yang memuat Me interval kelas Modus (Mo) æ d 1 ö ÷I Mo = L + ç + d d 2 ø è 1 L 2 d 1 d 2 I = = tepi bawah kelas yang memuat Mo selisih frekuensi kelas Mo dengan kelas sebelumnya selisih frekuensi kelas Mo dengan kelas sesudahnya interval kelas

Dari 80 orang guru yang mengikuti workshop Teknologi Informasi dan Komunikasi (TIK) dikelompokkan berdasarkan umur menjadi 5 kelas seperti terlihat pada tabel distribusi frekuensi berikut : Umur 30 – 34 35 – 39 40 – 44 45 – 49 50 - 54 Frekuensi 25 21 18 12 4 Tentukan : a. Umur rata-rata b. Median c. Modus

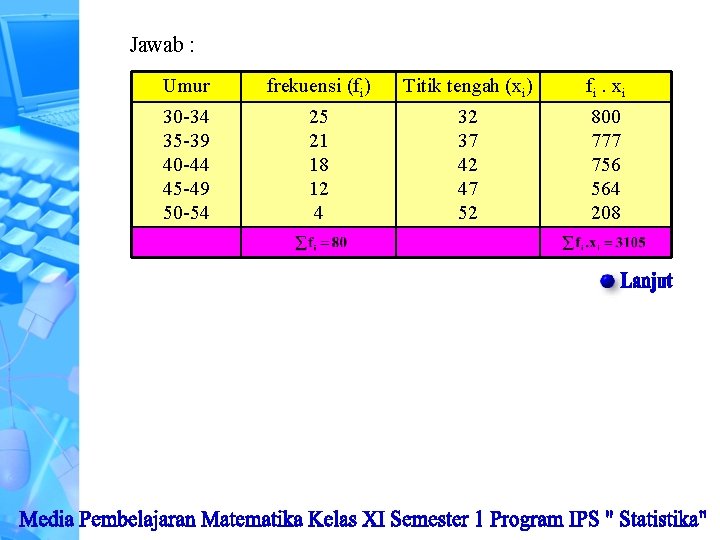
Jawab : Umur frekuensi (fi) Titik tengah (xi) fi. xi 30 -34 35 -39 40 -44 45 -49 50 -54 25 21 18 12 4 32 37 42 47 52 800 777 756 564 208

Jawab : Umur frekuensi (fi) Titik tengah (xi) fi. xi 30 -34 35 -39 40 -44 45 -49 50 -54 25 21 18 12 4 32 37 42 47 52 800 777 756 564 208 Umur rata-rata ( x= å fix i å fi )

Median (Me) umur titik tengah frekuensi f. komulatif 30 -34 35 -39 40 -44 45 -49 50 -54 29, 5 34, 5 39, 5 44, 5 49, 5 25 21 18 12 4 25 46 64 76 80 Median (Me) Kelas median terletak pada kelas 35 – 39, dan I = 5 é 12 n - (å f )2 ù Me = L 2 + ê úI f ë û 2

Modus (Mo) tepi bawah 29, 5 34, 5 39, 5 44, 5 49, 5 umur 30 -34 35 -39 40 -44 45 -49 50 -54 frekuensi 25 21 18 12 4 d 1 = 25 – 0 = 25 d 2 = 25 – 21 = 4 Kelas modus adalah kelas yang mempunyai frekuensi terbesar yaitu kelas 30 – 34, dan I = 5, maka :

Modus (Mo) tepi bawah 29, 5 34, 5 39, 5 44, 5 49, 5 umur 30 -34 35 -39 40 -44 45 -49 50 -54 frekuensi 25 21 18 12 4 d 1 = 25 – 0 = 25 d 2 = 25 – 21 = 4 Kelas modus adalah kelas yang mempunyai frekuensi terbesar yaitu kelas 30 – 34, dan I = 5, maka : æ d 1 ö ÷I Mo = L + ç è d 1 + d 2 ø

1. Carilah mean (rata-rata), median dan modus dari kumpulan data berikut ini : 6, 7, 8, 5, 6, 7, 8, 8, 9, 6, 8 2. Suatu keluarga mempunyai 6 orang anak. Anak yang bungsu berumur x tahun dan anak yang sulung berumur 3 x tahun. Empat anak yang lain berturut-turut (x+2) tahun, (x+3) tahun, (2 x-2) tahun dan (2 x+3) tahun. Jika umur rata-rata keenam naka tersebut adalah 16 tahun. Berapa umur anak sulung ? 3. Buatlah tabel distribusi frekuensi dari data tunggal nilai ujian kompetensi dasar 40 siswa : 72, 79, 88, 73, 60, 93, 71, 59, 85, 75, 66, 78, 82, 75, 93, 77, 69, 74, 68, 60 79, 62, 67, 93, 78, 86, 76, 65, 71, 75 86, 67, 73, 81, 72, 63, 76, 75, 85, 77 Tentukan nilai rata-rata (mean), median dan modusnya !

Kalau ada jarum yang patah, jangan disimpan di dalam peti. Kalau ada kata-kata saya yang salah, jangan disimpan di dalam hati. Kalau ada sumur di ladang boleh kita menumpang mandi, kalau ada umur yang panjang semoga kita berjumpa lagi