UKURAN PEMUSATAN Adalah nilai tunggal yang mewakili sekumpulan

UKURAN PEMUSATAN Adalah nilai tunggal yang mewakili sekumpulan data atau menunjukkan pusat dari nilai data

Rata – rata hitung Populasi Rumus: Rata-rata hitung populasi : Jumlah semua nilai dalam populasi Jumlah data dalam populasi Atau µ = ΣX n

Rata-rata hitung sampel Rumus: Jumlah seluruh nilai dalam sampel Jumlah data dalam sampel Atau : ẋ = Σx n

Rata-rata data berkelompok Rumus : ẋ = Σ fx n

Median Adalah suatu nilai yang berada ditengah data setelah data diurutkan Letak median dapat dicari dengan rumus: (n+1)/2 • Bila datanya ganjil maka mediannya merupakan nilai yang letaknya ditengah data setelah diurutkan • Bila datanya genap, maka nilai mediannya nilai rata dari dua data yang letaknya ditengah setelah diurutkan

Median data berkelompok 1. 2. Dengan rumus: n/2 Md = L + n/2 – c f x i f Md = Nilai Median L = Batas bawah / tepi kelas dimana median berada n = Jumlah frekuensi cf = frekuensi komulatif sebelum kelas median berada f = frekuensi dimana kelas median berada i = Besar interval kelas

Modus Adalah suatu nilai pengamatan yang paling sering muncul Cara mencari nilai modus: 1. Untuk data tidak berkelompok modus adalah nilai yang sering muncul atau frekuensi paling banyak 2. Untuk data berkelompok Mo = L + d 1 x i d 1 + d 2

Mo = Nilai modus L = Batas bawah dimana modus berada d 1 = Selisih frekuensi kelas modus dengan batas sebelumnya d 2 = Selisih frekuensi kelas modus dengan batas sesudahnya i = Besar interval kelas

Contoh: 1 ( Rata-rata hitung populasi dan sampel) Bank Nilai kredit (Rp trilliun) Danamon 41 BRI 90 BCA 61 Mandiri 137 BNI 66 Nilai µ = 41 + 90 + 61 + 137 + 66 5 = 395 / 5 = 79

Contoh 2: Berikut adalah data yang sudah dikelompokkan dari 20 saham perusahaan Interval Nilai Tengah Jumlah frekuensi 160 - 303 231, 5 2 304 – 447 375, 5 5 448 – 591 519, 5 9 592 – 735 663, 5 3 736 - 879 807, 5 1

. ẋ = Σ fx n = (2 x 231, 5) + (5 x 375, 5) + (9 x 519, 5) + (3 x (1 x 807, 5) = 9814 / 20 = 490, 7 20 663, 5) +

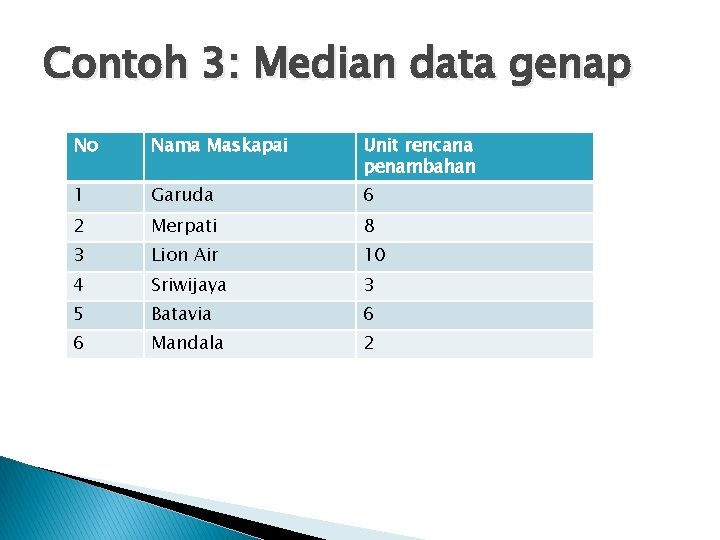
Contoh 3: Median data genap No Nama Maskapai Unit rencana penambahan 1 Garuda 6 2 Merpati 8 3 Lion Air 10 4 Sriwijaya 3 5 Batavia 6 6 Mandala 2

� Median =(n+1)/2 =(6+1)/2 = 3, 5 Urutan data dari terkecil ke terbesar 2 3 6 6 8 10 Maka mediannya = 6 + 6 = 6 2

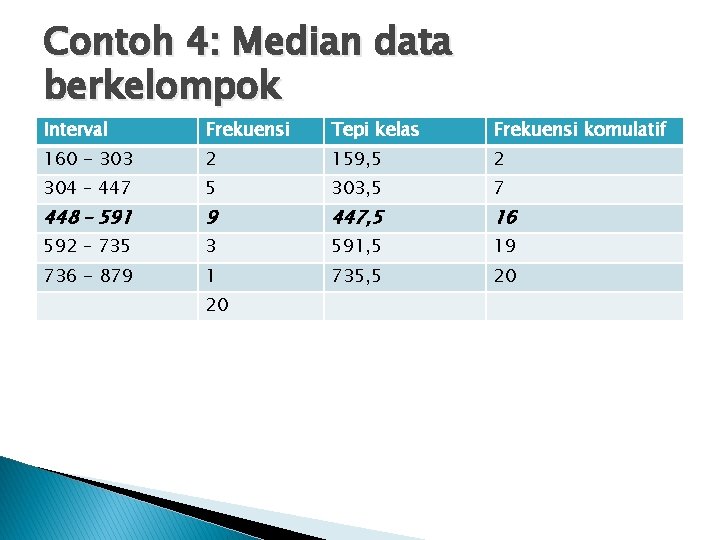
Contoh 4: Median data berkelompok Interval Frekuensi Tepi kelas Frekuensi komulatif 160 - 303 2 159, 5 2 304 – 447 5 303, 5 7 448 – 591 9 447, 5 16 592 – 735 3 591, 5 19 736 - 879 1 735, 5 20 20

1. 2. Rumus: n/2 = 20 / 2 = 10 Md = L + n/2 – cf x i f = 447, 5 + 20/2 – 7 x 143 9 = 447, 5 + 3/9 x 143 = 495, 17

Contoh 5: Modus data berkelompok Pada contoh 4 frekuensi yang paling banyak muncul adalah 9, maka Mo = L + d 1 xi d 1 + d 2 = 447, 5 + ( 9 -5) x 143 (9 -5) + (9 -3) = 447, 5 + 4 x 143 (4 + 6) = 504, 7