UJI HIPOTESIS Uji Ratarata Proporsi dan Simpangan Baku

UJI HIPOTESIS Uji Rata-rata, Proporsi dan Simpangan Baku

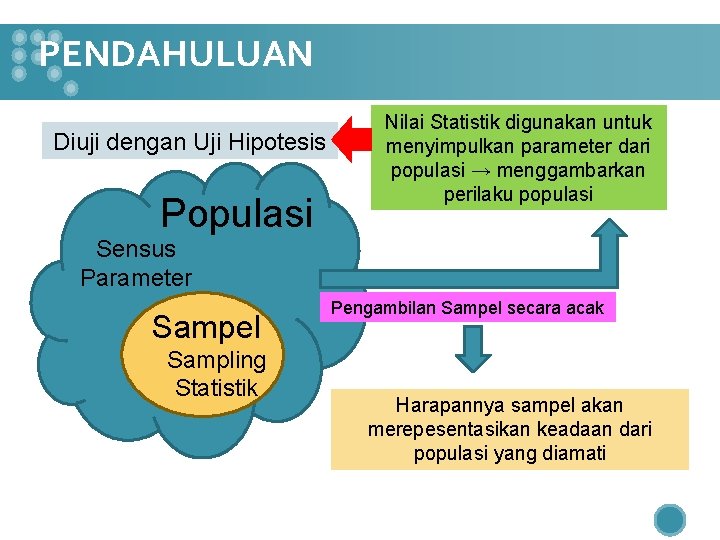
PENDAHULUAN Diuji dengan Uji Hipotesis Populasi Nilai Statistik digunakan untuk menyimpulkan parameter dari populasi → menggambarkan perilaku populasi Sensus Parameter Sampel Sampling Statistik Pengambilan Sampel secara acak Harapannya sampel akan merepesentasikan keadaan dari populasi yang diamati

ISTILAH • Hipotesis : asumsi atau dugaan mengenai sesuatu hal yang dibuat untuk menjelaskan suatu hal. • Asumsi atau dugaan mengenai populasi, (Nilai-nilai parameter populasi) Hipotesis statistik. • Kekeliruan tipe I : menolak hipotesis yang benar. • Kekeliruan tipe I biasa dinyatakan dengan α • Kekeliruan tipe II : menerima hipotesis yang salah • Kekeliruan tipe II biasa dinyatakan dengan β

ISTILAH • α = taraf signifikansi atau taraf arti atau taraf nyata. • α yang biasa digunakan 0. 05 atau 0. 01 • α = 0. 05 artinya kira-kira 5 dari setiap 100 kesimpulan kita telah melakukan kesalahan tipe I yaitu menolak hipotesis yang seharusnya diterima. • Atau dengan kata lain kira-kira 95% yakin bahwa kita telah membuat kesimpulan yang benar

LANGKAH – LANGKAH UJI HIPOTESIS • 1. PERUMUSAN HIPOTESIS – Perumusan hipotesis dilakukan dengan dua macam, yaitu hipotesis awal, , dan hipotesis alternatif, . – Pengujian hipotesis uji satu pihak – Pengujian hipotesis uji 2 pihak

Tentukan Ho dan H 1 • Seorang manager penjual mobil ingin menerapkan aturan bonus baru untuk meningkatkan penjualan mobil. Saat ini rata-rata penjualan mobil per bulan adalah 14 mobil. Untuk mengetahui keefektifan dari penerapan aturan tersebut maka setelah 1 bulan aturan diterapkan diambil data penjualan dari 15 orang sales. Tentukan Ho dan H 1 yang tepat untuk pengujian hipotesisnya 6

Tentukan Ho dan H 1 • Sebuah perusahaan memproduksi karton pembungkus detergen yang menampung detergen dengan berat 1. 5 kg. Perusahaan ingin mengetahui apakah ukuran pembungkus detergen yang diproduksi masih memiliki ukuran yang sesuai dengan berat detergen yang akan diisi. Apabila ukuran karton berubah maka proses produksi akan dihentikan dilakukan penyesuaian kembali. Tentukan Ho dan H 1 untuk mengujian hipotesis dari kasus diatas 7

LANGKAH – LANGKAH UJI HIPOTESIS • 2. Menentukan distribusi yang akan digunakan, apakah z, t, , F atau yang lain. • 3. Penentuan kriteria uji atau penentuan daerah kritis • 4. Pilih taraf signifikansi atau taraf nyata α • 5. Hitung nilai statistik yang dibutuhkan • 6. Buat kesimpulan

UJI RATA-RATA µ : UJI 2 PIHAK • 1. Jika varians atau simpangan baku populasi diketahui – Pasangan hipotesisnya – Gunakan pendekatan distribusi normal, sehingga – Kriteria Uji : – Terima jika – Tolak untuk nilai lainnya

UJI RATA-RATA µ : UJI 2 PIHAK • 2. Jika varians atau simpangan baku populasi tidak diketahui – Pasangan hipotesis – Statistik uji mengunakan – Kriteria uji : – Terima jika – Tolak untuk nilai lainnya

Contoh Soal • Sebuah perusahaan olah raga mengembangkan jenis batang pancing mengklaim rata-rata kekuatan pancingnya 8 kg. Untuk mengecek kebenaran tersebut diambil 25 sampel batang pancing dan diperoleh rata-rata dari kekuatan pancing adalah 7, 8 kg dan simpangan baku 0, 3. Dengan menggunakan tarafnya 0, 01 tentukan apakah rata-rata kekuatan pancing tersebut masih 8 kg atau tidak? 11

CONTOH SOAL • Pengusaha lampu pijar A mengatakan bahwa lampunya bisa tahan pakai sekitar 800 jam. Akhir-akhir ini timbul dugaan bahwa masa pakai lampu itu telah berubah. Untuk menentukan hal ini, dilakukan penelitian dengan jalan menguji 50 lampu. Ternyata rata-rata nya 792 jam. Jika diketahui berdasarkan pengalaman bahwa simpangan baku populasi nya 60 jam, selidikilah dengan taraf nyata 0, 05 apakah kualitas lampu itu sudah berubah atau belum?

UJI RATA-RATA µ : UJI 1 PIHAK • Pasangan hipotesis • 1. jika σ diketahui: – Statistik Uji menggunakan – Kriteria uji Terima dalam hal lainnya jika ditolak

UJI RATA-RATA µ : UJI 1 PIHAK • Jika σ tidak diketahui – Statistik uji yang digunakan – Kriteria Uji : • Terima jika

CONTOH SOAL • Waktu yang diperlukan permahasiswa untuk mendaftarkan diri di suatu universitas adalah 50 menit. Suatu prosedur pendaftaran baru yang menggunakan mesin modern sedang dicoba. Bila dari sampel acak sebanyak 12 mahasiswa memerlukan rata-rata pendaftaran 42 menit dengan simpangan baku 11, 9 menit. Dengan menggunakan sistem baru tersebut, ujilah hipotesis bahwa rata-rata populasi sekarang kurang dari 50 menit. • A. gunakan taraf nyata 5% • B. gunakan taraf nyata 1%

CONTOH SOAL • Dari 100 sampel acak diketahui bahwa rata-rata usia kematian pada penduduk Amerika tahun lalu adalah 71, 8 tahun dengan simpangan baku 8, 9 tahun. Dengan taraf nyata 0. 05, apakah hasil ini cukup untuk menunjukkan bahwa harapan hidup umur sekarang lebih dari 70 tahun ? 16

UJI PROPORSI • 1. UJI PROPORSI DUA PIHAK • Rumusan Hipotesis : • Statistik Uji : • Kriteria Uji : Dengan taraf nyata sebesar α, terima jika

UJI PROPORSI • 2. UJI PROPORSI SATU PIHAK • Rumusan Hipotesis atau • Statistik Uji • Kriteria Uji dengan taraf nyata sebesar α, • Untuk : Terima jika

CONTOH SOAL • Suatu obat penenang ketegangan syaraf diduga hanya 60% efektif. Hasil percobaan dengan obat baru terhadap 100 orang dewasa penderita ketegangan syaraf diambil secara acak, menunjukkan bahwa obat baru itu 70% efektif. Apakah ini merupakan bukti yang cukup untuk menyimpulkan bahwa obat baru itu lebih baik daripada yang beredar sekarang? Gunakan taraf nyata 5% • Seorang pejabat mengatakan bahwa paling banyak 60% anggota masyarakat termasuk golongan A. sebuah sampel acak telah diambil yang terdiri atas 8500 orang, dan ternyata 5426 diantaranya termasuk golongan A. apabila α = 0. 01 benarkah pernyataan tersebut diatas.

CONTOH SOAL • Penghasil obat alergi menyatakan bahwa obatnya 90% efektif untuk dapat menyembuhkan penderita dalam tempo 8 jam. Hasil pengobatan dengan obat itu terhadap 160 pasien penderita alergi ternyata 137 sembuh dalam tempo 8 jam. Dengan taraf nyata 5%, tentukan apakah pernyataan pengusaha tersebut dapat diterima atau tidak.

UJI VARIANS • 1. UJI VARIANS DUA PIHAK • Rumusan Hipotesis • Statistik Uji : • Kriteria uji dengan taraf nyata sebesar α Terima jika

UJI VARIANS 2. UJI VARIANS SATU PIHAK • Rumusan Hipotesis atau • Statistik Uji • Kriteria Uji denga taraf nyata sebesar α Untuk . Terima jika

CONTOH SOAL • Dalam suatu sampel acak 8 buah batang rokok menghasilkan simpangan baku kadar nikotin sebanyak 1, 8 mg. dengan taraf nyata dapatkah disimpulkan bahwa simpangan baku sesungguhnya 1, 3 mg dengan α=1%

Contoh Soal • Sebuah perusahaan aki mobil mengatakan bahwa umur aki yang diproduksi mempunyai simpangan baku lebih dari 0, 9 tahun. Jika diambil sampel acak berukuran 10 diperoleh simpangan baku umur aki adalah 1, 2 tahun. Dengan menggunakan taraf nyata 0, 05 apa yang dapat disimpulkan? 24