Uji Hipotesis Chi Square 2 1 Uji Statistik

Uji Hipotesis Chi Square 2 (χ ) 1

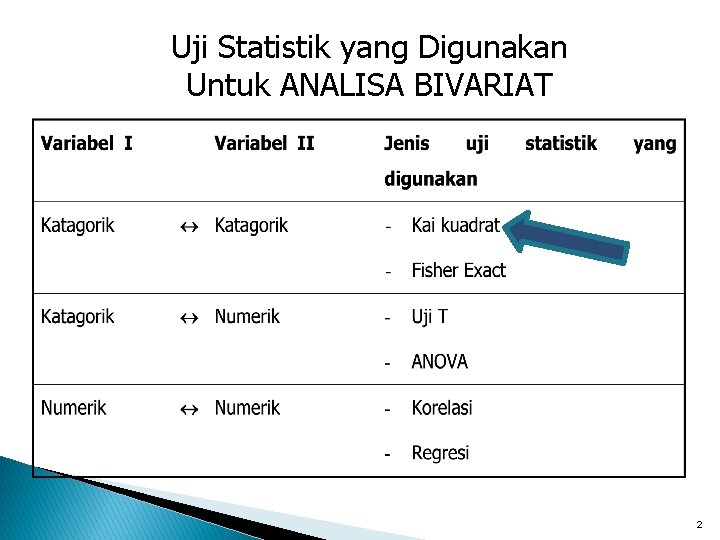
Uji Statistik yang Digunakan Untuk ANALISA BIVARIAT 2

Contoh Apakah ada perbedaan proporsi hipertensi pada populasi perokok dan populasi bukan perokok Apakah ada perbedaan proporsi anemia pada ibu dengan sosek ekonomi tinggi, sedang, dan rendah Disusun dalam suatu tabel (tabel kontingensi) 3

TUJUAN UJI CHI SQUARE �Secara spesifik uji chi square dapat digunakan untuk menentukan/menguji: ◦ Ada tidaknya hubungan/asosiasi antara 2 variabel (test of independency) ◦ Apakah suatu kelompok homogen dengan sub kelompok lain (test of homogenity) ◦ Apakah ada kesesuaian antara pengamatan dengan parameter tertentu yang dispesifikasikan (Goodness of fit) 4

PERSYARATAN/ASUMSI Jenis data kategori Sampel independen Distribusi tidak normal/tidak diketahui distribusinya (free distribution) 5

PRINSIP DASAR UJI CHI SQUARE � Membandingkan frekuensi yang terjadi (observasi) dengan frekuensi harapan (ekspektasi) � Pembuktian dengan uji chi square menggunakan formula: Pearson Chi Square: χ2 = dengan df = (b-1)(k-1) fo= nilai observasi (pengamatan) fe = nilai ekspektasi (harapan) b = jumlah baris k = jumlah kolom 6

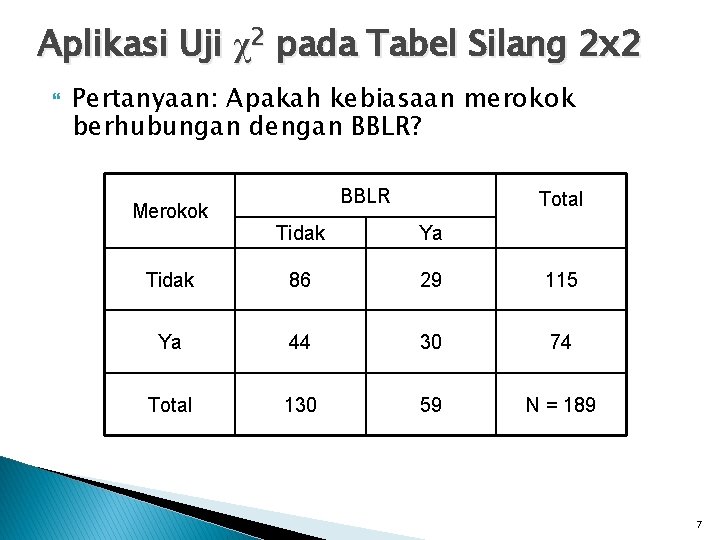
Aplikasi Uji χ2 pada Tabel Silang 2 x 2 Pertanyaan: Apakah kebiasaan merokok berhubungan dengan BBLR? Merokok BBLR Total Tidak Ya Tidak 86 29 115 Ya 44 30 74 Total 130 59 N = 189 7

Langkah 1 Menentukan hipotesis statistik Hipotesis nol (Ho): ◦ Proporsi BBLR pada ibu perokok sama dengan proporsi BBLR pada ibu yang bukan perokok ◦ ATAU tidak ada hubungan merokok dengan kejadian BBLR Hipotesis alternatif (Ha): ◦ Proporsi BBLR pada ibu perokok berbeda proporsi BBLR pada ibu yang bukan perokok ◦ ATAU ada hubungan merokok dengan kejadian BBLR 8

Langkah 3 Perhitungan Uji Statistik � Formula: χ2 = Metode: 1. 2. Hitung nilai/frekuensi ekspektasi dari masing sel. Lengkapi tabel perhitungan untuk memperoleh χ2 (hitung) 9

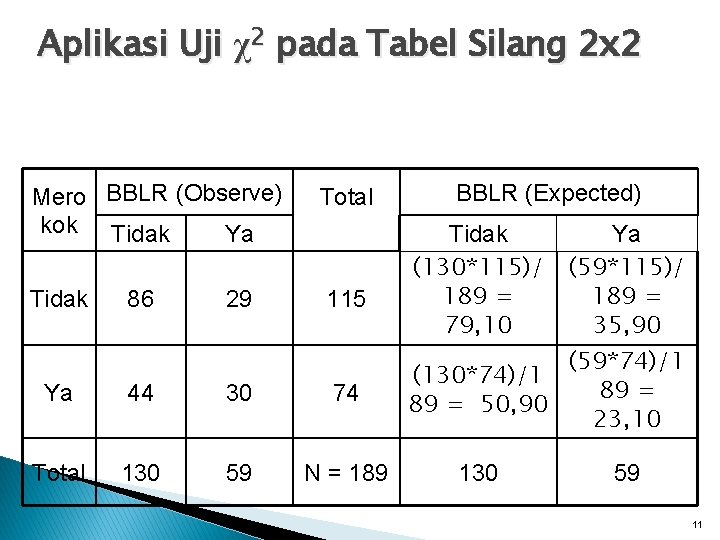
Menghitung nilai/frekuensi ekspektasi masing-masing sel E= Perkalian antara marginal kolom dan marginal baris masing-masing sel dan dibagi N. (130*115)/189 = 79, 10 (59*115)/189 = 35, 90 (130*74)/189 = 50, 90 (59*74)/189 = 23, 10 10

Aplikasi Uji χ2 pada Tabel Silang 2 x 2 Mero BBLR (Observe) kok Tidak Ya Total Tidak 115 86 29 BBLR (Expected) Tidak (130*115)/ 189 = 79, 10 Ya 44 30 74 (130*74)/1 89 = 50, 90 Total 130 59 N = 189 130 Ya (59*115)/ 189 = 35, 90 (59*74)/1 89 = 23, 10 59 11

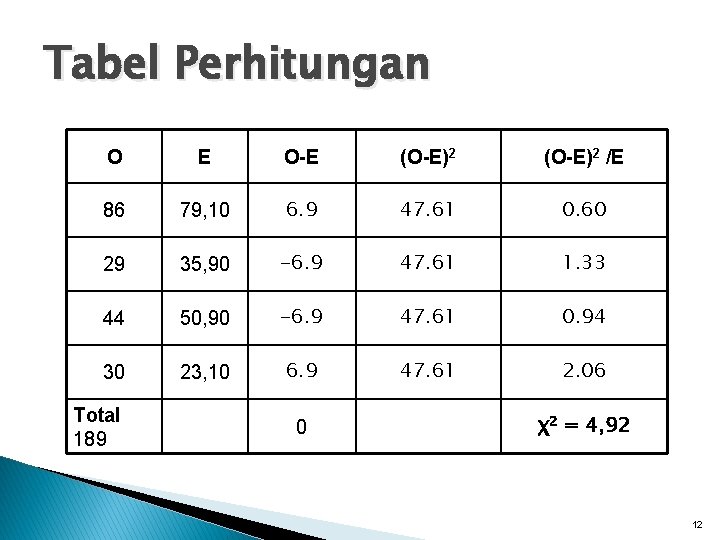
Tabel Perhitungan O E O-E (O-E)2 /E 86 79, 10 6. 9 47. 61 0. 60 29 35, 90 -6. 9 47. 61 1. 33 44 50, 90 -6. 9 47. 61 0. 94 30 23, 10 6. 9 47. 61 2. 06 Total 189 0 χ2 = 4, 92 12

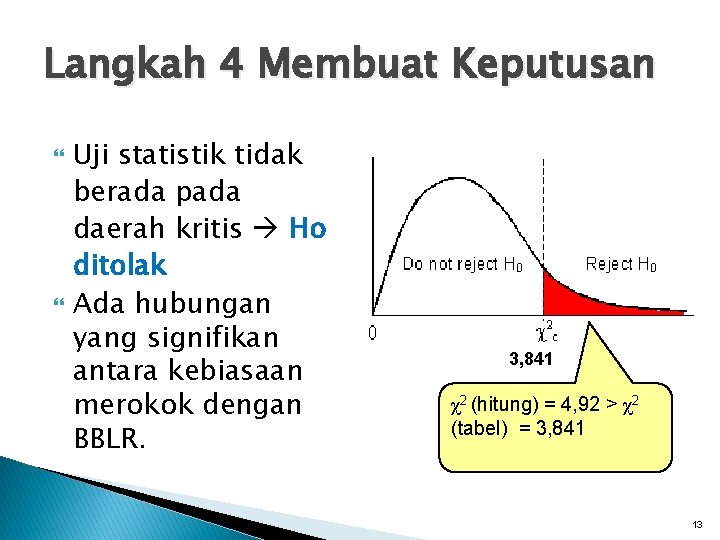
Langkah 4 Membuat Keputusan Uji statistik tidak berada pada daerah kritis Ho ditolak Ada hubungan yang signifikan antara kebiasaan merokok dengan BBLR. 3, 841 χ2 (hitung) = 4, 92 > χ2 (tabel) = 3, 841 13

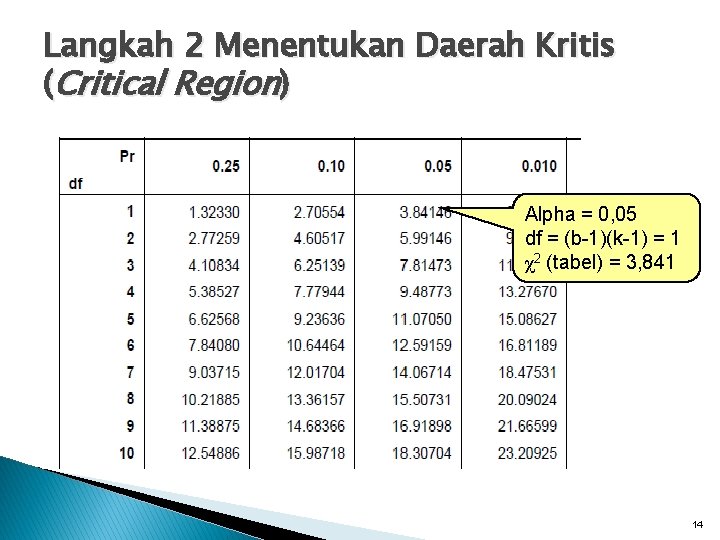
Langkah 2 Menentukan Daerah Kritis (Critical Region) Alpha = 0, 05 df = (b-1)(k-1) = 1 χ2 (tabel) = 3, 841 14

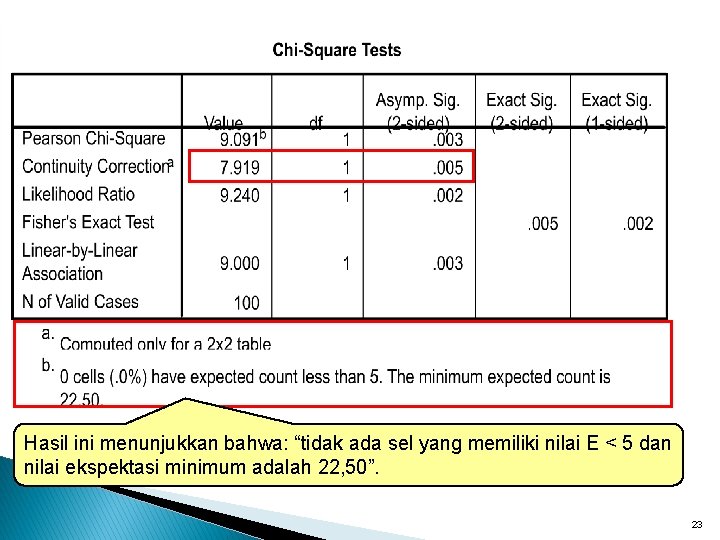
Persyaratan Penggunaan Chi Square � Pearson Chi Square/Likehood Untuk tabel > 2 x 2 (misal 3 x 2 atau 3 x 3) dengan memperhatikan persyaratan: ◦ Tidak ada frekuensi harapan kurang dari 1 (E<1) ◦ Nilai frekuensi harapan < 5 maksimal 20% ◦ Apabila kedua persyaratan di atas tidak dipenuhi, maka penggabungan kategori perlu dilakukan agar diperoleh nilai harapan yang berharga besar � Yates Correction: Untuk tabel 2 x 2 bila tidak ada nilai E < 5, maka dipakai Continuity Correction � Fisher Exact Test Untuk tabel 2 x 2 bila terdapat nilai E < 5 maka digunakan Uji Fisher Exact 15

Aplikasi Uji Chi Square (Tabel 2 x 2) Menggunakan Spss 16 Kasus Suatu penelitian ingin mengetahui hubungan antara perilaku merokok (merokok dan tidak merokok) dengan status fertilitas seorang pria (subur dan tidak subur).

17

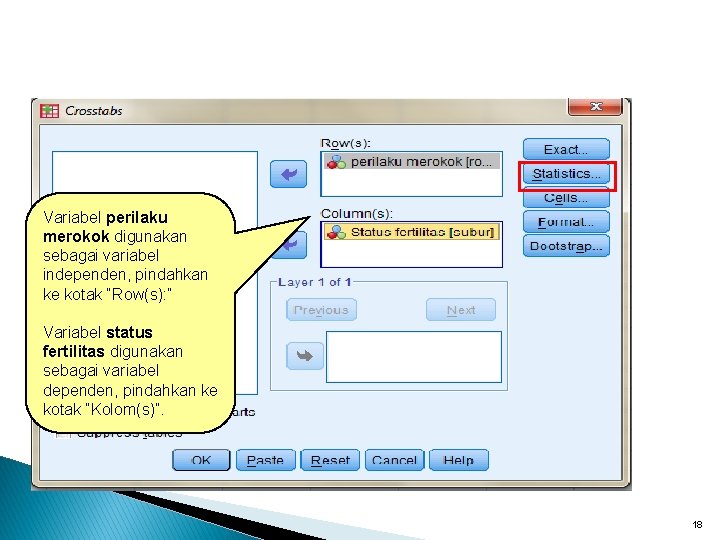
Variabel perilaku merokok digunakan sebagai variabel independen, pindahkan ke kotak “Row(s): ” Variabel status fertilitas digunakan sebagai variabel dependen, pindahkan ke kotak “Kolom(s)”. 18

19

20

21

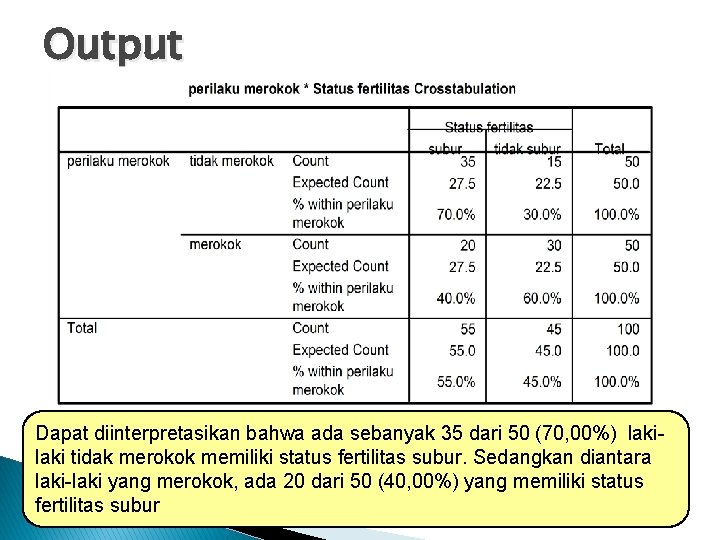
Output Dapat diinterpretasikan bahwa ada sebanyak 35 dari 50 (70, 00%) laki tidak merokok memiliki status fertilitas subur. Sedangkan diantara laki-laki yang merokok, ada 20 dari 50 (40, 00%) yang memiliki status fertilitas subur 22

Hasil ini menunjukkan bahwa: “tidak ada sel yang memiliki nilai E < 5 dan nilai ekspektasi minimum adalah 22, 50”. 23

Keterbatasan Uji Chi Square Uji chi quare hanya membuktikan bahwa ada hubungan (P-value) Tidak menggambarkan kekuatan hubungan. Untuk menggambarkan hubungan digunakan ukuran OR dan RR 24

Kekuatan Hubungan RR (Relative Risk) = OR (Odds Ratio) = A/(A+B) ----C/(C+D) AD / BC 25

Langkah Menentukan OR dan RR Menggunakan SPSS 26

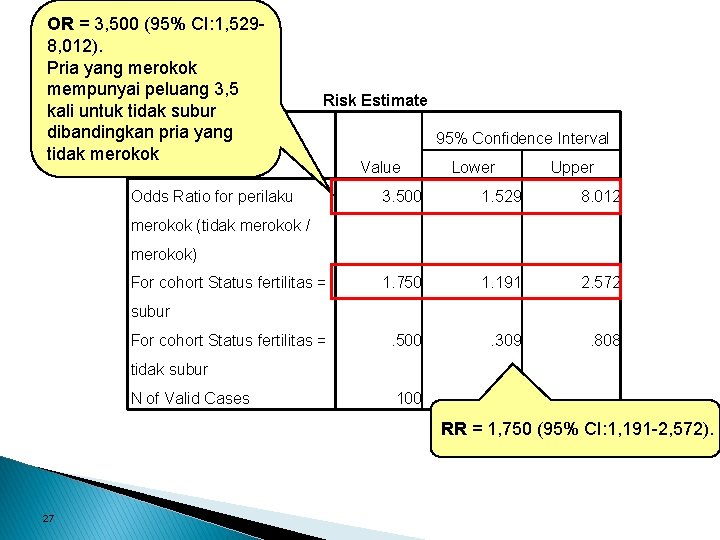
OR = 3, 500 (95% CI: 1, 5298, 012). Pria yang merokok mempunyai peluang 3, 5 kali untuk tidak subur dibandingkan pria yang tidak merokok Output Risk Estimate Odds Ratio for perilaku 95% Confidence Interval Value Lower Upper 3. 500 1. 529 8. 012 1. 750 1. 191 2. 572 . 500 . 309 . 808 merokok (tidak merokok / merokok) For cohort Status fertilitas = subur For cohort Status fertilitas = tidak subur N of Valid Cases 100 RR = 1, 750 (95% CI: 1, 191 -2, 572). 27

Aplikasi Uji Chi Square pada Tabel > 2 x 2 Contoh: Ingin diketahui apakah ada hubungan antara tingkat pendidikan ibu dengan pemanfaatan pelayanan ANC 28

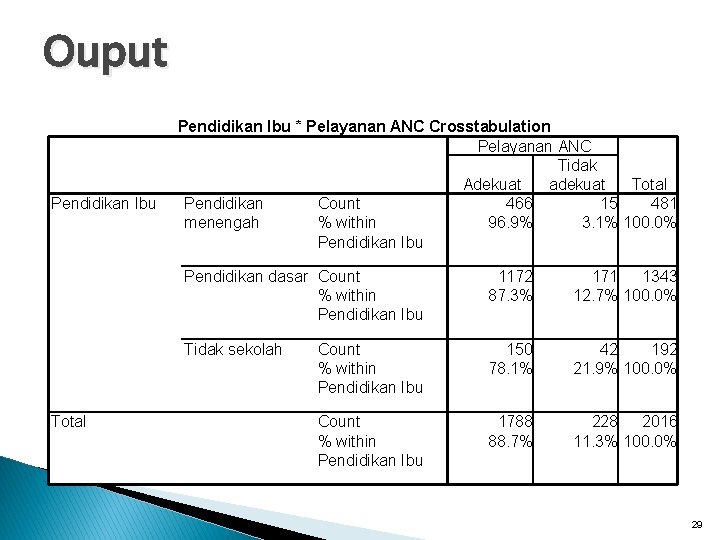
Ouput Pendidikan Ibu Total Pendidikan Ibu * Pelayanan ANC Crosstabulation Pelayanan ANC Tidak Adekuat adekuat Total Pendidikan Count 466 15 481 % within 96. 9% 3. 1% 100. 0% menengah Pendidikan Ibu Pendidikan dasar Count % within Pendidikan Ibu 1172 87. 3% 171 1343 12. 7% 100. 0% Tidak sekolah Count % within Pendidikan Ibu 150 78. 1% 42 192 21. 9% 100. 0% Count % within Pendidikan Ibu 1788 88. 7% 228 2016 11. 3% 100. 0% 29

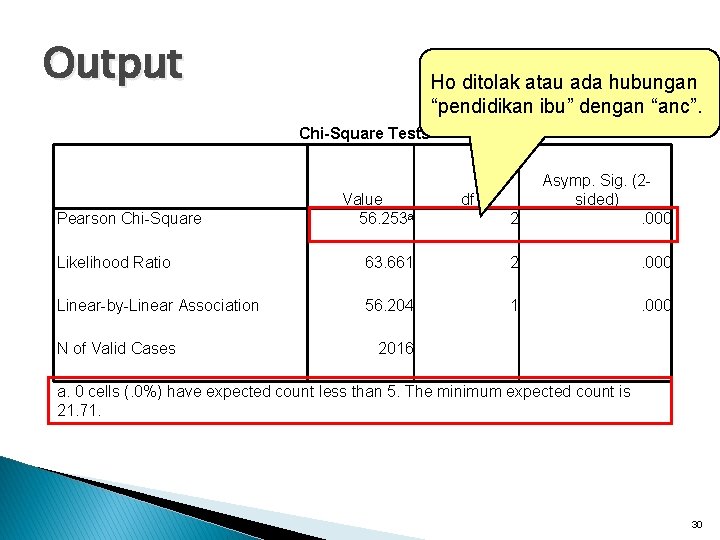
Output Ho ditolak atau ada hubungan “pendidikan ibu” dengan “anc”. Chi-Square Tests Pearson Chi-Square Value 56. 253 a 2 Asymp. Sig. (2 sided). 000 df Likelihood Ratio 63. 661 2 . 000 Linear-by-Linear Association 56. 204 1 . 000 N of Valid Cases 2016 a. 0 cells (. 0%) have expected count less than 5. The minimum expected count is 21. 71. 30

Dummy Variabel Pada tabel > 2 x 2, tidak bisa ditampilkan nilai OR Tiga cara: ◦ Harus dibuat dummy variabel tabel dahulu, kemudian dilakukan Crosstabs ◦ Lakukan analisis regresi logistik sederhana 31

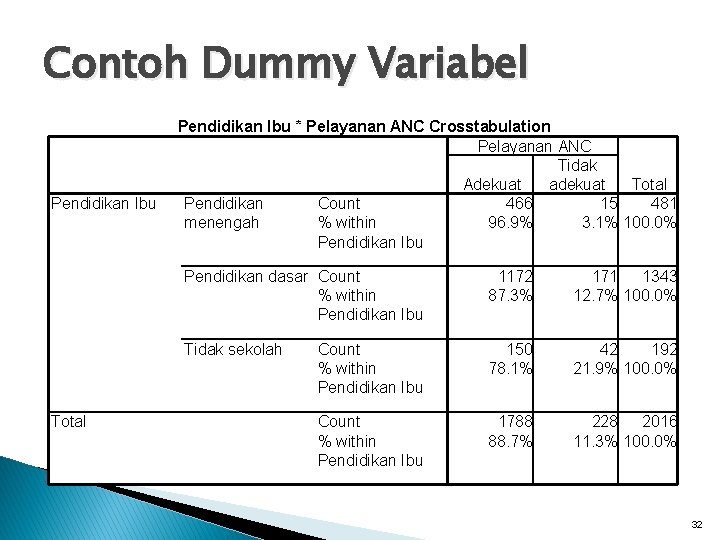
Contoh Dummy Variabel Pendidikan Ibu Total Pendidikan Ibu * Pelayanan ANC Crosstabulation Pelayanan ANC Tidak Adekuat adekuat Total Pendidikan Count 466 15 481 % within 96. 9% 3. 1% 100. 0% menengah Pendidikan Ibu Pendidikan dasar Count % within Pendidikan Ibu 1172 87. 3% 171 1343 12. 7% 100. 0% Tidak sekolah Count % within Pendidikan Ibu 150 78. 1% 42 192 21. 9% 100. 0% Count % within Pendidikan Ibu 1788 88. 7% 228 2016 11. 3% 100. 0% 32

Untuk membuat dummy variabel dari pendidikan (0. Pendidikan menengah, 1. Pendidikan dasar & 2. Tidak sekolah), ditetapkan kelompok mana yang akan dijadikan sebagai pembanding Sebagai kelompok pembanding kita tetapkan Tidak sekolah. Melakukan transformasi data dengan menu RECODE: ◦ Pendidikan_1 (0=Tidak sekolah, 1=Pendidikan menengah) ◦ Pendidikan_2 (0=Tidak sekolah, 1=Pendidikan dasar) 33

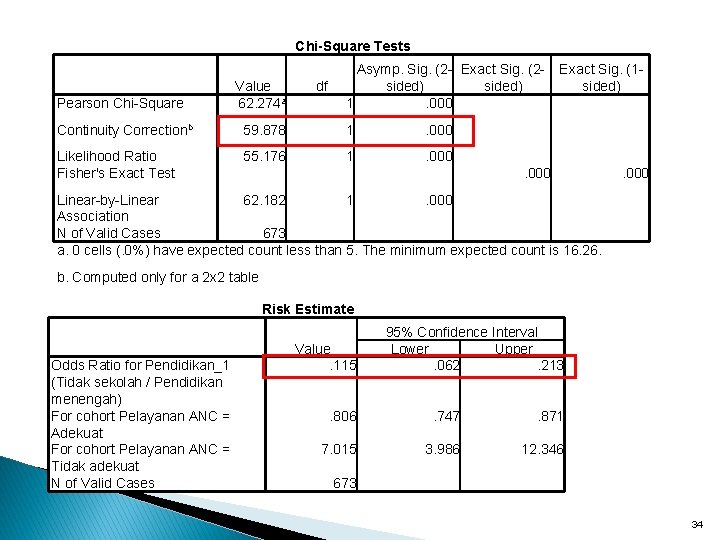
Chi-Square Tests Pearson Chi-Square Value 62. 274 a df Asymp. Sig. (2 - Exact Sig. (2 sided) 1. 000 Continuity Correctionb 59. 878 1 . 000 Likelihood Ratio Fisher's Exact Test 55. 176 1 . 000 Exact Sig. (1 sided) . 000 Linear-by-Linear 62. 182 1. 000 Association N of Valid Cases 673 a. 0 cells (. 0%) have expected count less than 5. The minimum expected count is 16. 26. b. Computed only for a 2 x 2 table Risk Estimate Odds Ratio for Pendidikan_1 (Tidak sekolah / Pendidikan menengah) For cohort Pelayanan ANC = Adekuat For cohort Pelayanan ANC = Tidak adekuat N of Valid Cases Value. 115 95% Confidence Interval Lower Upper. 062. 213 . 806 . 747 . 871 7. 015 3. 986 12. 346 673 34

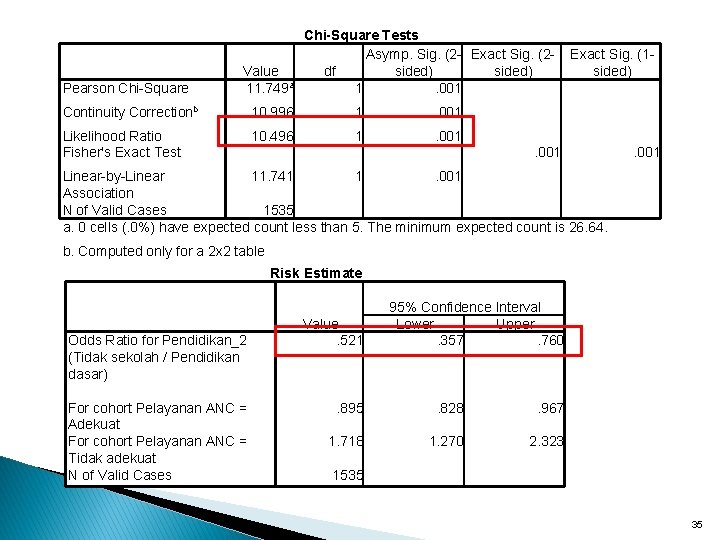
Pearson Chi-Square Value 11. 749 a Chi-Square Tests Asymp. Sig. (2 - Exact Sig. (2 df sided) 1. 001 Continuity Correctionb 10. 996 1 . 001 Likelihood Ratio Fisher's Exact Test 10. 496 1 . 001 Exact Sig. (1 sided) . 001 Linear-by-Linear 11. 741 1. 001 Association N of Valid Cases 1535 a. 0 cells (. 0%) have expected count less than 5. The minimum expected count is 26. 64. b. Computed only for a 2 x 2 table Risk Estimate Odds Ratio for Pendidikan_2 (Tidak sekolah / Pendidikan dasar) For cohort Pelayanan ANC = Adekuat For cohort Pelayanan ANC = Tidak adekuat N of Valid Cases Value. 521 95% Confidence Interval Lower Upper. 357. 760 . 895 . 828 . 967 1. 718 1. 270 2. 323 1535 35

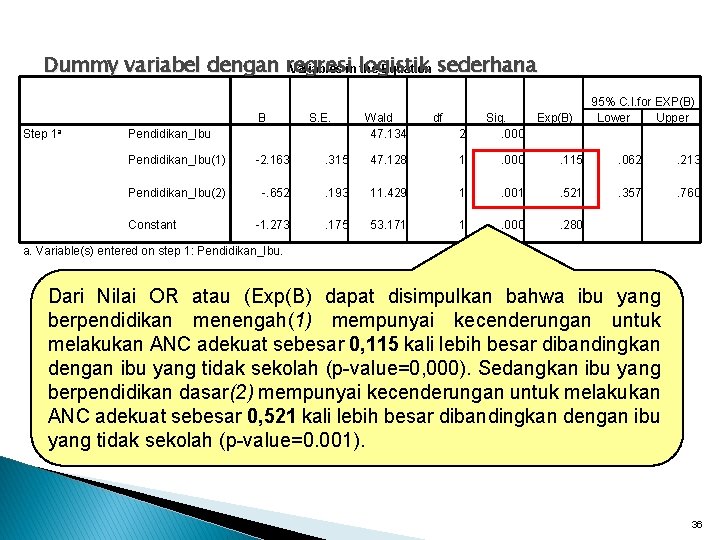
Dummy variabel dengan regresi Variables in logistik the Equation sederhana B Step 1 a S. E. Pendidikan_Ibu Wald 47. 134 df 2 Sig. . 000 Exp(B) 95% C. I. for EXP(B) Lower Upper Pendidikan_Ibu(1) -2. 163 . 315 47. 128 1 . 000 . 115 . 062 . 213 Pendidikan_Ibu(2) -. 652 . 193 11. 429 1 . 001 . 521 . 357 . 760 -1. 273 . 175 53. 171 1 . 000 . 280 Constant a. Variable(s) entered on step 1: Pendidikan_Ibu. Dari Nilai OR atau (Exp(B) dapat disimpulkan bahwa ibu yang berpendidikan menengah(1) mempunyai kecenderungan untuk melakukan ANC adekuat sebesar 0, 115 kali lebih besar dibandingkan dengan ibu yang tidak sekolah (p-value=0, 000). Sedangkan ibu yang berpendidikan dasar(2) mempunyai kecenderungan untuk melakukan ANC adekuat sebesar 0, 521 kali lebih besar dibandingkan dengan ibu yang tidak sekolah (p-value=0. 001). 36

Referensi n n Jan W. Kuzma, 1984, Basic Statistics for the Health Sciences, California: Meyfield Publishing Company. Pagano, M. , & Gauvreau, K. , 1993. Principles of Biostatistics. California: Wadsworth Publishing Company. Hastono, S. P. , 2001. Modul Analisis Data. FKM UI. Dahlan, Sopiyudin. 2008. Statistik untuk Kedokteran dan Kesehatan. Seri Evidence Based Medicine 2 Edisi 3. Jakarta: Penerbit Salemba Medika. 37