Uji Hipotesis Bagian dua DUA TIPE HIPOTESIS HIPOTESIS

Uji Hipotesis Bagian dua

DUA TIPE HIPOTESIS • HIPOTESIS NOL (H 0) YAITU HIPOTESIS YANG MENYATAKAN TIDAK ADANYA HUBUNGAN ANTARA DUA VARIABEL / LEBIH ATAU TIDAK ADANYA PERBEDAAN ANTARA DUA KELOMPOK / LEBIH • HIPOTESIS ALTERNATIF (H 1) YAITU HIPOTESIS YANG MENYATAKAN ADANYA HUBUNGAN ANTARA DUA VARIABEL/LEBIH ATAU ADANYA PERBEDAAN ANTARA DUA KELOMPOK / LEBIH

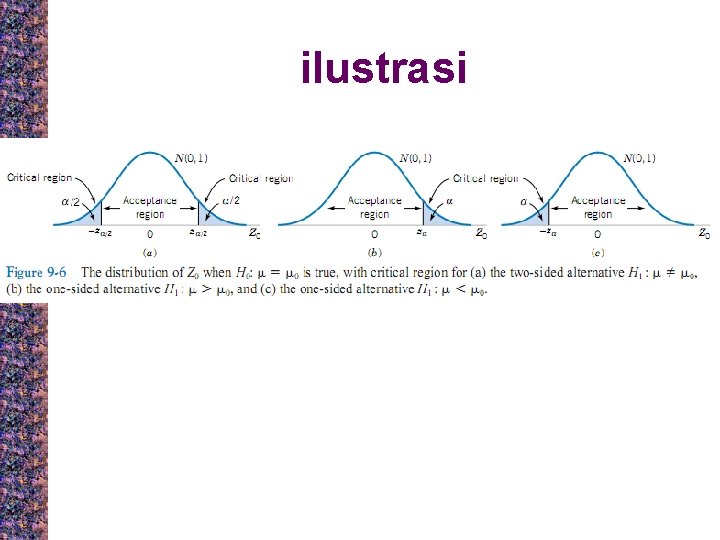
Uji hipotesis rata-rata, variansi diketahui Hipotesis : Uji statistika :

ilustrasi

Langkah-langkah uji hipotesis i. Hipotesis : ii. Tingkat Signifikansi

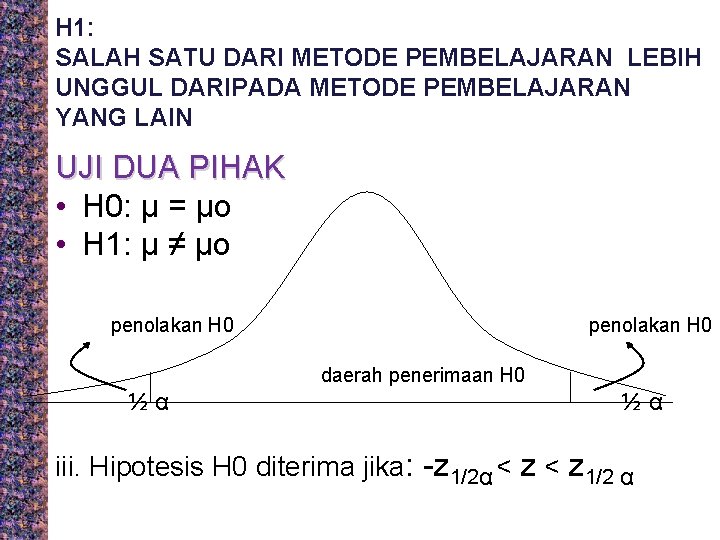
H 1: SALAH SATU DARI METODE PEMBELAJARAN LEBIH UNGGUL DARIPADA METODE PEMBELAJARAN YANG LAIN UJI DUA PIHAK • H 0: μ = μo • H 1: μ ≠ μo penolakan H 0 daerah penerimaan H 0 ½α ½α iii. Hipotesis H 0 diterima jika: -z 1/2α < z 1/2 α

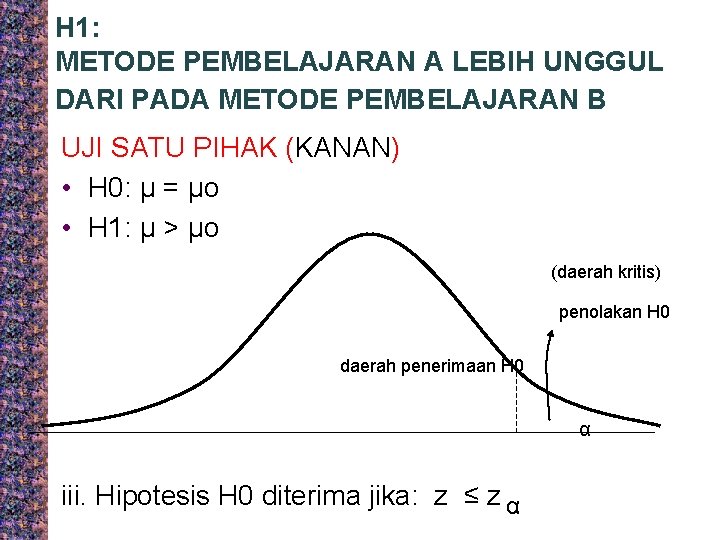
H 1: METODE PEMBELAJARAN A LEBIH UNGGUL DARI PADA METODE PEMBELAJARAN B UJI SATU PIHAK (KANAN) • H 0: μ = μo • H 1: μ > μo (daerah kritis) penolakan H 0 daerah penerimaan H 0 α iii. Hipotesis H 0 diterima jika: z ≤ z α

H 1: DENGAN SISTEM INJEKSI PENGGUNAAN BAHAN BAKAR LEBIH IRIT DARIPADA SISTEM BIASA UJI SATU PIHAK (KIRI) • H 0: μ = μo • H 1: μ < μo (daerah kritis) penolakan H 0 daerah penerimaan H 0 α iii. Hipotesis H 0 diterima jika: z ≥ -zα

iv. Hitungan :

Contoh Akan diuji bahwa rata-rata tinggi mahasiswa PKIMIA adalah 160 cm atau berbeda dari itu. Jika tingkat signifikansi 5% dan diambil sampel random 100 orang mahasiswa ternyata rata-rata 163. 5 cm dengan deviasi standar 4. 8 cm. Apakah hipotesis di atas benar?

Penyelesaian i. Hipotesis : ii. Tingkat signifikansi 0. 05 iii. H 0 diterima jika

iv. Hitungan v. Karena Z=7. 29>1. 96 maka H 0 ditolak Jadi diterima dkl rata-rata TB mahasiswa PKIMIA berbeda dari 160 cm

Uji Hipotesis rata-rata berdistribusi Normal, variansi tidak kdiketahui

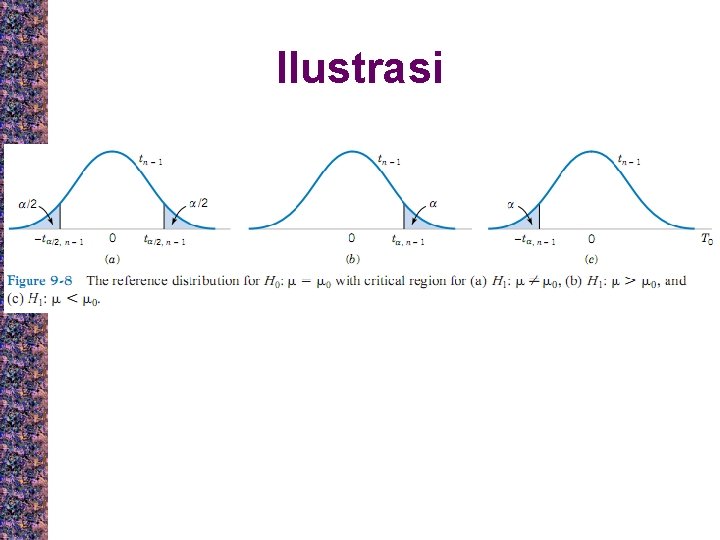
Ilustrasi

contoh Rata-rata sampel 0. 83725 dan standar deviasi =0. 02456

uji hipotesis PROPORSI i. Hipotesis : ii. Tingkat Signifikansi iii. Daerah kritik idem dengan atas

iv. Hitungan :

Contoh 2 Seorang apoteker menyatakan bahwa obat penenang buatannya manjur 90%. Ternyata dalam sampel 200 orang, obat tersebut hanya manjur untuk 160 orang. Apakah pernyataan apoteker tsb benar?

Penyelesaian i. Hipotesis : ii. Tingkat signifikansi 0. 05 iii. Hipotesis H 0 diterima jika: z ≥ -zα z ≥-1. 64 iv. Hitungan

Karena z=-4. 717 < -1. 64 maka H 0 ditolak d. k. l : Pernyataan apoteker itu tidak benar

SOAL Time : 15’ Batas ambang rata-rata kadar bahan pencemar yang diperbolehkan adalah 25. Dari hasil pengumpulan sampel air ledeng suatu kota didapatkan : 30 20 25 21 24 18 10 15 12 Dapatkah dikatakan bahwa air ledeng kota tersebut sudah tercemar? Anggap tingkat signifikansi 0. 05 dan diketahui z(0. 05)=1. 64