UJI HIPOTESIS ANALISIS BIVARIAT TABEL UJI HIPOTESIS KOMPARATIF

UJI HIPOTESIS ANALISIS BIVARIAT

TABEL UJI HIPOTESIS KOMPARATIF MACAM DATA DUA KELOMPOK DESKRIPTIF berpasangan Kategorik (Nominal, ordinal) Kategorik (ordinal) Numerik (Interval &rasio) Tidak berpasangan Mc Nemar Run test T-test Ø Sign test Ø Wilcoxon Related T-Test > 2 KELOMPOK berpasangan Tidak berpasangan Ø Koefisien kontingensi Ø Lambda Ø Eta Square Cochran Q Ø Median test Ø Mann-whiteney Ø Kolmogorov smirnov Ø Uji wald Independent T- test Ø Friedman Ø Two-way anova Ø One-way annova Ø Two- way annova ASOSIATIF (KORELATIF) Ø Median extension Ø Kruskalwalis Ø One way annova Ø One-way annova Ø Two- way annova Ø Spearman Ø Kendall’s tau Ø Korelasi product moment Ø Pearson Ø Korelasi parsial Ø Korelasi ganda Ø Regresi sederhana & ganda

UJI HIPOTESIS KOMPARATIF VARIABEL NUMERIK 2 KELOMPOK Tujuan : • Mencari perbedaan antara 2 kelompok Variabel : • Dependent : Numerik • Independent : Kategorik

Uji T Tidak berpasangan (independent T-Test) Tujuan : • Mencari perbedaan antara 2 kelompok independent. Contoh kasus : • Apakah ada perbedaan antara skor anxietas wiraswasta dengan karyawan swasta?

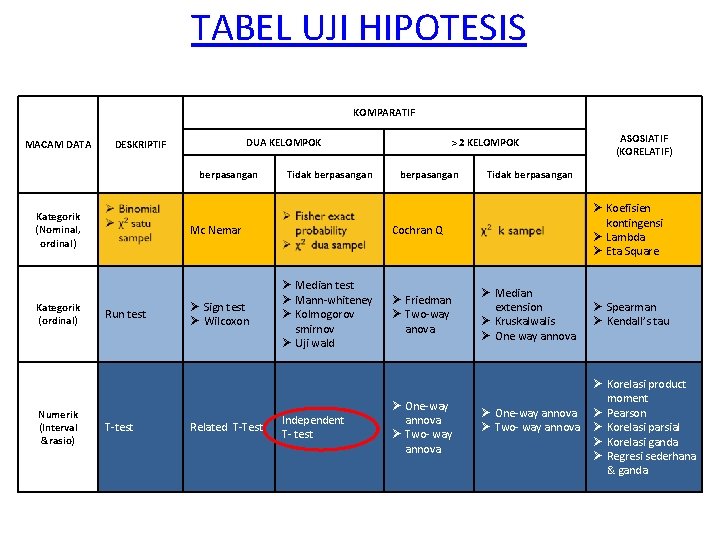
TABEL UJI HIPOTESIS KOMPARATIF MACAM DATA DUA KELOMPOK DESKRIPTIF berpasangan Kategorik (Nominal, ordinal) Kategorik (ordinal) Numerik (Interval &rasio) Tidak berpasangan Mc Nemar Run test T-test Ø Sign test Ø Wilcoxon Related T-Test > 2 KELOMPOK berpasangan Tidak berpasangan Ø Koefisien kontingensi Ø Lambda Ø Eta Square Cochran Q Ø Median test Ø Mann-whiteney Ø Kolmogorov smirnov Ø Uji wald Independent T- test Ø Friedman Ø Two-way anova Ø One-way annova Ø Two- way annova ASOSIATIF (KORELATIF) Ø Median extension Ø Kruskalwalis Ø One way annova Ø One-way annova Ø Two- way annova Ø Spearman Ø Kendall’s tau Ø Korelasi product moment Ø Pearson Ø Korelasi parsial Ø Korelasi ganda Ø Regresi sederhana & ganda

Syarat Independent T-test

SPSS Analyze • - Compare Means • - Independent Sample T-test • Pada Test variable(s) masukkan variabel numerik • Pada Grouping variable masukkan variabel kategori • Klik grouping variable : tuliskan nilai kategori variabel

Interpretasi output Karena nilai P < 0, 05, maka dapat diambil kesimpulan “terdapat berbedaan” rerata skor ansietas yang bermakna antara orang yang bekerja sebagai wiraswasta dan karyawan swasta dimana skor ansietas orang yang bekerja sebagai pengusaha lebih rendah daripada skor ansietas orang yang bekerja sebagai karyawan swasta

Uji Hipotesis Korelatif

Uji Koefisien Kontingensi dan Lambda Tujuan : • Mencari Korelasi atau hubungan antara 2 variabel kategorik Contoh kasus : • Apakah terdapat korelasi antara perilaku merokok dengan produktifitas pekerja?

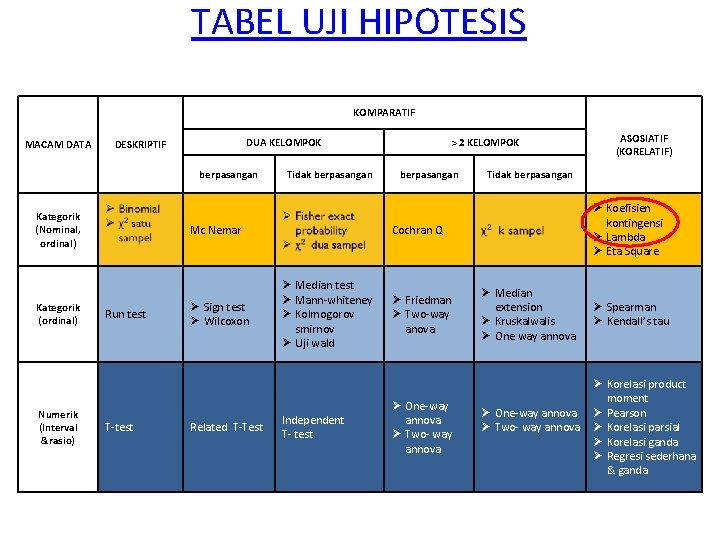
TABEL UJI HIPOTESIS KOMPARATIF MACAM DATA DUA KELOMPOK DESKRIPTIF berpasangan Kategorik (Nominal, ordinal) Kategorik (ordinal) Numerik (Interval &rasio) Tidak berpasangan Mc Nemar Run test T-test Ø Sign test Ø Wilcoxon Related T-Test > 2 KELOMPOK berpasangan Tidak berpasangan Ø Koefisien kontingensi Ø Lambda Ø Eta Square Cochran Q Ø Median test Ø Mann-whiteney Ø Kolmogorov smirnov Ø Uji wald Independent T- test Ø Friedman Ø Two-way anova Ø One-way annova Ø Two- way annova ASOSIATIF (KORELATIF) Ø Median extension Ø Kruskalwalis Ø One way annova Ø One-way annova Ø Two- way annova Ø Spearman Ø Kendall’s tau Ø Korelasi product moment Ø Pearson Ø Korelasi parsial Ø Korelasi ganda Ø Regresi sederhana & ganda

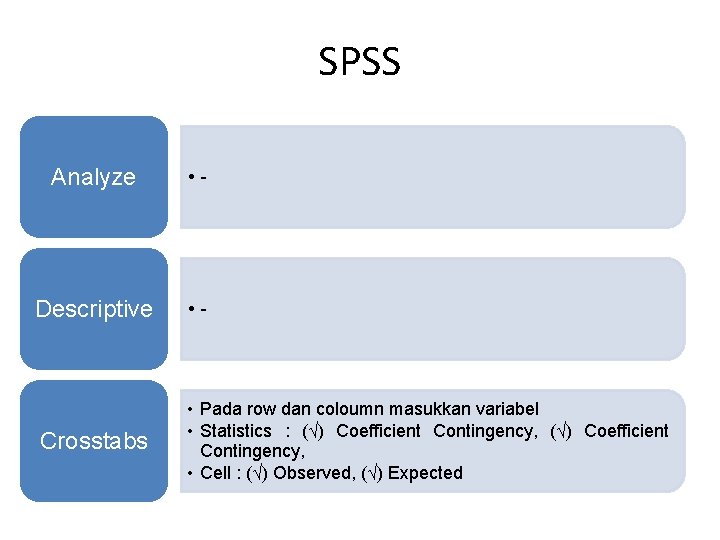
SPSS Analyze • - Descriptive • - Crosstabs • Pada row dan coloumn masukkan variabel • Statistics : (√) Coefficient Contingency, • Cell : (√) Observed, (√) Expected

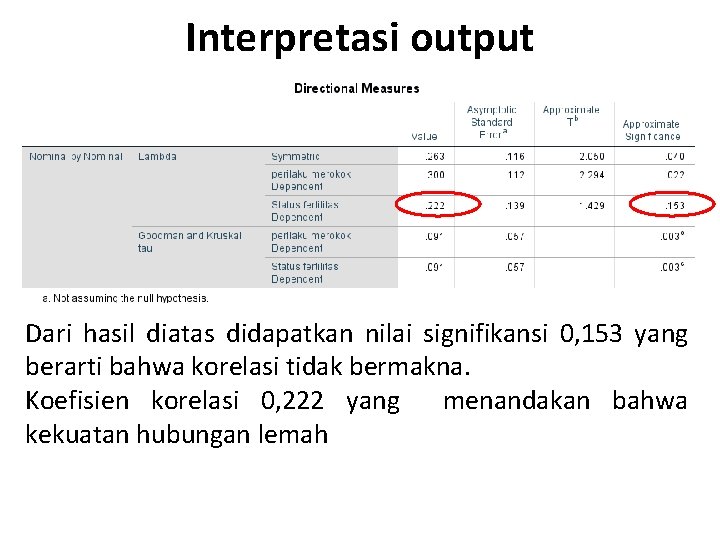
Interpretasi output Dari hasil diatas didapatkan nilai signifikansi 0, 153 yang berarti bahwa korelasi tidak bermakna. Koefisien korelasi 0, 222 yang menandakan bahwa kekuatan hubungan lemah

Hasil uji koefisien kontingensi menunjukkan signifikansi 0, 003 yang menandakan bahwa korelasi bermakna dengan kekuatan hubungan sebesar 0, 289

Uji Pearson Tujuan : • Mencari Korelasi atau hubungan antara 2 variabel numerik Contoh kasus : • Apakah terdapat korelasi antara skor depresi dengan skor ansietas ?

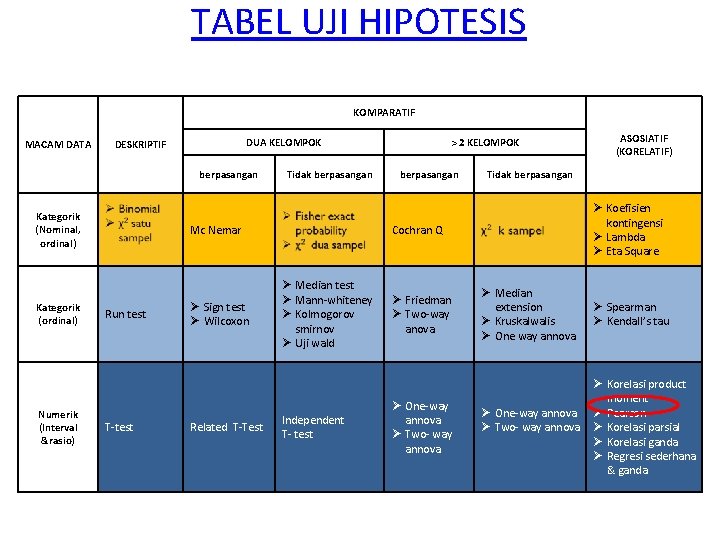
TABEL UJI HIPOTESIS KOMPARATIF MACAM DATA DUA KELOMPOK DESKRIPTIF berpasangan Kategorik (Nominal, ordinal) Kategorik (ordinal) Numerik (Interval &rasio) Tidak berpasangan Mc Nemar Run test T-test Ø Sign test Ø Wilcoxon Related T-Test > 2 KELOMPOK berpasangan Tidak berpasangan Ø Koefisien kontingensi Ø Lambda Ø Eta Square Cochran Q Ø Median test Ø Mann-whiteney Ø Kolmogorov smirnov Ø Uji wald Independent T- test Ø Friedman Ø Two-way anova Ø One-way annova Ø Two- way annova ASOSIATIF (KORELATIF) Ø Median extension Ø Kruskalwalis Ø One way annova Ø One-way annova Ø Two- way annova Ø Spearman Ø Kendall’s tau Ø Korelasi product moment Ø Pearson Ø Korelasi parsial Ø Korelasi ganda Ø Regresi sederhana & ganda

Alur uji

SPSS Analyze • - Corelate • - Bivariate • Masukkan kedua variabel pada kotak variables • Statistics : (√) pearson

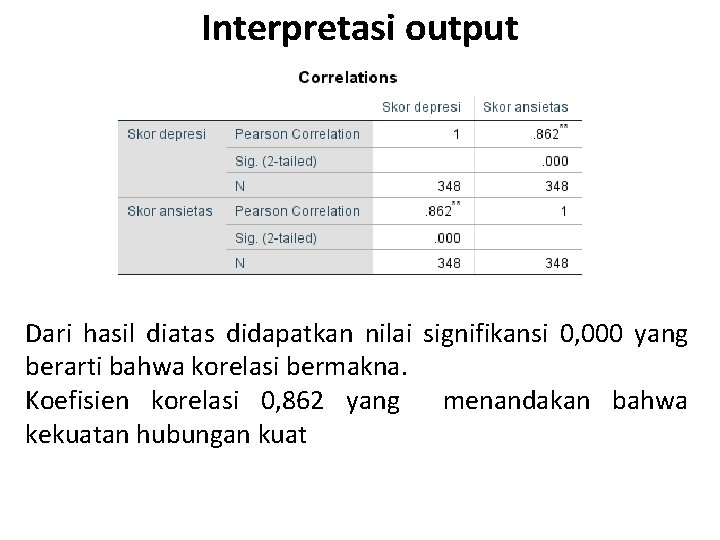
Interpretasi output Dari hasil diatas didapatkan nilai signifikansi 0, 000 yang berarti bahwa korelasi bermakna. Koefisien korelasi 0, 862 yang menandakan bahwa kekuatan hubungan kuat

Uji Spearman Tujuan : • Mencari Korelasi atau hubungan antara 2 variabel numerik jika data tidak terdistribusi normal Contoh kasus : • Apakah terdapat korelasi antara skor gangguan somatik dengan skor gangguan sosial ?

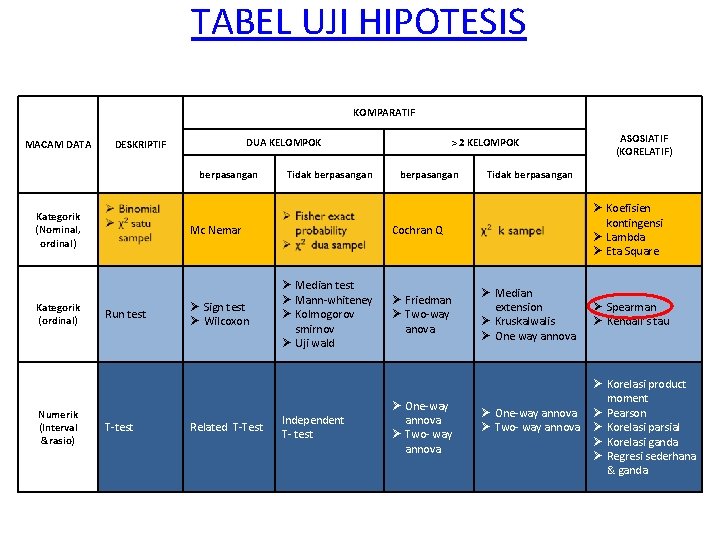
TABEL UJI HIPOTESIS KOMPARATIF MACAM DATA DUA KELOMPOK DESKRIPTIF berpasangan Kategorik (Nominal, ordinal) Kategorik (ordinal) Numerik (Interval &rasio) Tidak berpasangan Mc Nemar Run test T-test Ø Sign test Ø Wilcoxon Related T-Test > 2 KELOMPOK berpasangan Tidak berpasangan Ø Koefisien kontingensi Ø Lambda Ø Eta Square Cochran Q Ø Median test Ø Mann-whiteney Ø Kolmogorov smirnov Ø Uji wald Independent T- test Ø Friedman Ø Two-way anova Ø One-way annova Ø Two- way annova ASOSIATIF (KORELATIF) Ø Median extension Ø Kruskalwalis Ø One way annova Ø One-way annova Ø Two- way annova Ø Spearman Ø Kendall’s tau Ø Korelasi product moment Ø Pearson Ø Korelasi parsial Ø Korelasi ganda Ø Regresi sederhana & ganda

Alur uji

SPSS Analyze • - Corelate • - Bivariate • Masukkan kedua variabel pada kotak variables • Statistics : (√) spearman

Interpretasi output Dari hasil diatas didapatkan nilai signifikansi 0, 000 yang berarti bahwa korelasi bermakna. Koefisien korelasi 0, 351 yang menandakan bahwa kekuatan hubungan lemah