Ugicie belek elbetowych Janusz Pdziwiatr 1 Podstawy teoretyczne

Ugięcie belek żelbetowych Janusz Pędziwiatr 1

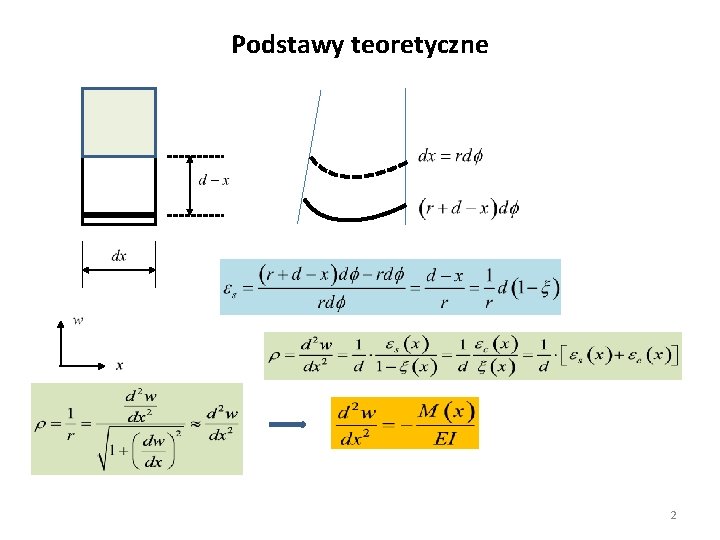
Podstawy teoretyczne 2

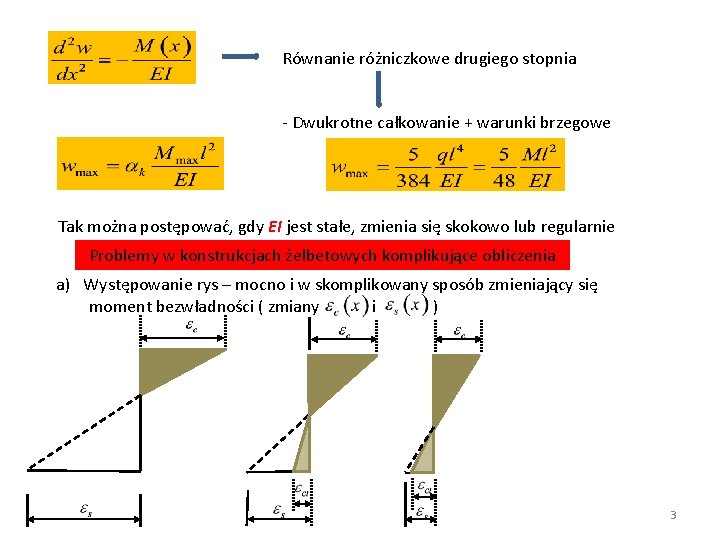
Równanie różniczkowe drugiego stopnia - Dwukrotne całkowanie + warunki brzegowe Tak można postępować, gdy EI jest stałe, zmienia się skokowo lub regularnie Problemy w konstrukcjach żelbetowych komplikujące obliczenia a) Występowanie rys – mocno i w skomplikowany sposób zmieniający się moment bezwładności ( zmiany i ) 3

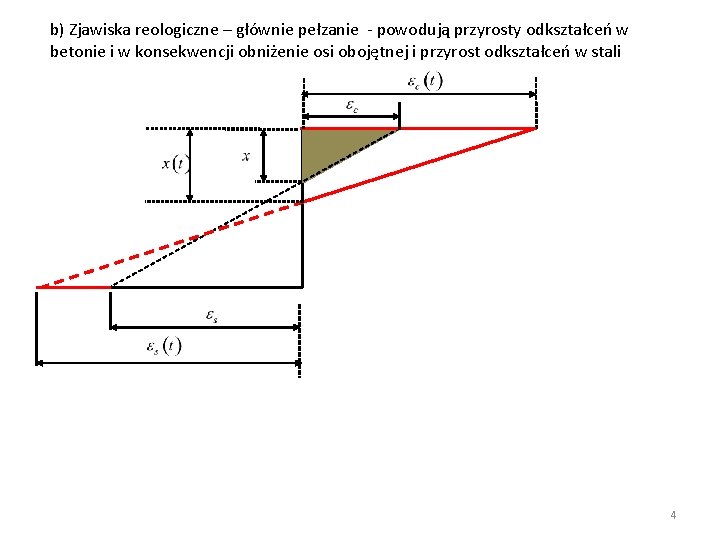
b) Zjawiska reologiczne – głównie pełzanie - powodują przyrosty odkształceń w betonie i w konsekwencji obniżenie osi obojętnej i przyrost odkształceń w stali 4

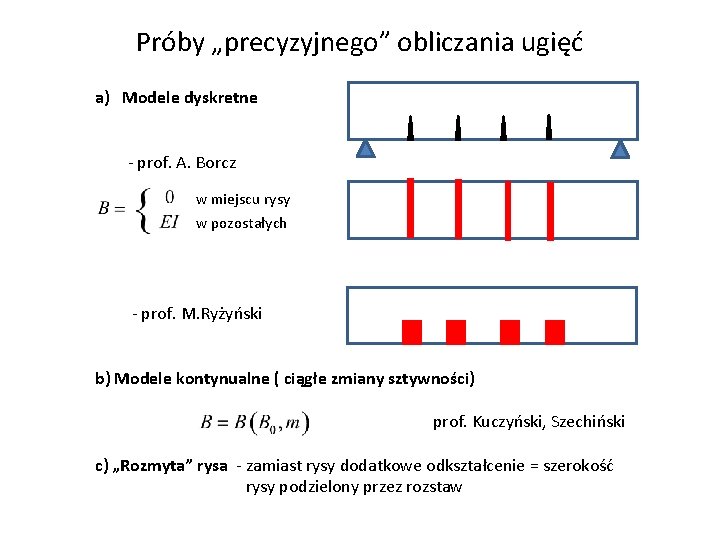
Próby „precyzyjnego” obliczania ugięć a) Modele dyskretne - prof. A. Borcz w miejscu rysy w pozostałych - prof. M. Ryżyński b) Modele kontynualne ( ciągłe zmiany sztywności) prof. Kuczyński, Szechiński c) „Rozmyta” rysa - zamiast rysy dodatkowe odkształcenie = szerokość rysy podzielony przez rozstaw

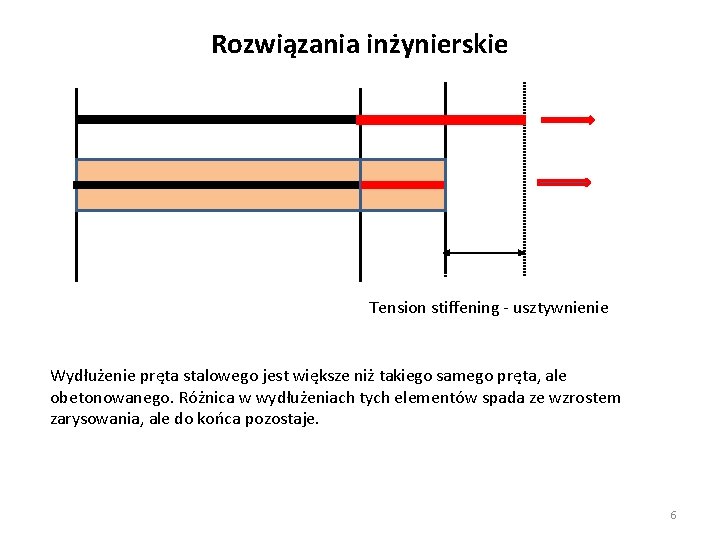
Rozwiązania inżynierskie Tension stiffening - usztywnienie Wydłużenie pręta stalowego jest większe niż takiego samego pręta, ale obetonowanego. Różnica w wydłużeniach tych elementów spada ze wzrostem zarysowania, ale do końca pozostaje. 6

Różne koncepcje inżynierskie a) Teoria Muraszewa ( i inne podobne) a) Belka przy zwiększających się obciążeniach pracuje kolejno w trzech fazach – I , Ia , II. b) Fazom tym odpowiadające trzy różne sztywności belki c) Sztywność ta obejmuje całą belkę ( całe przęsło) – decyduje wartość maksymalnego momentu b) Norma amerykańska ( ACI 318) • „Średni” moment bezwładności • Pełzanie – obliczone ugięcie strefie ściskanej , , ; uwzględnia się wpływ zbrojenia w 7

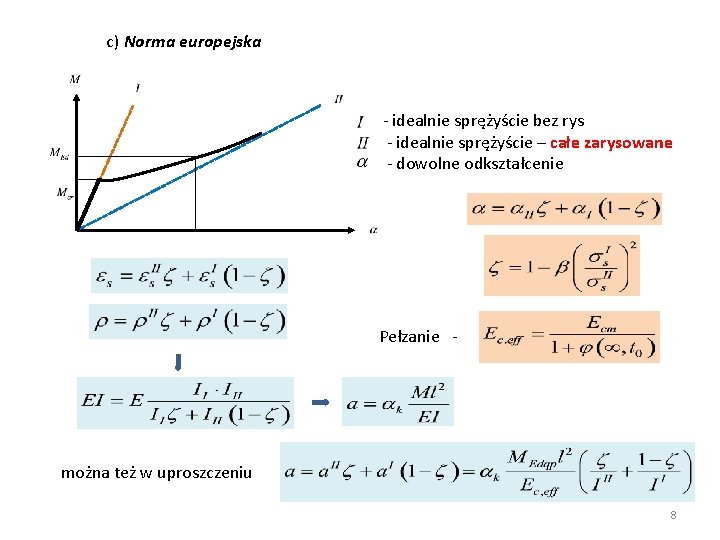
c) Norma europejska - idealnie sprężyście bez rys - idealnie sprężyście – całe zarysowane - dowolne odkształcenie Pełzanie - można też w uproszczeniu 8

Obliczanie ugięć i zarysowania – tok postępowania 1. Czynności wstępne - wyznaczenie maksymalnego momentu przęsłowego wywołanego kombinacją obciążeń prawie stałych Uwaga: czasami należy wybrać inną kombinację obciążeń: - częstą i - podstawową charakterystyczną i i - wyznaczenie końcowej wartości współczynnika pełzania i efektywnego modułu sprężystości 9

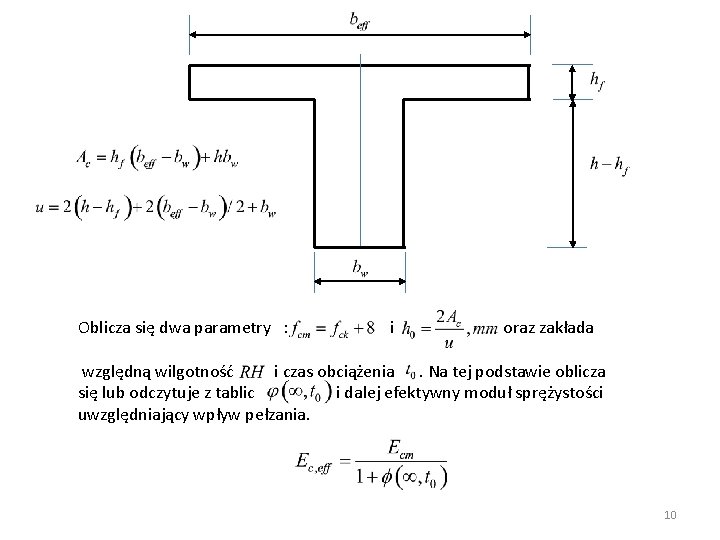
Oblicza się dwa parametry : i oraz zakłada względną wilgotność i czas obciążenia. Na tej podstawie oblicza się lub odczytuje z tablic i dalej efektywny moduł sprężystości uwzględniający wpływ pełzania. 10

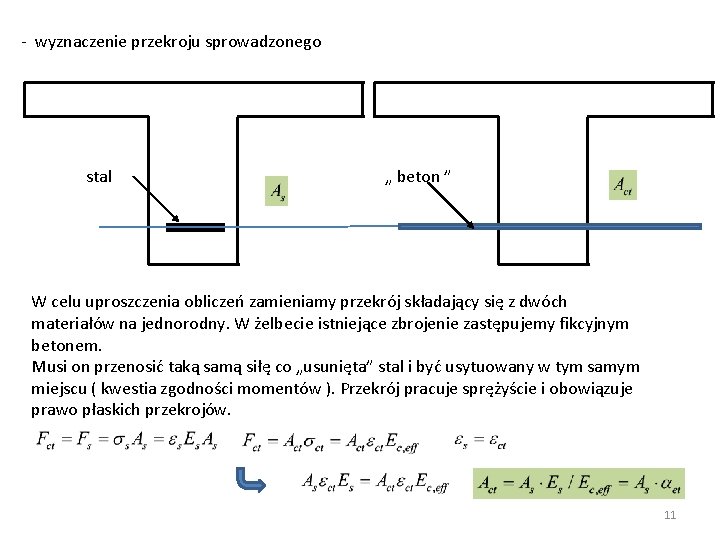
- wyznaczenie przekroju sprowadzonego stal „ beton ” W celu uproszczenia obliczeń zamieniamy przekrój składający się z dwóch materiałów na jednorodny. W żelbecie istniejące zbrojenie zastępujemy fikcyjnym betonem. Musi on przenosić taką samą siłę co „usunięta” stal i być usytuowany w tym samym miejscu ( kwestia zgodności momentów ). Przekrój pracuje sprężyście i obowiązuje prawo płaskich przekrojów. 11

Przekrój pracuje w fazie I Cele – wyznaczenie , sprawdzenie, czy pojawią się rysy; ewentualne wyznaczenie ugięcia belki niezarysowanej a) Wyznaczenie pola przekroju sprowadzonego b) Obliczenie momentu statycznego względem np. górnej krawędzi c) Znalezienie środka ciężkości ( zasięgu strefy ściskanej) d) Obliczenie momentu bezwładności przekroju względem środka jego ciężkości e) Obliczenie wskaźnika na zginanie względem skrajnych włókien rozciąganych f) Sprawdzenie, czy nastąpi zarysowanie g) Przy braku rys – obliczenie ugięcia 12

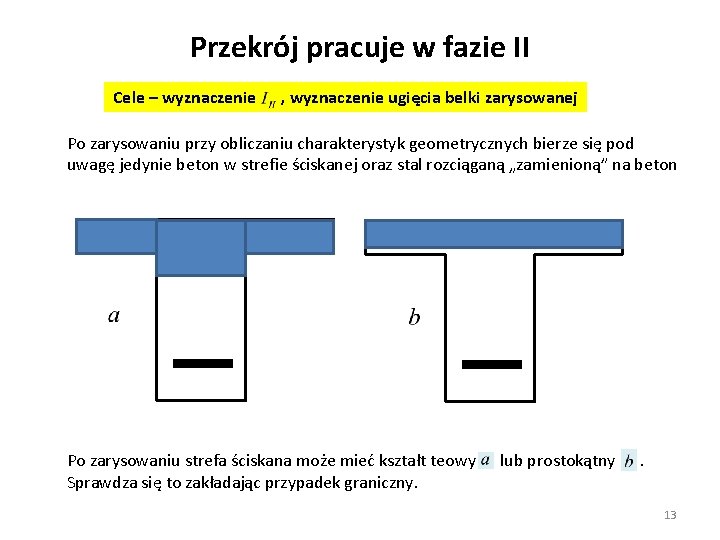
Przekrój pracuje w fazie II Cele – wyznaczenie , wyznaczenie ugięcia belki zarysowanej Po zarysowaniu przy obliczaniu charakterystyk geometrycznych bierze się pod uwagę jedynie beton w strefie ściskanej oraz stal rozciąganą „zamienioną” na beton Po zarysowaniu strefa ściskana może mieć kształt teowy Sprawdza się to zakładając przypadek graniczny. lub prostokątny . 13

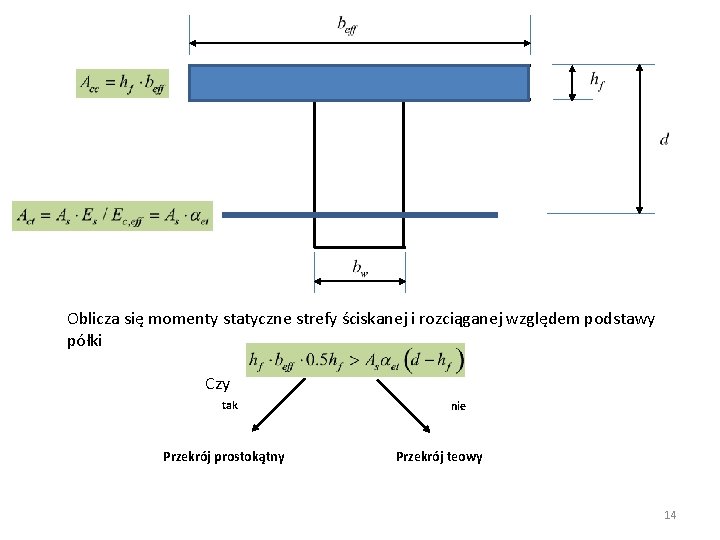
Oblicza się momenty statyczne strefy ściskanej i rozciąganej względem podstawy półki Czy tak Przekrój prostokątny nie Przekrój teowy 14

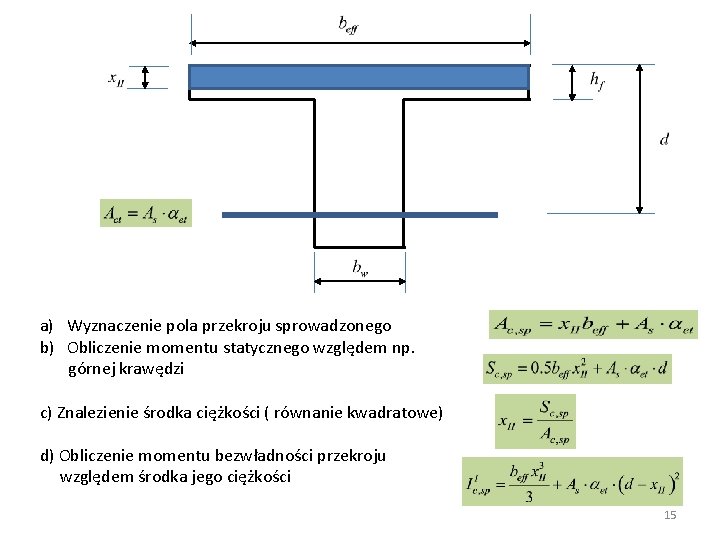
a) Wyznaczenie pola przekroju sprowadzonego b) Obliczenie momentu statycznego względem np. górnej krawędzi c) Znalezienie środka ciężkości ( równanie kwadratowe) d) Obliczenie momentu bezwładności przekroju względem środka jego ciężkości 15

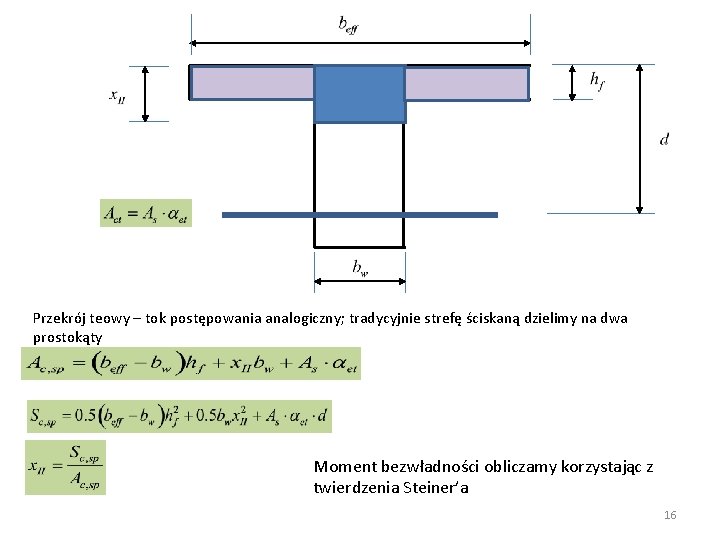
Przekrój teowy – tok postępowania analogiczny; tradycyjnie strefę ściskaną dzielimy na dwa prostokąty Moment bezwładności obliczamy korzystając z twierdzenia Steiner’a 16

Uwagi końcowe a) W wyniku zarysowania „wypada” beton ze strefy rozciąganej – w konsekwencji środek ciężkości przesuwa się ku górze. b) Kolejną konsekwencją zarysowania jest znaczny spadek wartości momentu bezwładności. Im mniejszy stopień zbrojenia tym spadek ten jest większy. Po zarysowaniu zbrojenie może mieć 70 -80% udział w sztywności. c) Końcową wartość ugięcia oblicza się z lub dokładniej d) W typowych sytuacjach obliczone ugięcie porównuje się z dopuszczalnym równym. e) Czasami zaleca się obliczać ugięcie wywołane jedynie obciążeniami użytkowymi. Wtedy dopuszczalne ugięcie jest o połowę mniejsze. 17