UE THERMODYNAMIQUE GENERALE LICENCE 3 DE SCIENCES PHYSIQUES

UE: THERMODYNAMIQUE GENERALE LICENCE 3 DE SCIENCES PHYSIQUES ET DE CHIMIE PROFESSEUR OUATTARA LASSINE Professeur OUATTARA LASSINE 1

FONCTION THERMODYNAMIQUE DES SYSTEMES MONOPHASES OUVERTS NON REAGISSANT RELATIONS GENERALES I. Potentiel chimique et variation des fonctions thermodynamiques 1. Fonctions thermodynamique A on associe une grandeur partielle molaire définie par : On définit ainsi l’enthalpie partielle molaire par : avec : potentiel chimique du constituant i. En opérant à T et P constants, la relation d’Euler permet d’écrire : Professeur OUATTARA LASSINE 2

Les autres fonctions peuvent se déduire de G. . Prenons l’énergie interne et étudions sa variation par rapport aux variables extensives S, V et Professeur OUATTARA LASSINE 3

Prenons la différentielle de E dans le cas général : on déduit : partant de Equation de Gibbs-Duhem généralisée on a Connaissant la différentielle de E, on a : Professeur OUATTARA LASSINE 4

soit Pour On a Le potentiel chimique du constituant i peut s’exprimer dans tous les cas de la façon suivante : Ces formules permettent de relier le potentiel chimique à l’affinité chimique. Professeur OUATTARA LASSINE 5

La condition d’équilibre peut s’écrire : Dans le cas de plusieurs réactions on aura de même : La condition d’équilibre dans ces conditions est : avec Professeur OUATTARA LASSINE 6

2. Potentiel chimique d’un mélange gazeux Pour un gaz pur i, Pour un corps pur i, Dans le cas d’un mélange de gaz parfait : est la pression partielle du constituant i P 0=1 bar Professeur OUATTARA LASSINE 7

• Quelques lois relatives au mélange de gaz C’est la loi de LEDUC pour des gaz mélangés à même T et P. Le potentiel chimique s’exprime en fonction de la fraction molaire dans le cas d’un mélange de gaz parfait par : Professeur OUATTARA LASSINE 8

II. Mélange idéal – Mélange parfait 1. Mélange idéal Un mélange est idéal par rapport à i lorsque le potentiel chimique peut s’écrire de la façon suivante : Pour un mélange gazeux à faible pression Pour un mélange de gaz parfait 2. Mélange parfait C’est un mélange idéal qui se manifeste à basse pression. C’est un mélange pour lequel certaines grandeurs thermodynamiques sont nulles. Professeur OUATTARA LASSINE 9

Le volume de mélange L’enthalpie de mélange ou chaleur de mélange L’énergie interne de mélange Remarque: pour un mélange parfait, l’entropie de mélange n’est pas nulle. C’est le paradoxe de Gibbs. Professeur OUATTARA LASSINE 10

III. Mélange de gaz réels On peut définir un potentiel chimique d’excès car le mélange n’est pas parfait. idéal excès avec : fugacité de gaz i Professeur OUATTARA LASSINE 11

Pour les corps gazeux pur : (à pression faible, ici la pression Pi=Ptotal car i seul car gaz pur) (à pression élevée, ici la fugacité fi=f car i seul car gaz pur) Professeur OUATTARA LASSINE 12

IV. Potentiel chimique d’un corps condensé (solide ou liquide) Dans le cas des corps condensés, le potentiel chimique est défini dans des conditions extrêmement particulières : solutions diluées, pression faible. En considérant une phase gazeuse en équilibre avec la phase liquide, le potentiel chimique peut s’écrire : pour P 0 est la pression de vapeur du gaz i au dessus de la solution. Professeur OUATTARA LASSINE 13

On peut définir une solution idéale comme un mélange pour lequel le corps considéré comme solvant est en grande quantité (grand excès) par rapport aux constituants de la solution dans tout le domaine de concentration. Pour une telle solution loi de Henry est la fraction molaire du corps dissous i (faible) En solution infiniment diluée, la pression de vapeur du soluté est proportionnelle à sa fraction molaire : Professeur OUATTARA LASSINE 14

Dans le cas des pressions élevées, le potentiel chimique s’écrit : Pour le corps dissous i Pour le solvant Professeur OUATTARA LASSINE 15

LES SOLUTIONS La solution est composée d’un mélange de liquide et de gaz, d’un mélange de plusieurs liquides, d’un mélange de liquide et de solide et d’un mélange de solide formant des solutions solides. Pour un corps condensé, nous avons défini le potentiel chimique d’un constituant i dans un solvant à partir de sa phase vapeur au dessus de la solution. Dans ce chapitre, nous étudierons les solutions diluées (idéales), les solutions parfaites et les solutions réelles. Professeur OUATTARA LASSINE 16

LES SOLUTIONS La solution est composée: * d’un mélange de liquide et de gaz, * d’un mélange de plusieurs liquides, d’un mélange de liquide et de solide * d’un mélange de solide formant des solutions solides. Dans ce chapitre, nous étudierons: * les solutions diluées (idéales), * les solutions parfaites * les solutions réelles. Professeur OUATTARA LASSINE 17

I ETUDE DES SOLUTIONS DILUEES OU IDEALES 1 Lois relatives au corps dissous 1. 1 Loi de Henry On s’intéresse à la pression de vapeur du corps dissous dans la solution. A l’équilibre entre la phase vapeur et la solution, le potentiel chimique des deux phases est le même. Phase vapeur Phase liquide (solution) Professeur OUATTARA LASSINE 18

Remarque : -pour des pressions faibles, le terme est négligeable -pour des pressions élevées, il faut en tenir compte. Professeur OUATTARA LASSINE 19

Pour des pressions faibles, le facteur exponentiel devient une constante ne dépendant que de la température T d’où : Loi de Henry avec Cas particulier : : tension de vapeur de i à l’état pur Professeur OUATTARA LASSINE 20

1. 2 Variation de la solubilité d’un gaz avec la température. Il s’agit d’exprimer la variation de la solubilité d’un gaz en solution en fonction de la température. Au dessus de la solution, il y a une phase gazeuse. A l’équilibre entre la phase gazeuse et la phase liquide, le potentiel chimique est le même. Professeur OUATTARA LASSINE 21

Professeur OUATTARA LASSINE 22

1. 3 Variation de la solubilité des corps purs solides avec la température. On s’intéresse uniquement aux corps solides peu solubles. On veut déterminer la variation de la solubilité lorsque le corps solide sature la solution. A l’équilibre, le potentiel chimique du corps solide pur est égal à celui du corps dissous : Professeur OUATTARA LASSINE 23

Corps pur solide Corps pur dissous en solution après avoir appliqué la relation de Gibbs Helmholtz. La solubilité augmente quand la température augmente Professeur OUATTARA LASSINE 24

1. 4 Loi de distribution de Nernst ou de coefficient de partage. On considère un corps soluble dans deux solvants non miscibles en contact entre eux. A l’équilibre, le potentiel chimique du constituant i dans la zone de séparation sera le même pour les deux phases. Le potentiel chimique du constituant i dans le solvant 1 est égal au potentiel chimique du constituant i dans le solvant 2. Professeur OUATTARA LASSINE 25

Professeur OUATTARA LASSINE 26

2. Lois relatives au solvant 2. 1 Loi de pression osmotique de Vant’Hoff. Soit une solution contenant un soluté i de fraction molaire séparé par une membrane semi perméable (perméable au seul solvant) d’une certaine quantité de solvant pur à la même température T. Membrane semi perméable Psl Remarque : Les deux compartiments contiennent le même solvant Ps Solution contenant i Solvant pur A l’équilibre, le potentiel chimique du solvant est le même dans les deux compartiments. Comme la température est la même, l’égalité ne peut être établie que si les pressions des liquides sont différentes Professeur OUATTARA LASSINE 27

Car pour les solutions diluées ( En posant w est la pression osmotique. Elle représente la différence de pression entre les deux compartiments lorsque le système est à l’équilibre. Elle dépend de la fraction molaire du solvant dans le compartiment qui contient la solution. Professeur OUATTARA LASSINE 28

Dans la mesure où la solution contient plusieurs solutés et comme la solution est diluée, on peut écrire : soit à partir de la molarité de i on a : Très faible devant celui du solvant Donc avec soit donc formule osmotique de Vant’Hoff. Professeur OUATTARA LASSINE 29

2. 1 Volume partiel molaire du solvant et chaleur de dilution dans le cas d’une solution diluée 2. 2. 1 Volume partiel molaire du solvant Pour le solvant Dans le cas d’une solution très diluée, le volume partiel molaire du solvant est égal au volume molaire du solvant. Volume de mélange est nul Professeur OUATTARA LASSINE 30

2. 2. 2 Chaleur de dilution d’une solution diluée On dérive l’expression ci-dessus par rapport à T en maintenant P et s fixes Entropie partielle molaire de mélange non nulle. soit Enthalpie molaire de dilution Soit Si on a une solution très diluée et qu’on ajoute du solvant, il n’y a pas d’effet thermique Professeur OUATTARA LASSINE 31

2. 3 Loi Tonométrique de Raoult Cette loi est relative à la pression de vapeur du solvant dans la solution PS. A l’équilibre on écrit : Phase liquide Si Donc Phase gazeuse alors loi de Raoult : tension de vapeur saturante du solvant ou pression de vapeur du solvant à l’état pur. C’est aussi une tension standard. Professeur OUATTARA LASSINE 32

On emploie souvent l’abaissement tonométrique relatif : Pour un seul corps dissous i dans une solution binaire : Constante tonométrique avec On en tire la masse molaire du soluté Professeur OUATTARA LASSINE 33

2. 4 Loi ébulliométrique de Raoult Cette loi est valable quand le solvant est très volatil et au dessus de la solution toute la vapeur est celle du solvant pur. Le corps dissous n’est pas volatil. Ici, on compare le point d’ébullition du solvant à celui de la solution. On opère à pression constante. La loi tonométrique de Raoult est valable quelle que soit la pression donc En utilisant la relation de Gibbs-Helmholtz, car Professeur OUATTARA LASSINE 34

avec chaleur de vaporisation La méthode ébulliométrique permet d’atteindre la masse molaire du corps dissous. La solution étant idéale, on peut écrire Solution idéale (très diluée) Pour une solution binaire (1 seul corps dissous), on a : : molalité de i (mol/kg solvant) Ms (g/mol) avec L’élévation ébulliométrique et Professeur OUATTARA LASSINE est la constante ébullioscopique 35

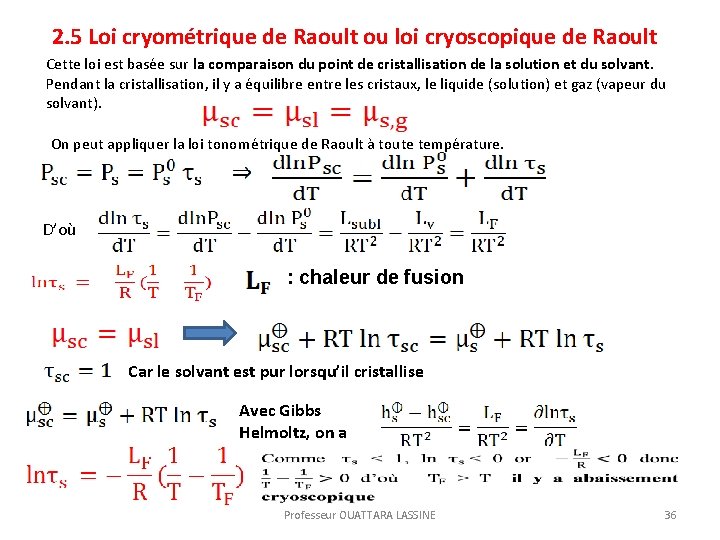
2. 5 Loi cryométrique de Raoult ou loi cryoscopique de Raoult Cette loi est basée sur la comparaison du point de cristallisation de la solution et du solvant. Pendant la cristallisation, il y a équilibre entre les cristaux, le liquide (solution) et gaz (vapeur du solvant). On peut appliquer la loi tonométrique de Raoult à toute température. D’où : chaleur de fusion Car le solvant est pur lorsqu’il cristallise Avec Gibbs Helmoltz, on a Professeur OUATTARA LASSINE 36

En procédant comme en ébulliomètrie, l’abaissement cryoscopique peut se mettre sous la forme : Abaissement cryoscopique Constante cryoscopique Professeur OUATTARA LASSINE 37

II ETUDE DES SOLUTIONS PARFAITES Les solutions parfaites sont des solutions idéales qui obéissent dans tout le domaine de composition à la loi de Raoult et de Henry. La tension de vapeur du soluté ou du solvant (système binaire) est proportionnelle à son titre où sa fraction molaire. Pour les solutions parfaites, la pression totale est aussi fonction du titre ou de la fraction molaire. Professeur OUATTARA LASSINE 38

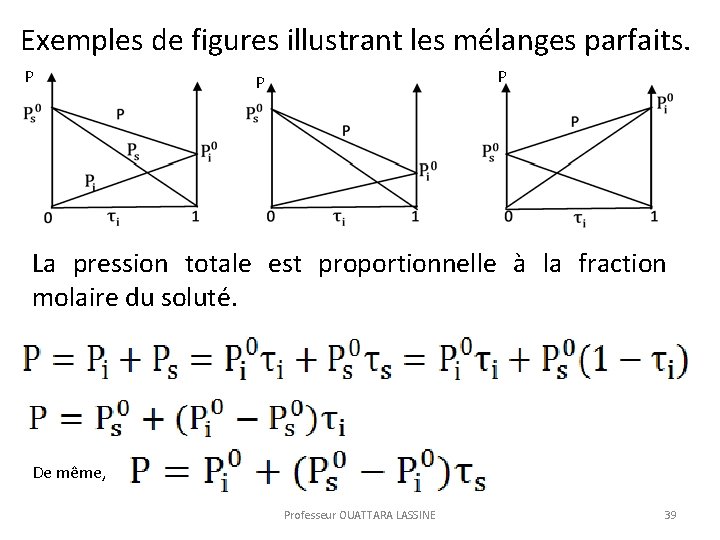
Exemples de figures illustrant les mélanges parfaits. P P P La pression totale est proportionnelle à la fraction molaire du soluté. De même, Professeur OUATTARA LASSINE 39

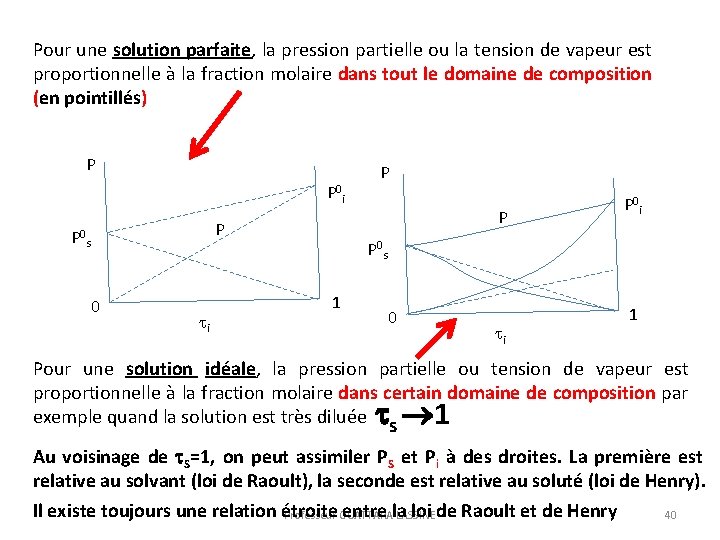
Pour une solution parfaite, la pression partielle ou la tension de vapeur est proportionnelle à la fraction molaire dans tout le domaine de composition (en pointillés) P P 0 i P P 0 s 0 i P P P 0 i P 0 s 1 0 i 1 Pour une solution idéale, la pression partielle ou tension de vapeur est proportionnelle à la fraction molaire dans certain domaine de composition par exemple quand la solution est très diluée s 1 Au voisinage de S=1, on peut assimiler PS et Pi à des droites. La première est relative au solvant (loi de Raoult), la seconde est relative au soluté (loi de Henry). Il existe toujours une relation étroite entre la loi de Raoult et de Henry Professeur OUATTARA LASSINE 40

III. SOLUTIONS RÉELLES III. 1 Système de référence On définit deux systèmes de référence pour les solutions réelles. Il s’agit du système de référence symétrique et du système de référence dissymétrique. Le système de référence symétrique est généralement employé lorsque toutes les espèces chimiques du système sont liquides à la température et sous la pression considérées. Dans la référence symétrique, chaque constituant est i 1 quand i 1 considéré à l’état pur. Pour cette référence, Le système de référence dissymétrique est employé principalement lorsque certains constituants n’existent pas sous forme liquide lorsqu’ils sont purs au voisinage de la pression et de la température d’intérêt. Ces constituants sont soit solides soit gazeux à l’état pur. Professeur OUATTARA LASSINE 41

Il est souvent impossible d’obtenir une solution avec une fraction molaire élevée de ses constituants. Ne pouvant observer l’état liquide pur, on distinguera le constituant majoritaire liquide dont la fraction molaire est la plus élevée qu’on désignera par solvants. Les autres constituants de fractions molaires plus faibles sont les solutés. La référence dissymétrique est telle que s 1 quand et i 1 quand (soluté) (solvant) La solution diluée (idéale) est pris comme système de référence (dissymétrique). Professeur OUATTARA LASSINE 42

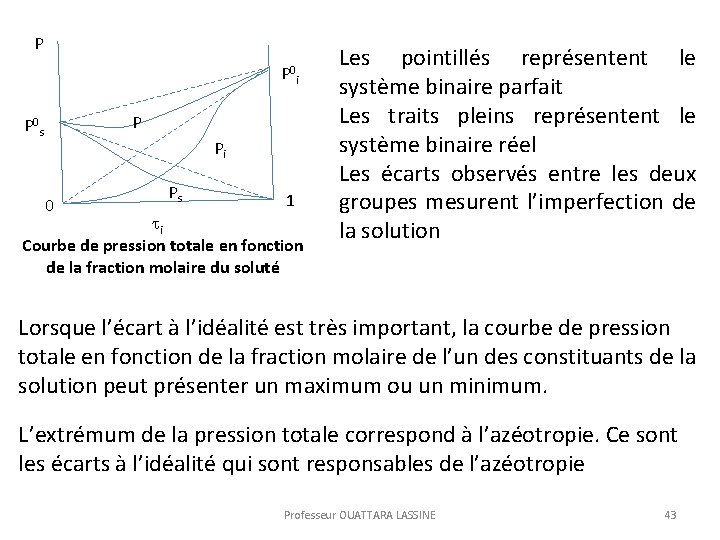
P P 0 i P P 0 s Pi 0 Ps 1 i Courbe de pression totale en fonction de la fraction molaire du soluté Les pointillés représentent le système binaire parfait Les traits pleins représentent le système binaire réel Les écarts observés entre les deux groupes mesurent l’imperfection de la solution Lorsque l’écart à l’idéalité est très important, la courbe de pression totale en fonction de la fraction molaire de l’un des constituants de la solution peut présenter un maximum ou un minimum. L’extrémum de la pression totale correspond à l’azéotropie. Ce sont les écarts à l’idéalité qui sont responsables de l’azéotropie Professeur OUATTARA LASSINE 43

Si la courbe de la pression totale passe par un extrémum (M), la fraction molaire est la même dans la phase gazeuse et dans la phase liquide. et P M L V 0 1 i On peut démontrer cela en partant de la relation de Gibbs. Duhem généralisée Professeur OUATTARA LASSINE 44

Et comme l’on opère à T constante et aussi comme la courbe de la pression totale passe par un extrémum, on a : d. T=0 et d. P=0. Ce qui conduit à: À l’équilibre, et avec D’où Or d. P=0=d. Pi+d. Ps donc D’où Professeur OUATTARA LASSINE 45

III. 2 ETUDES GENERALES DES SOLUTIONS RÉELLES Pour une solution réelle, terme idéal terme d’excès Généralisation de la loi de Henry et Raoult Nous utiliserons ici la référence symétrique En considérant la vapeur en équilibre avec la solution, nous avons : Professeur OUATTARA LASSINE 46

à pression constante P Pour on a Finalement : Professeur OUATTARA LASSINE 47

Pour le corps dissous : Loi de Henry avec : activité du constituant i : coefficient d’activité du constituant dissous i Pour le solvant : Loi de Raoult : activité du solvant dans la solution : coefficient d’activité du solvant Professeur OUATTARA LASSINE 48

Pour des solutions réelles très peu concentrées, on peut avoir : Loi Ebulliométrique Loi Cryométrique//Cryoscopique Les potentiels chimiques du soluté et du solvant sont : ; En utilisant la relation de Gibbs-Duhem, on peut établir la relation qui existe entre les coefficients d’activité d’une solution binaire réelle Professeur OUATTARA LASSINE 49

III. 3 Solutions semi-idéales Ce sont les solutions pour lesquelles le volume de mélange est nul ainsi que la chaleur de mélange c’est-à-dire que : et Le coefficient d’activité des solutions semi-idéales ne dépend pas de la pression et de la température mais dépend uniquement de la composition. III. 3. 1 : Influence de la pression ne dépend pas de la pression. Il en sera de même pour le coefficient d’activité Professeur OUATTARA LASSINE 50

III. 3. 2 : Influence de la température , d’après Gibbs-Helmoltz donc ne dépend pas de la température, il en est de même de c'est-à-dire Dans le cas d’une solution semi-idéale, le coefficient d’activité ne dépend pas de la pression et de la température, mais dépend uniquement de la composition. Professeur OUATTARA LASSINE 51

III. 4 Solutions régulières Ce sont des solutions non idéales pour lesquelles l’enthalpie de mélange et le volume de mélange ne sont pas nuls. Le phénomène de dissolution s’accompagne d’effet thermique et de chaleur de dilution. Ce sont les solutions pour lesquelles l’entropie d’excès est nulle c'est-à-dire que l’entropie d’excès de mélange est nulle. Professeur OUATTARA LASSINE 52

III. 4. 1 Expression de l’entropie de la solution réelle entropie idéale Pour les solutions régulières, l’entropie d’excès est nulle soit En réarrangeant l’expression précédente : Professeur OUATTARA LASSINE 53

III. 4. 2. Influence de la température Soit et comme soit Donc Dans les solutions régulières, la chaleur partielle de mélange est indépendante de la température. Professeur OUATTARA LASSINE 54

III. 5 Détermination expérimentale du coefficient d’activité a) Méthode directe *Lorsque le corps dissous est volatil, on mesure sa tension de vapeur et on détermine Loi de Henry *Lorsque c’est le solvant qui est volatil, on mesure la tension de vapeur du solvant au dessus de la solution Loi de Raoult Professeur OUATTARA LASSINE 55

*En exprimant l’activité en fonction de la chaleur de vaporisation du solvant, le coefficient d’activité s’obtient par : Méthode ébulliométrique Remarque : Si on peut écrire est de la forme *Pour la cryoscopie, l’activité du solvant s’exprime en fonction de la chaleur de fusion. Professeur OUATTARA LASSINE 56

Remarque : Pour les solutions diluées, la correction de dilution n’est pas nécessaire. Pour les solutions réelles, la correction de dilution est nécessaire. C'est-à-dire que si on détermine un coefficient d’activité à une température T et qu’on le ramène à une température uniforme (exemple t 1=25°C), on fait la correction de dilution de la façon suivante : on applique la relation de Gibbs-Helmoltz au solvant pur et à la solution ; Pour une solution semi-idéale très diluée, Pour les solutions réelles, Ls est la chaleur de dilution Professeur OUATTARA LASSINE 57

b. Méthode indirecte Elle est basée sur la relation de Gibbs-Duhem et permet de déterminer le coefficient d’activité du corps dissous. Comme alors soit d’où : La détermination de ln i se fait par intégration graphique de: Professeur OUATTARA LASSINE 58

III. 6 coefficient d’activité de l’électrolyte en solution aqueuse. Les solutions diluées d’électrolytes ont un caractère de solutions réelles car les forces d’interactions entre les différents ions et le solvant sont très importantes. Exemple de solutions électrolytiques : HCl, H 2 SO 4, CH 3 COOH, Na. OH, KOH, Na 2 SO 4, Na. Cl Professeur OUATTARA LASSINE 59

On distingue les électrolytes forts et faibles. Electrolytes forts : plus conducteurs d’électricité et se dissocient totalement Electrolytes faibles : moins conducteurs d’électricité et se dissocient partiellement. A ces deux types d’électrolytes, on peut appliquer la loi de cryoscopie: Pour les électrolytes forts, la constante cryoscopique est de la forme k’ = ν kc avec ν : le nombre d’ions. Aa Bb a A+ + b B- Professeur OUATTARA LASSINE 60

ν ions = a + b Dans le cas des électrolytes faibles, l’abaissement cryoscopique fait intervenir le degré de dissociation . Pour une mole d’électrolyte faible introduit, il apparait ions et il reste (1 -α) mole non dissociée. En tout, nous aurons [να+(1 -α) ]mole présente. Pour m moles introduites, on aura : [να+(1 -α) ]m ΔT=[να+(1 -α) ] k. C m Professeur OUATTARA LASSINE 61

Pour les électrolytes, particulièrement pour les électrolytes forts, on déterminera l’activité d’un électrolyte plutôt que l’activité d’un ion. Ainsi donc on déterminera le coefficient moyen d’activité des deux ions et non le coefficient d’activité individuel des ions. Professeur OUATTARA LASSINE 62

IV. LES RÉACTIONS CHIMIQUES I. GENERALITES Soit une réaction chimique d’équation stoechiométrique 1 2 et : sont les nombres de moles respectifs des réactifs et des produits formés Si la réaction est assez lente à tout instant, l’état du système peut être défini et son enthalpie libre serait: La variation élémentaire de l’enthalpie libre est: Professeur OUATTARA LASSINE 63

Supposons que l’évolution est spontanée et opérons à T et P constantes Comme et Dans notre hypothèse, ∆G Soit ∆G est l’enthalpie libre de la De même, on peut définir les autres grandeurs de réaction Professeur OUATTARA LASSINE 64

Affinité de la réaction chimique Posons: Dans l’hypothèse choisie, le processus est spontané, d. G < 0 ; d > 0 et ∆G<0 Pour A > 0 la réaction se fait dans le sens indiqué Pour A < 0 la réaction se fait dans le sens contraire Pour A = 0, ∆G=0 il y a équilibre Professeur OUATTARA LASSINE 65

IV. 2 LOI D’ACTION DE MASSE-CONSTANTE D’EQUILIBRE *Si nous considérons un mélange de gaz parfaits Dans un mélange gazeux, le potentiel chimique d’un gaz s’écrit: D’où A l’équilibre, d. G=0 soit ∆G=0 =-A ou A=0, on obtient Professeur OUATTARA LASSINE 66

Kp(T): Constante d’équilibre en phase gazeuse L’enthalpie libre standard de réaction se met sous la forme: *Si nous considérons un mélange de gaz réels Ici, on fait intervenir la fugacité. Ainsi, la constante d’équilibre peut se mettre sous la forme: Professeur OUATTARA LASSINE 67

Exprimons cette constante en fonction des fractions molaires: K On sait que: et avec D’où Exprimons cette constante en fonction des concentrations en molarité: KC Considérons le cas des solutions diluées Professeur OUATTARA LASSINE 68

IV. 3 Cas des solutions réelles Il faut faire intervenir les activités ai Professeur OUATTARA LASSINE 69

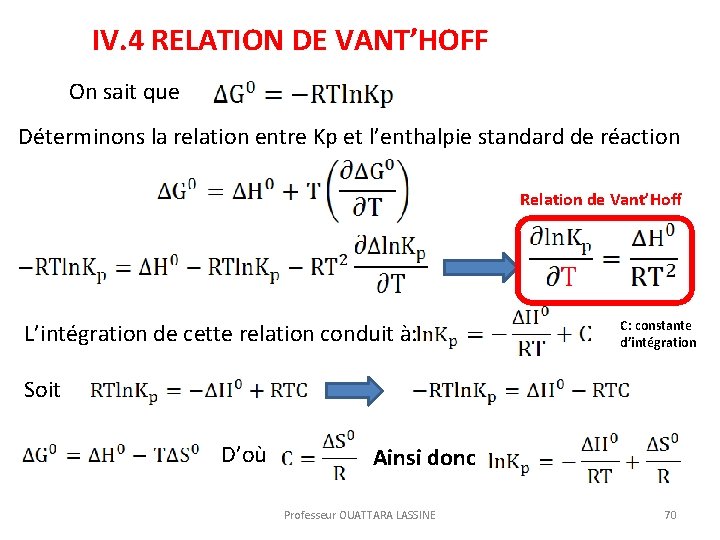
IV. 4 RELATION DE VANT’HOFF On sait que Déterminons la relation entre Kp et l’enthalpie standard de réaction Relation de Vant’Hoff L’intégration de cette relation conduit à: C: constante d’intégration Soit D’où Ainsi donc Professeur OUATTARA LASSINE 70

NB: les valeurs relatives à la formation d’un élément chimique dans l’état physique qui lui correspond aux conditions standards (P=1 atm; T=298 K) sont par définition nulles. Si les enthalpies et les entropies sont connues dans les conditions standards, ln. Kp peut être déterminé à n’importe quelle température Donc: et Et comme Peut dépendre de la température, on obtiendra Professeur OUATTARA LASSINE 71

Variation de KC dans le cas d’un mélange gazeux On rappelle que: La dérivée de l’expression ci-dessus par rapport à la température Or alors Professeur OUATTARA LASSINE 72

V Changement de phase de corps pur et règle de phase Lorsqu’une masse de corps pur passe d’un état physique à un autre, sous l’influence d’une variation de conditions extérieures, on dit qu’elle manifeste un changement d’état ou changement de phase. Qu’est ce qu’une phase ? C’est un milieu homogène, continu qui présente en tout point les mêmes propriétés physiques. Equilibre entre deux phases d’un corps pur. Pour une masse donnée d’un corps pur, on peut trouver les conditions de température et de pression pour lesquelles ce corps se présente sous forme de mélange hétérogène des deux phases en proportions quelconques. Les phases sont à l’équilibre et on a un équilibre hétérogène. Professeur OUATTARA LASSINE 73

1. La règle des phases de Gibbs La règle de phase de Gibbs fait intervenir arbitrairement le nombre de variables intensives dans l’étude d’un système en équilibre : variance (v). La variance d’un système thermodynamique est le nombre de variables indépendantes qui peuvent être modifiées sans que soient changés le nombre de phases et celui des constituants. Soit un système comportant c constituants, phases et r réactions chimiques autres que les réactions de passage. L’état du système sera déterminé si l’on connait la pression, la température et la composition chimique de chaque phase. La variance est aussi la différence entre le nombre de variables dont dépend l’état du système et le nombre de relations qui unissent ces variables. Professeur OUATTARA LASSINE 74

2. Quelques applications 2. 1. Systèmes unaires Pour les systèmes unaires, on a : c = 1 ; r = 0 ; donc Si on a =1 alors v=2 et le système est divariant. On peut se donner arbitrairement T, P. Le système est représenté par une seule phase (liquide, solide, vapeur). Professeur OUATTARA LASSINE 75

Si =2 on a v=1. Le système est monovariant. Il comporte deux phases (liquide et vapeur, solide et liquide, allotropie cristalline). On peut se donner arbitrairement : par exemple la pression alors T = f(P) par exemple la température alors P = f(T) Si =3 on a v=0 on a trois phases en présences : liquide, vapeur et solide et le système est invariant ou nulvariant. On ne peut pas se donner arbitrairement ni pression, ni température conformément à la règle de phase. Un tel équilibre entre les trois phases n’est obtenu que pour une température et une pression bien déterminées (point triple). Professeur OUATTARA LASSINE 76

Systèmes binaires C’est un système à deux constituants (c=2). Considérons un système à deux phases ( =2). Supposons qu’il n’y a pas de réactions chimiques r = 0 donc v=2+2 -2=2. Le système est divariant. On se donne arbitrairement deux variables intensives, par exemple, le titre ou la fraction molaire et la pression ainsi la température d’équilibre sera fonction de ces deux variables T = f( i, P). On peut aussi se donner i et T ainsi la pression d’équilibre P = f( i, T). Professeur OUATTARA LASSINE 77

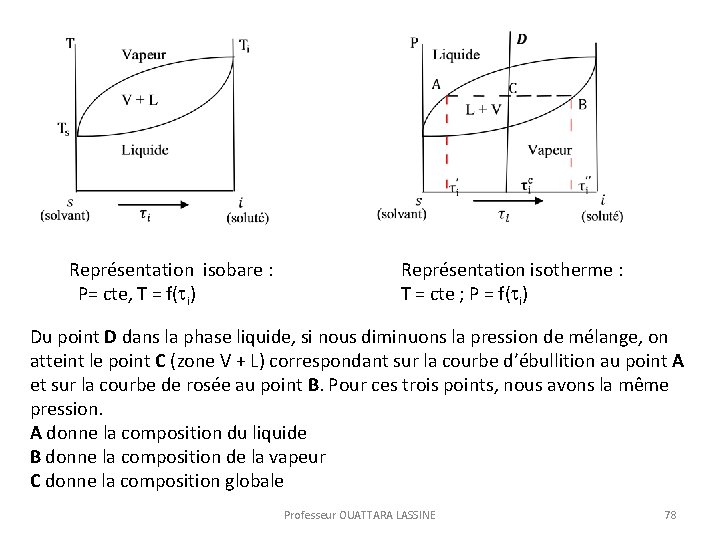
Représentation isobare : P= cte, T = f( i) Représentation isotherme : T = cte ; P = f( i) Du point D dans la phase liquide, si nous diminuons la pression de mélange, on atteint le point C (zone V + L) correspondant sur la courbe d’ébullition au point A et sur la courbe de rosée au point B. Pour ces trois points, nous avons la même pression. A donne la composition du liquide B donne la composition de la vapeur C donne la composition globale Professeur OUATTARA LASSINE 78

Calculons le rapport du nombre de moles dans les deux phases. Soit le nombre de moles dans la phase liquide le nombre de moles dans la phase vapeur : composition globale au point C Professeur OUATTARA LASSINE 79

Où et les fractions molaires de la phase liquide et de la phase vapeur. A l’équilibre entre liquide et vapeur : Professeur OUATTARA LASSINE 80

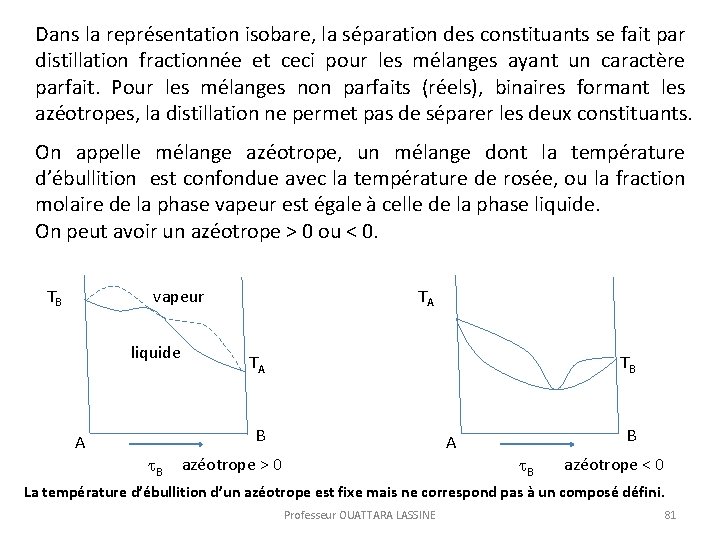
Dans la représentation isobare, la séparation des constituants se fait par distillation fractionnée et ceci pour les mélanges ayant un caractère parfait. Pour les mélanges non parfaits (réels), binaires formant les azéotropes, la distillation ne permet pas de séparer les deux constituants. On appelle mélange azéotrope, un mélange dont la température d’ébullition est confondue avec la température de rosée, ou la fraction molaire de la phase vapeur est égale à celle de la phase liquide. On peut avoir un azéotrope > 0 ou < 0. TB vapeur liquide TA TA TB B A azéotrope > 0 B azéotrope < 0 La température d’ébullition d’un azéotrope est fixe mais ne correspond pas à un composé défini. Professeur OUATTARA LASSINE 81

• Equilibre entre liquide et solide On a 2 constituants et 2 phases donc v=2. Le système est divariant Solidification des mélanges donnant une solution solide unique Partons d’un point M (composition connue), pris dans la zone du liquide et refroidissons: à T 1 la solidification commence et la composition du solide S 1 est différente de celle de L 1, la température continue à baisser et l’équilibre est toujours réalisé entre les deux phases. La solidification se termine à température T 2 quand le solide final S 2 a la même composition que le liquide initiale L 1. La dernière goutte du liquide a la composition L 2. Professeur OUATTARA LASSINE 82

Le refroidissement doit être lent pour que la diffusion dans le mélange homogénéise les cristaux. Si on arrête le refroidissement à une température T avant la solidification totale, le solide qui s’est déposé est plus riche en constituant le moins fusible, ici B, que le liquide initial. On le sépare, on le fond et on recommence l’opération, on se rapproche ainsi du constituant B. Equilibre entre liquide et solide ne formant pas de solution solide Nous avons deux constituants, deux phases et la réaction chimique nulle. V=2, le système est divariant. E La courbe TA E représente la courbe d’équilibre de la solution liquide et du solide A. La courbe TB E représente la courbe d’équilibre entre la solution liquide et le solide B. Le point E représente le point d’équilibre entre le liquide, les cristaux de A et de B. c’est le point Eutectique (de température TE et de composition E ). La température TE et la composition E sont toutes deux fonctions de la seule pression car le système binaire à trois phases monovariant. Professeur OUATTARA LASSINE 83

La courbe TA E représente la courbe d’équilibre de la solution liquide et du solide A. La courbe TB E représente la courbe d’équilibre entre la solution liquide et le solide B. Le point E représente le point d’équilibre entre le liquide, les cristaux de A et de B. c’est le point Eutectique (de température TE et de composition E ). La température TE et la composition E sont toutes deux fonctions de la seule pression car le système binaire à trois phases monovariant. Cas où il y a formation de produits nouveaux ou composés d’addition. Si les corps A et B réagissent pour former un composé d’addition, la variance est égale à 2 car nous avons : c = 3 ; r = 1 ; =2; v=2+3 -1 -2=2 L’existence du composé d’addition, ne modifie pas les variances Professeur OUATTARA LASSINE 84