Udavini su parametru sprendimas Paruo Vtrungs gimnazijos vyr

Uždavinių su parametru sprendimas Paruošė “Vėtrungės” gimnazijos vyr. mokytoja Rita Žukaitienė.

Lygtys su parametru l l Lygties su parametru prasmė yra tokia: kiekvieną parametro reikšmę atitinka tam tikra lygtis, t. y. lygtis su skaitiniais koeficientais. Lygties su keliais kintamaisiais vienus kintamuosius laikysime nežinomaisiais, o kitus parametrais. Kiekvieną tokią lygtį atitinka jos sprendinių aibė. Vadinasi, kiekvieną parametro reikšmę atitinka tam tikros lygties sprendinių aibė. Išspręsti lygtį su parametru a - vadinasi, kiekvienai a reikšmei rasti x reikšmes, tenkinančias šią lygtį.

Tiesinės lygtys Tiesinė lygtis su vienu kintamuoju ir vienu parametru yra f(a)x = g(a). Galimi tiesinės lygties f(a)x = g(a) atvejai: l 1) kai f(a) ≠ 0, tai tiesinės lygties sprendinys l l 2) kai f(a)=0, g(a)=0, tada lygtis virsta 0 ·x = 0, o tada lygties sprendiniai visi skaičiai; 3) kai f(a)=0, g(a)≠ 0, tada lygtis virsta 0·x=g(a) ir lygtis sprendinių neturi.

Sprendžiant tiesinę lygtį su parametru reikia nustatyti: l l l 1) su kuriomis parametrų reikšmėmis lygtis egzistuoja; 2) nustatyti, kaip nuo parametro priklauso sprendinys; 3) su kuriomis kintamojo reikšmėmis lygtis egzistuoja.

68. a) (p + 1)x = p; Jei p ≠ -1, tai x = p/(p + 1); Jei p = -1, tai 0·x = -1, lygtis sprendinių neturi. Atsakymas: x = p/(p + 1), kai p ≠ -1; neturi sprendinių, kai p = -1. b) px = p² + p + 1; Jei p ≠ 0, tai x = (p² + p +1)/p; Jei p = 0, tai 0·x = 1, lygtis sprendinių neturi. Atsakymas: x = (p² + p +1)/p, kai p ≠ 0; neturi sprendinių, kai p = 0.

c) (p² - 1)x = p + 1; Pertvarkome duotąją lygtį: (p -1)(p +1)x = p +1 Jei p ≠ -1, p ≠ 1, tai x = (p +1)/((p -1)(p +1)) x =1/(p -1); Jei p = -1, tai 0·x = 0 ir lygties sprendinys xbet koks realusis skaičius. Jei p = 1, tai 0·x = 2 ir lygtis sprendinių neturi. Atsakymas: x =1/(p -1), kai p ≠ -1 ir p ≠ 1; lygtis turi be galo daug sprendinių, kai p=-1; sprendinių nėra, kai p = 1.

d) (p²- 5 p + 6)x = p + 3; Sprendimas. (p - 2)(p - 3)x = p + 3; Jei p ≠ 2, p ≠ 3, tai x = (p +3)/ (p² - 5 p + 6); Jei p = 2, tai 0·x = 5, lygtis sprendinių neturi; Jei p = 3, tai 0·x = 6, lygtis sprendinių neturi. Atsakymas: x = (p +3)/ (p² - 5 p + 6), kai p ≠ 2, p ≠ 3; sprendinių nėra, kai p = 3 arba p = 2.

Sudėtingesnių lygčių su parametru pavyzdžiai. 1. Išspręskite lygtį: Pertvarkome lygtį: Lygtis turi prasmę, kai (1 + a)(2 + a) ≠ 0.

Duotoji lygtis turi sprendinius, kai a ≠ -1, a ≠ -2. Kai a ≠ -1, a ≠ -2, tai x + 3 a + 2 a² = 0, t. y. x = - 3 a - 2 a². Kai a =-1 arba a =-2, tai lygtis neturi sprendinių. Atsakymas: x= - 3 a - 2 a², jei a ≠ -1 ir a ≠ -2. sprendinių nėra, jei a = -1 arba a = -2.

Kvadratinės lygtys su parametru l l l Kvadratinė lygtis, kurios kintamojo koeficientas ir laisvasis narys arba nors vienas jų yra raidiniai dydžiai, vadinama kvadratine lygtimi su parametru. Kvadratinėje lygtyje su parametru svarbiausią vaidmenį atlieka koeficientas prie x². Jei jis nelygus nuliui, tai lygtis išlieka kvadratine ir ieškomi jos, kaip kvadratinės sprendiniai. Jei koeficientas prie x² lygus nuliui, ieškomas gaunamos pirmojo laipsnio lygties sprendinys.

Sprendžiant kvadratinę lygtį su vienu parametru reikia nustatyti: l l 1) su kuriomis parametro reikšmėmis lygties kairioji pusė egzistuoja; 2) kaip kvadratinės lygties sprendinys priklauso nuo parametro.

Pavyzdžiai: 1. Išspręskite lygtį a(a - 1)x² - (2 a - 1)x + 1 = 0. Sprendimas 1) Jei a = 0, tai duotoji lygtis yra tiesinė: x +1 = 0 ir x = -1; 2) Jei a = 1, tai duotoji yra -x +1 = 0 ; x = 1. 3) a ≠ 0 arba a ≠ 1 tada sprendžiame kvadratinę lygtį: D = (2 a -1)² - 4 a(a -1) = = 4 a² - 4 a +1 - 4 a² + 4 a =1.

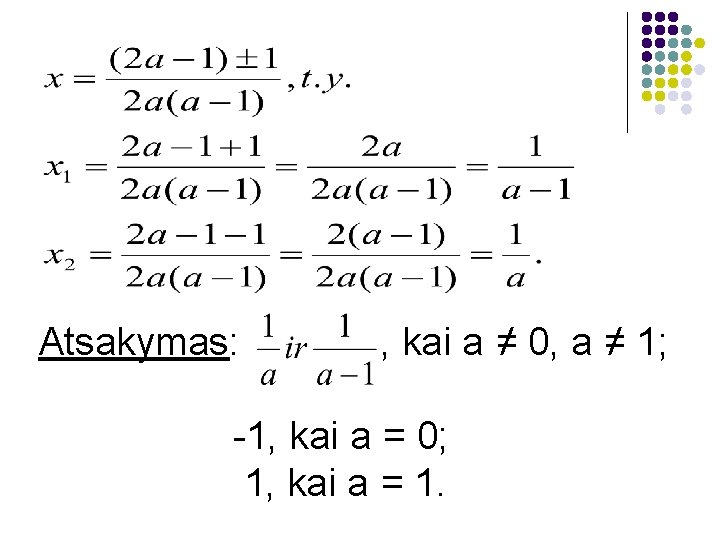
Atsakymas: , kai a ≠ 0, a ≠ 1; -1, kai a = 0; 1, kai a = 1.

2. Su kuriomis m reikšmėmis funkcija y = mx² - 2 mx + 4 įgyja tik teigiamas reikšmes? Sprendimas. Kai m = 0, tai funkcija pastovi: y = 4. Taigi jos reikšmė teigiama. Kai m ≠ 0, funkcija su visomis x reikšmėmis įgis teigiamas reikšmes tik tuo atveju, kai m > 0 ir diskriminantas D<0; Atsakymas.

Kai uždavinio sąlygoje prašo rasti parametro reikšmes su kuriomis kvadratinė lygtis su parametru neturi sprendinių, tai nagrinėjame tuos atvejus kai kvadratinė lygtis sprendinių neturi, t. y. D<0.

69. Su kuriomis k reikšmėmis lygtis neturi sprendinių: a) (2 - x)(x - 2) = k; (x - 2)² = - k; Lygtis neturi sprendinių, kai k>0. Atsakymas: sprendinių nėra, kai k>0. c)k²x² + 4 kx + 4 = 0; Kadangi neakcentuojama, kad reikia išspręsti kvadratinę lygtį , tai nagrinėjame šiuos atvejus: 1) Jei k = 0, tai 0·x = - 4 ir lygtis sprendinių neturi.

2) Jei k ≠ 0, tai turime kvadratinę lygtį, kurios koeficientai yra: a = k², b = 4 k, c = 4. D =16 k² - 16 k² =0. Lygtis sprendinių neturi, kai D<0. Ši nelygybė sprendinių neturi, todėl tokių k reikšmių nėra. Atsakymas. Tokių k reikšmių nėra.

b) 3 x² - 2 kx - k + 6 = 0; a = 3, b = - 2 k, c = - k + 6; D=(-2 k)² - 12 (- k + 6) = 4 k² + 12 k - 72; Lygtis sprendinių neturi, kai D < 0. Todėl sprendžiame kvadratinę nelygybę: k² + 3 k – 18 < 0; (k + 6)(k - 3) < 0; Išsprendę nelygybę intervalų metodu gauname, kad k priklauso intervalui (-6; 3). Atsakymas. (-6; 3).

d) x(x -1) + |k -1| = 0; Pertvarkome lygtį: x² - x + |k - 1| = 0; D = 1 - 4|k - 1|; Lygtis sprendinių neturi, kai D < 0, tai 1 - 4|k - 1| < 0; - 4|k - 1| < -1; |k - 1| >1/4; k – 1 > ¼ arba k -1 < - ¼ ; k > 1¼ k < ¾. Atsakymas. (-∞; ¾ )U(1¼ ; +∞).

70. Su kuriomis p reikšmėmis lygtis turi vieną sprendinį: a) (x + 1)(2 - x) = p; Pertvarkome lygtį: 2 x + 2 - x² - x - p = 0; -x² + x + 2 – p = 0; x² - x + p – 2 = 0; a =1, b = - 1, c = p – 2; D = 1 – 4(p – 2) =1 - 4 p + 8 = 9 - 4 p. Lygtis turi vieną sprendinį, kai D = 0. Tai 9 - 4 p = 0; 4 p = 9; p = 2¼. Atsakymas. 2¼.

b) x² - (p +1)x + p = - 4; Pertvarkome lygtį: x² - (p +1)x + p + 4 = 0; D=(p +1)²- 4(p + 4) =p² + 2 p +1 - 4 p -16 = p² - 2 p -15; Lygtis turi vieną sprendinį, kai D = 0. p² - 2 p -15 =0; D = 4 + 60 = 64 p = 5 ir p = - 3. Atsakymas. – 3; 5. c) x² + (2 - p)x – p - 3 = 0; D = (2 - p)² + 4(p + 3) = 4 - 4 p + p² + 4 p +12 = p² +16; Lygtis turi vieną sprendinį, kai D = 0. p² +16 = 0; p² = -16, sprendinių nėra. Atsakymas. Tokių p reikšmių nėra.

d) (p -1)x² + 2 px +(p +1) = 0; Kai p = 1, tai lygtis tampa tiesine ir 0·x + 2 x + 1= 0; 2 x + 2 = 0; x = -1. Kai p ≠ 1, tai turime kvadratinę lygtį: (p -1)x² + 2 px + (p +1) = 0; D = 4 p² - 4(p -1)(p +1) = 4 p² - 4 p² + 4 = 4. Kadangi D = 4, t. y. D > 0, tai lygtis turės du sprendinius. Atsakymas. 1.

71. Su kuriomis a reikšmėmis lygtis turi du sprendinius: a) (a + 3)x² - 2(a + 6)x + a +10 = 0; 1)Kai a = - 3, tai lygtis tampa tiesine ir ji turi vieną sprendinį. Tai ši reikšmė netinka. 2)Lygtis turi du sprendinius, kai D > 0. D = (- 2 a -12)² - 4(a + 3)(a +10) = 4 a² + 48 a + +144 - 4 a² - 12 a - 40 a - 120 = - 4 a + 24 > 0; 4 a < 24; a < 6. Atsakymas. (- ∞; - 3)U( - 3; 6).

b) (a - 3)x² + 2 x + 3 a = 11; (a - 3)x² + 2 x + 3 a -11 = 0; 1) Ši lygtis tampa tiesine ir turės tik vieną sprendinį, kai a = 3. Tai ši reikšmė mums netinka. 2) Kai a ≠ 3, tai D = 4 - 4(a - 3)( 3 a - 11) = - 12 a² + 80 a – 128. Lygtis turės du sprendinius, kai D > 0. - 12 a² + 80 a – 128 > 0|·(- 4); 3 a² - 20 a + 32 < 0; 3(a - 4)(a - 2⅔) < 0|: 3. Išsprendę intervalų metodu gauname intervalus (2⅔; 3)U(3; 4). Atsakymas. (2⅔; 3)U(3; 4).

c) (a -1)x² - 2(a + 1)x + a – 2 = 0 Lygtis tampa tiesine ir turi vieną sprendinį, kai a =1. Ši reikšmė mums netinka. Lygtis turi du sprendinius, kai D > 0. D =(- 2 a - 2)² - 4(a - 1)(a - 2) =4 a² + 8 a + 4 -4 a² + 12 a - 8 = 20 a – 4. Susidarome sistemą: Atsakymas. (1/5; 1)U(1; +∞).

d) x² + (|a - 1| - 1 )x = 0; Šios kvadratinės lygties a ≠ 0, tai lygtis turės du sprendinius, kai koeficientas b ≠ 0. x( x + (|a - 1| -1) = 0; x = 0 arba x + (|a - 1| -1 =0, Ši lygtis turi du sprendinius, kai |a - 1| - 1 ≠ 0; |a - 1| ≠ 1; a - 1 ≠ -1 arba a -1 ≠ 1, a ≠ 0, a ≠ 2. Atsakymas. (- ∞; 0)U(0; 2)U(2; +∞).

Modulinių lygčių su parametru sprendimas. 97. Su kuriomis p reikšmėmis lygtis turi bent vieną sprendinį: a) |x -1| + |2 x - 3| = p; Po moduliu esantys reiškiniai lygūs nuliui, kai x =1, 5. Šie taškai skaičių tiesę padalina į tris intervalus. Nagrinėdami lygtį kiekviename iš šių intervalų gauname tris sistemas: 1)

2)

Lygčių su dviem kintamaisiais sistemos

1) Lygčių sistema, kurios lygtyse yra parametras, vadinama lygčių sistema su parametru. 2) Sprendžiant tokią sistemą, reikia priklausomai nuo parametro rasti visus jos sprendinius arba įrodyti, kad jų nėra.

100. Nustatykite, su kuriomis parametrų a ir b reikšmėmis lygčių sistema turi be galo daug sprendinių: a)

101. Nustatykite, su kuriomis parametro a reikšmėmis lygčių sistema neturi sprendinių: Nagrinėsime atvejį, kai a = - ¼ ir gauname lygčių sistemą kuri sprendinių neturi. Atsakymas. a = - ¼.

Kai a = - 2, gauname lygčių sistemą kuri sprendinių neturi. Atsakymas. -2.

102. Nustatykite, su kuriomis parametro p reikšmėmis lygčių sistema turi sprendinių:

Uždavinių sprendimas iš 11 klasės uždavinyno. l 75. Išspręskite lygtį su parametru: a) (a + 2)x = a – 1; 1)Kai a + 2 ≠ 0, t. y. a ≠ -2, tai 2) Kai a = -2, tai 0·x = -3, tai lygtis sprendinių neturi. Atsakymas. kai a ≠ -2; sprendinių nėra, kai a = -2.

b) ax = a(a - 2); 1) Kai a ≠ 0, tai x = a - 2; 2) Kai a = 0, tai 0·x = 0 ir sprendiniai visi skaičiai. Atsakymas. x = a – 2, kai a ≠ 0; x - bet kuris realusis skaičius, kai a = 0. c)(a² - 4)x = a; (a - 2)(a + 2)x = 0; 1) Kai a ≠ ± 2, tai 2) Kai a = 2, tai 0·x = 2, lygtis sprendinių neturi; 3) Kai a = - 2, tai 0·x = - 2, lygtis sprendinių neturi. Atsakymas. kai a ≠ ± 2 Sprendinių nėra, kai a = 2, a = - 2.

d) (a² - 2 a + 1)x= a² + 2 a – 3; (a -1)²x = (a + 3)(a - 1); 1) Kai a ≠ 1, tai 2) Kai a = 1, tai 0·x = 0 ir sprendiniai visi skaičiai. Atsakymas. kai a ≠ 1 x - bet kuris realusis skaičius, kai a = 1.

e) (a³- a²- 4 a + 4)x = a – 1; Pertvarkome lygtį: (a -1)(a - 2)(a + 2)x = a -1; 1) Kai a ≠ 1, a ≠ ± 2, tai 2) Kai a = 1, tai 0·x = 0 ir sprendiniai visi skaičiai; 3) Kai a = 2, tai 0·x = 1 ir lygtis sprendinių neturi; 4) Kai a = -2, tai 0·x = - 3 ir lygtis sprendinių neturi. Atsakymas. kai a ≠ 1, a ≠ ± 2; x - bet kuris realusis skaičius, kai a = 1. sprendinių nėra, kai a = ± 2.

f)(2 a³ - a² - 2 a + 1)x = (2 a -1)(a +1); Pertvarkome lygtį: (2 a -1)(a +1)x = (2 a -1)(a +1); 1) Kai a ≠ 0, 5; a ≠ ± 1, tai 2) Kai a = 0, 5, tai 0·x = 0 ir sprendiniai visi skaičiai; 3) Kai a =1, tai 0·x = 2 ir lygtis sprendinių neturi; 4) Kai a = -1, tai 0·x = 0 ir sprendiniai visi skaičiai. Atsakymas. kai a ≠ 0, 5; a ≠ ± 1 x - bet kuris realusis skaičius, kai a = 0, 5; a = -1; sprendinių nėra, kai a = 1.

77. Su kuriomis m reikšmėmis lygties sprendinių moduliai lygūs, o patys sprendiniai yra priešingų ženklų: a) x² + (3 m - 5)x – 4 = 0;

79. Su kuriomis parametro a reikšmėmis lygties sprendinių suma lygi jų sandaugai:

97. Išspręskite nelygybę: a) 5 x – a > ax + 3;