Typing Staphylococcus aureus using the protein A gene

Typing Staphylococcus aureus using the protein A gene Phaedra Agius – January, 2008, completed at RPI in New York in collaboration with Barry Kreiswirth, Steve Naidich, Kristin Bennett

Introduction • • • What is staph? Typing methods and the sp. A gene The data Comparing Sequences Similarities and differences Hierarchical clustering Evaluating the results Multidimensional Scaling Conclusion

• Staphylococcus aureus is a bacteria often living on the skin or in the nose of a healthy person. • It can spread rapidly • Some strains are resistant to antibiotics (MRSA) • Staph can cause a multitude of infections, from skin infections to more deadly infections such as pneumonia and meningitis

Typing Methods • Multi Locus Sequence Typing (MLST) is a well established typing method that looks at 7 house-keeping genes in staph. These are genes that are always turned on. • Our method looks at just ONE gene – the sp. A gene.

The sp. A gene • The sp. A gene contains information for making Protein A. • The protein A in staph is a virulence factor. It inhibits white blood cells from ingesting and destroying the bacteria by acting as an immunological disguise.

Preprocessed DNA sequences of the sp. A gene AAA GAG GAAGACAACAACAAGCCTGGT AAA GAAGATGGCAACAAGCCTGGT AAA GAAGACAACAAAAAACCTGGC AAA GAAGATGGCAACAAACCTGGT AAA GAAGACGGCAACAAGCCTGGT AAA GAAGATGGCAACAAGCCTGGT X 1 K 1 A 1 O 1 M 1 Q 1 The sp. A DNA sequences can be preprocessed into a sequence of repeats, or cassettes. Instead of dealing with the long DNA sequences, we use these shorter preprocessed spa sequences X 1 -K 1 -A 1 -O 1 -M 1 -Q 1 Note, first cassette has 27 bp, the others have 24 bp

Labeled data • 194 sequences labeled with their MLST type • The MLST allelic profile is provided for each sequence Spa sequences MLST labels

Comparing spa sequences • T 1 -J 1 -M 1 -G 1 -M 1 -K 1 • T 1 -K 1 -B 1 -M 1 -D 1 -M 1 -G 1 -M 1 -K 1 • T 1 -M 1 -D 1 -M 1 -G 1 -M 1 -K 1 • U 1 -J 1 -F 1 -K 1 -P 1 -E 1 • T 1 -J 1 -F 1 -K 1 -B 1 -P 1 -E 1 • U 1 -J 1 -G 1 -F 1 -M 1 -B 1 These ‘preprocessed’ sequences are highly conserved. How can we generate numbers from sequences that reflect the subtle differences and/or similarities between them?

Comparing spa sequences – Global alignment – Affine alignment – BCGS - Best common gap-weighted subsequence • Weighting the sequence ends (B and E) Using these methods each spa sequence can be represented as a vector of similarity scores between itself and all the other sequences

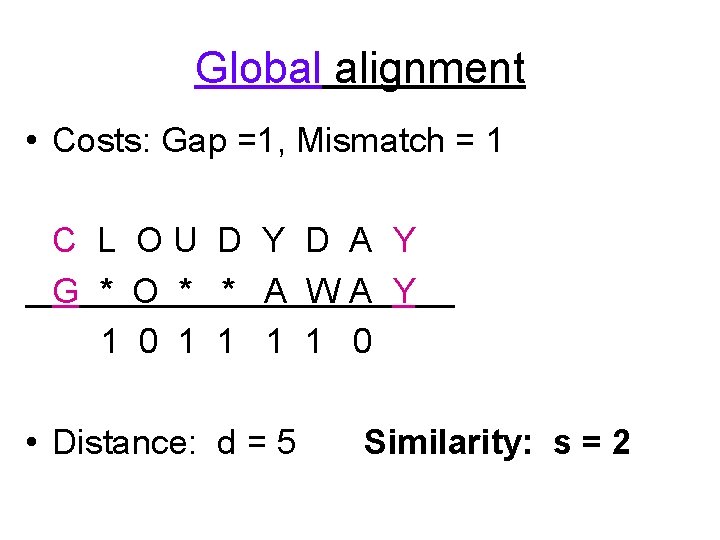
Global alignment • Costs: Gap =1, Mismatch = 1 C L OU D Y D A Y G * O * * A WA Y 1 0 1 1 0 • Distance: d = 5 Similarity: s = 2

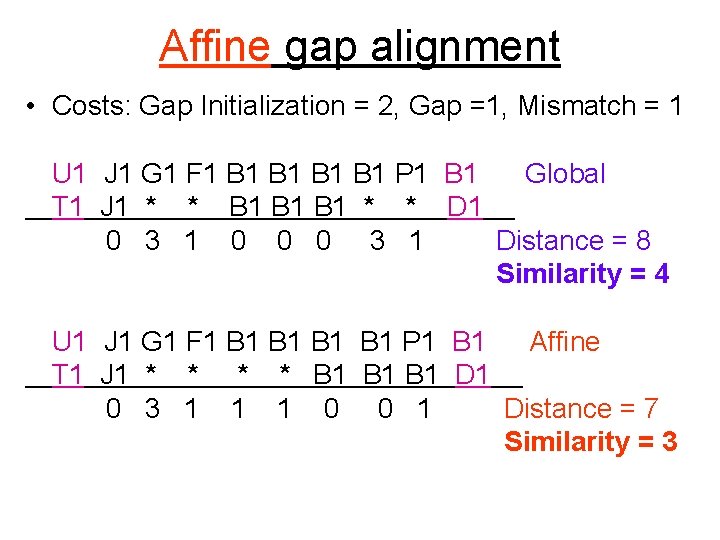
Affine gap alignment • Costs: Gap Initialization = 2, Gap =1, Mismatch = 1 U 1 J 1 G 1 F 1 B 1 B 1 P 1 B 1 Global T 1 J 1 * * B 1 B 1 * * D 1 0 3 1 0 0 0 3 1 Distance = 8 Similarity = 4 U 1 J 1 G 1 F 1 B 1 B 1 P 1 B 1 Affine T 1 J 1 * * B 1 B 1 D 1 0 3 1 1 1 0 0 1 Distance = 7 Similarity = 3

BCGS-Best Common Gap-weighted Subsequence P ARTYHAR D P ANT * * *R Y Common subsequences are: S 1 = A, T , R, S 2 = AT , S 3 = T R, S 4 = AT R Gap weighted scores: Choose a weight 0< =<ג 1 S 1 = 1¸ 0 = 1, S 2 = 2¸ , S 3 = 2¸ 3 , S 4 = 3¸ 4

S 1 = A, T , R, S 2 = AT , S 3 = T R, S 4 = AT R S 1 = 1¸ 0 = 1, S 2 = 2¸ , S 3 = 2¸ 3 , S 4 = 3¸ 4 If =ג 1, then S 4 is the optimal choice. If =ג 0. 9, the scores are 1, 1. 8, 1. 46 and 1. 97 respectively If =ג 0. 8, the scores are 1, 1. 6, 1. 02 and 1. 23 respectively

Normalizing the similarity scores • The similarity scores follows: M are normalized as where n 1 and n 2 are the sequence lengths Example: L OU D Y D A Y G * O * * A WA Y C Similarity = 3, Normalized similarity = 3/√(7*4)=0. 57

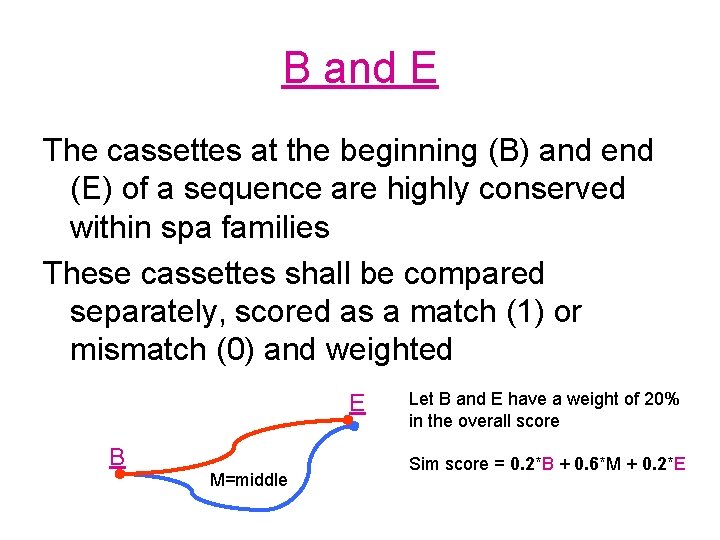
B and E The cassettes at the beginning (B) and end (E) of a sequence are highly conserved within spa families These cassettes shall be compared separately, scored as a match (1) or mismatch (0) and weighted E B M=middle Let B and E have a weight of 20% in the overall score Sim score = 0. 2*B + 0. 6*M + 0. 2*E

Similarities Distances Normalized similarity scores can be transformed to distances as follows: D (s 1 ; s 2 ) = 1 ¡ si m(s 1 ; s 2 ) Spa sequence vector of distances between that sequence and every other sequence in the dataset. The set of spa sequences is now represented by a (normalized) distance matrix.

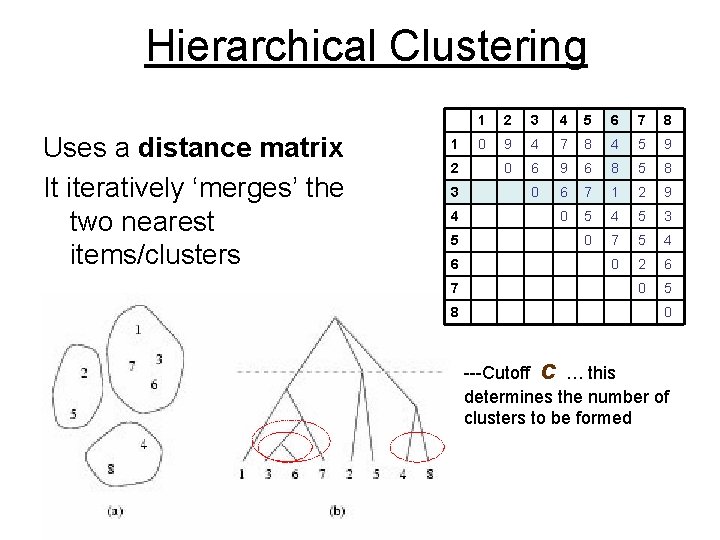
Hierarchical Clustering Uses a distance matrix It iteratively ‘merges’ the two nearest items/clusters 1 2 3 4 5 6 7 8 0 9 4 7 8 4 5 9 0 6 9 6 8 5 8 0 6 7 1 2 9 0 5 4 5 3 0 7 5 4 0 2 6 0 5 0 ---Cutoff c … this determines the number of clusters to be formed

Training and Testing Test Train • Split the data into two – a TRAINING set and a TEST set • Build a model on the Training set by choosing optimal B, E and c parameters • Assign the Test data to the nearest clusters • Evaluate the results • Repeat multiple times for validation

Assigning Test sequences to the Training clusters • We define the distance between a point and a cluster to be the mean of the distances between that point and the members of the cluster. >t IF the distance between a test point and the nearest cluster exceeds an outlier threshold t , the test point is defined to be an outlier (a novel strain of the bacteria) ELSE the test point is assigned to the nearest cluster.

Evaluation • Compare our clusters to the groups defined by the MLST labels via the Jaccard coefficient • Split our data into a Training and Testing set multiple times and measure the consistency of the clusters formed via a Stability score • Measure the Accuracy of our spa groups by comparing them to the MLST groups

Jaccard coefficient Clustering S Clustering M

Stability The stability is measured over the n Training and Testing iterations. It is defined to be the mean of the Jaccard scores measured pairwise between the spa clusterings obtained at each iteration Iterations 1, 2, 3 …. J 1 Spa clustering 1 J 3 Spa clustering 2 J 2 Spa clustering 3 Stability = mean(J 1, J 2, J 3)

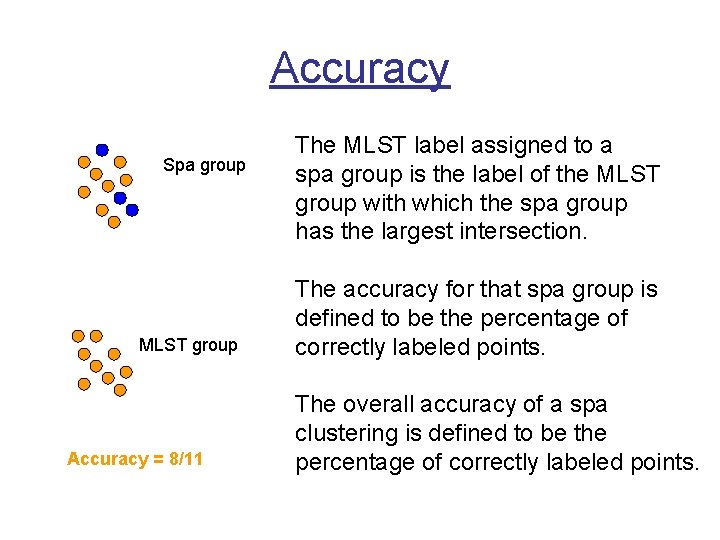
Accuracy Spa group MLST group Accuracy = 8/11 The MLST label assigned to a spa group is the label of the MLST group with which the spa group has the largest intersection. The accuracy for that spa group is defined to be the percentage of correctly labeled points. The overall accuracy of a spa clustering is defined to be the percentage of correctly labeled points.

Results: Jaccard scores (40 iters, outlier threshold = 1. 5 sd)

Results: Stability scores (40 iters, outlier threshold = 1. 5 sd)

Results: Accuracy scores (40 iters, outlier threshold = 1. 5 sd)

Results: Outlier detection (40 iters, outlier threshold = 1. 5 sd)

Results: Varying the Outlier threshold (10 iters, test set size = 30%)

Multidimensional Scaling (MDS) • MDS translates a distances matrix to a set of coordinates such that the distances between the points are approximately equal to the dissimilarities. Picture taken from Forrest W. Young’s paper ‘Multidimensional Scaling’

MDS with our distances

MDS – a closer look

Conclusion and future work • The Spa clustering method can refine groups in ways that MLST cannot • BCGS worked best • MDS on our spa distances clearly draws out the clusters Future research • More data, compare to other typing methods • Use BCGS on other data types • Different distance measures • Different ways of assigning test points to clusters • Better ways for finding the optimal parameters other than a grid search

References • • • Spa Typing method for Discriminating among Staphylococcus aureus Isolates: Implications for Use of a Single marker to Detect Genetic Micro and Macrovariation Larry koreen, Srinivas Ramaswamy, Edward Graviss, Steven Naidich, James Musser and Barry Kreiswirth Evaluation of protein A Gene Polymorphic Region DNA Sequencing for Typing of Staphylococcus aureus Strains B. Shopsin, M. Gomes, S. O. Montgomery, D. H. Smith, M. Waddington, D. E. Dodge, D. A. Bost, M. Riehman, S. Naidich and B. Kreiswirth Introduction to Computational molecular Biology Joao Setubal and Joao Meidanis Kernel Methods for Pattern Analysis John Shawe-Taylor and Nello Cristianini Framework for kernel regularization with application to protein clustering Fan Lu, Sunduz Keles, Stephen J. Wright and Grace Wahba

Thanks! Questions? This work is published in IEEE/ACM Transactions on Computational Biology and Bioinformatics Volume 4, Issue 4, Oct. -Dec. 2007 Page(s): 693 - 704