Types of Statistics Descriptive Statistics e g frequencies

Types of Statistics • Descriptive Statistics • e. g. , frequencies, percentiles, mean, median, mode, ranges, inter-quartile ranges, sds, Zs • Describe data • Inferential Statistics • e. g. , t, ANOVA (F), correlations (r), regression weights (ß); variance explained (R 2) • Allow for inferences about population to be drawn from sample data

Descriptive Statistics • Frequencies, percentiles • Central Tendency • Mean • Sum of all observations divided by total number of observations • Median • After arraying all observations in ascending/descending order, the obs that divides the sample into two • For even number of observations take avg of 2 central obs • Mode • Most frequently occurring observation • When would one use means vs. medians? p. 396 Sekaran (Economist article)

Descriptive Statistics • Variability • Range • Difference between the two most extreme observations • Inter-quartile range • Divide observations into quarters & use the middle half • Standard Deviation • Take each observation’s difference from the mean, square it, add all such squared differences, and divide the result by number of observations • Variance • Square of standard deviation p. 397 Sekaran

Descriptive Statistics • Variability (cont’d) • Confidence intervals • The range of values in which the mean occurs 95% of the time • Typically includes scores that are two standard errors above or below statistic » Standard error: Type of standard deviation (for more see p. 287 Sekaran) • Standard scores (Zs) • Deviation from the mean divided by standard deviation • Mean of all Zs =0, sd=1 • Useful for computing interaction scores in regression analyses

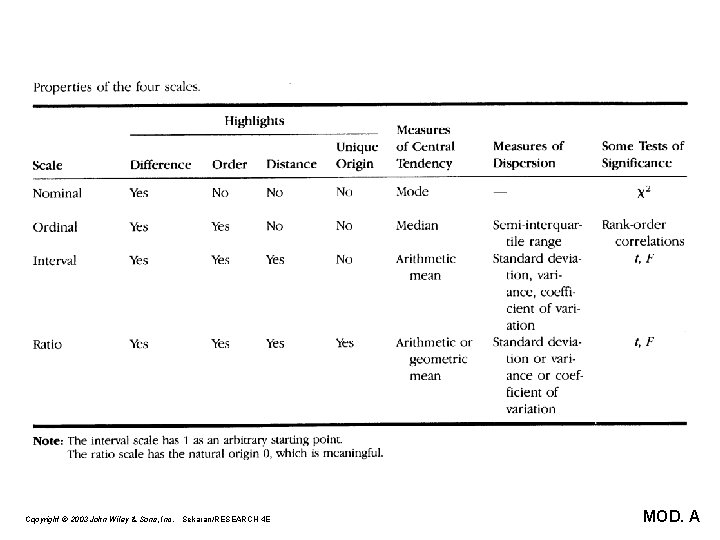
Types of Variables • Categorical • Nominal; Ordinal • Can compute frequencies & mode for nominal • For ordinal variables, carefully interpret descriptive statistics • Continuous • Interval; Ratio • Can compute descriptive statistics

Copyright © 2003 John Wiley & Sons, Inc. Sekaran/RESEARCH 4 E MOD. A

Types of Inferential Statistics • Parametric vs. non-parametric statistics • Non-parametric does not assume normal distribution of data • T-test • ANOVA (F) • Correlations (r) • Types of • Multiple-regression (R) • Regression weights (ß); Variance explained (R 2) p. 394 Sekaran

Key Assumptions • Behavioral research explains individual differences in psychological variables • Good measures of psychological variables capture individual differences • Individual differences in psychological variables are normally distributed • Some psychological variables can be ‘transformed’ to be normally distributed • Variables with normal distributions have interval properties & allow for computation of commonly used inferential statistics

Inferential Statistics See also p. 405 Sekaran

Tests of Mean Differences • T-test • Compares whether means of two groups are different from each other 95% of the time • Compares differences on one independent variable • Paired t-test= Same group, two different times or measurements • Can be used as a post-hoc or planned contrast after conducting ANOVA analyses • Beware the number of t-tests done reduces confidence level so use Scheffe’s, Duncan multiple range etc.

Tests of Mean Differences • ANOVA (F-test) • Compares whether means of three or more groups are different from each other 95% of the time • Compares two or more independent variables • Tests interaction effects: Does the effect of one IV depend on the level of the other IV? • Repeated measures ANOVA: Same sample, multiple times/measurements • Sparingly conduct T-test to see if pairs of groups are significantly different from each other

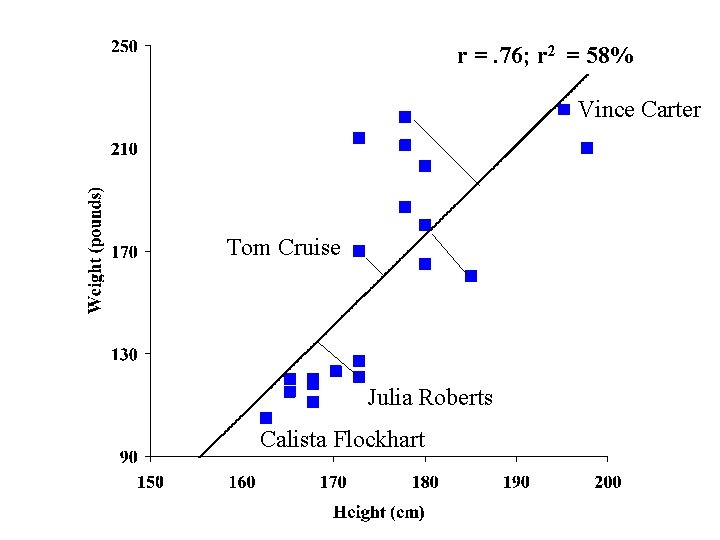
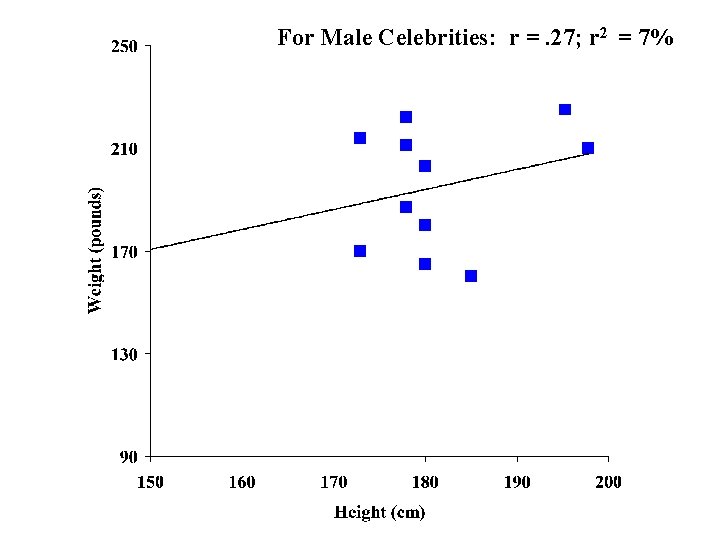
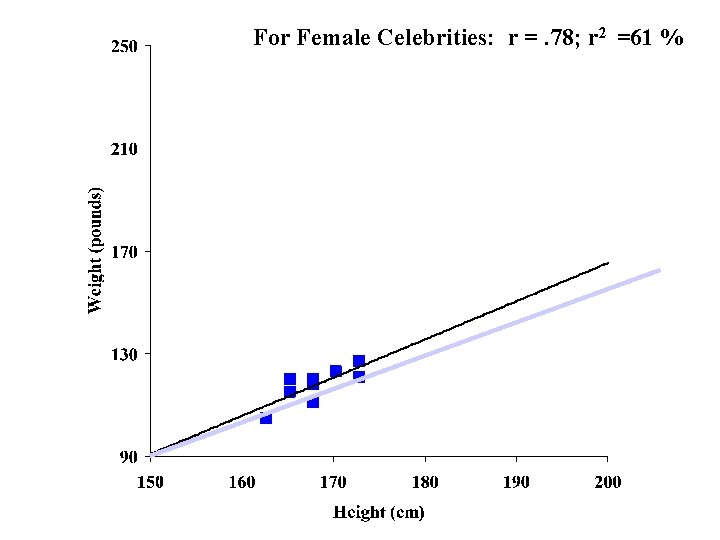
Tests of Association • Correlation coefficient (r) • Assesses whether 2 variables are ‘linearly’ related to each other 95% of the time • Reflects the direction and the strength of the relation • Varies from – 1 to +1. • Better measure of the strength of a relation is the amount of explained variance (r 2) • Ranges from 0 to 100 • Difference between r=. 3 & r=. 4 is not the same as difference between r=. 7 & r=. 8

Tests of Association • Types of Correlations • When both variables are continuous: Pearson product-moment • When both variables are nominal (categorical) • Two categories for each variable: Phi • Multiple categories for each variable: Kappa • When both variables are ordinal: Spearman rank • Significance of r = t-test

r =. 76; r 2 = 58% Vince Carter Tom Cruise Julia Roberts Calista Flockhart

For Male Celebrities: r =. 27; r 2 = 7%

For Female Celebrities: r =. 78; r 2 =61 %

Tests of Association • Multiple correlation (R) • Describe relation between 3 or more variables (e. g. , 2 predictors and one criterion) • Two different formulae depending on whether or not predictors are correlated with each other • Tests non-linear relationships • Significance of R =F-test • Are variables related to each other 95% of the time? 405 -407 Sekaran

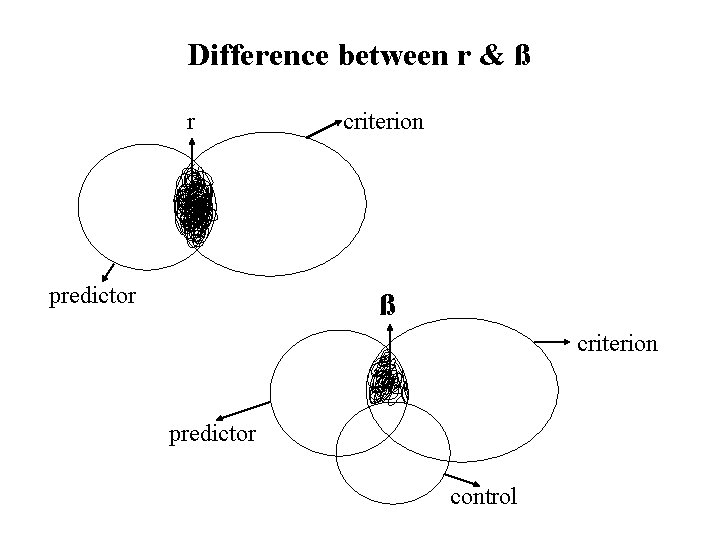
Difference between r & ß r predictor criterion ß criterion predictor control

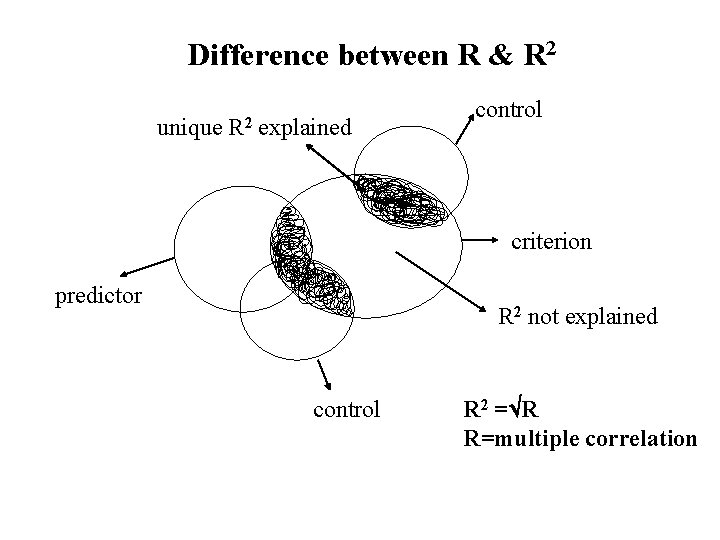
Difference between R & R 2 unique R 2 explained control criterion predictor R 2 not explained control R 2 = R R=multiple correlation

TITLE HERE