Types 2 Recursive Problems if this is a

Types (2)

Recursive Problems if this is a simple case solve it else redefine the problem using recursion o One or more simple cases of the problem have a straightforward, nonrecusive solution o The other cases can be redefined in terms of problems that are closer to the simple case o By applying this redefinition process every time the recursive function is called, eventually the problem is reduced entirely to simple csaes, which are relatively easy to solve. 2

Example int multiply (int m, int n) { int ans; if (n==1) ans = m; else ans = m + multiply ( m , n-1 ) return (ans); } 3

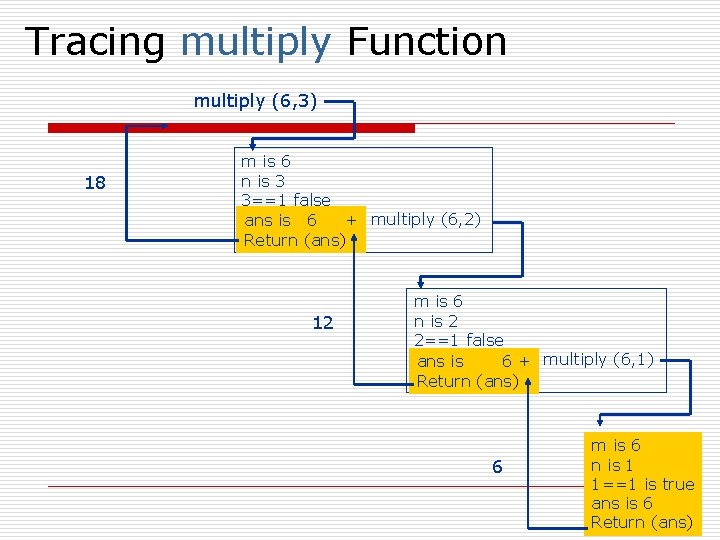
Tracing multiply Function multiply (6, 3) 18 m is 6 n is 3 3==1 false ans is 6 + multiply (6, 2) Return (ans) 12 m is 6 n is 2 2==1 false ans is 6 + multiply (6, 1) Return (ans) 6 m is 6 n is 1 1==1 is true ans is 6 4 Return (ans)

Recursive Data Type (1) o Recursive data type uses itself in its declaration o Recursive data types are important to recursive algorithms o Used to represent data whose size and structure is not known in advance o Examples: lists and trees 5

Recursive Data Type (2) Struct Char. List { char data; Sturct Char. List next; /* illegal C*/ }; o Needs a unlimited storage space (illegal C) o In the analogy with recursive functions Int factorial (int n) { return n * factorial (n-1); } /* illegal C*/ o No base case (test to stop the recursion) 6

Recursive Data Type (3) o The solution: using pointers to allow manual dynamic allocation Struct Char. List. Node { char data; Sturct Char. List. Node *next; /* legal C*/ }; o Each individual element in a Char. List. Node has a fixed size o Elements can be linked together to form a list of arbitrary size 7

Type Equivalence o The assignment statement serves to replace the current value of a variable with a new value specified as an expression. n The variable (or the function) and the expression must be of identical type. o Name Equivalence n Two types are equivalent if they have the same name o Structure Equivalence n Two types are equivalent if they have the same structure 8

struct complex { float re, im; Example: o Name equivalent n n c and d have the same type a and c haven’t the same type o Structure equivalent n n a, b, c, d have the same type d and e haven’t the same type o Field names are different }; struct polar { float x, y; }; struct y { float re, im; }; struct complex c, d; Struct y a, b; struct polar e; int f[5], g[10]; 9

Subtypes o A subtype is a type that has certain constraints placed on its values or operations. 10

Ada Example subtype one_to_ten is Integer range 1. . 10; type Day is (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday); subtype Weekend is Day range Saturday. . Sunday; type Salary is delta 0. 01 digits 9 range 0. 00. . 9_999. 99; subtype Author_Salary is Salary digits 5 range 0. 0. . 999. 99; 11

Java example o An object s of class S can be assigned to object t of class T ot=s n n Either S and T are the same class Or S is a subclass of T Widening Conversion 12

Polymorphism and Generics (1) o Polymorphism Comes from Greek n Means: having many forms o A function or operation is polymorphic if it can be applied to any one of several related types and achieve the same result o Operators overloading is a kind of polymorphism o An advantage of polymorphism is that it enables code reuse. 13

Polymorphism and Generics (2) o To enables code reuse Ada introduced the concept of generics or template o A generic function is a template that can be instantiated at a compile time with concrete types and operators n Binding of arguments to a type is deferred from programming time to compile time. 14

Polymorphism and Generics (3) o C++ provides generics or templates o The implementation mechanism n Actual parameters are textually substituted for generic parameters n Resulting text is then compiled 15