Typed Lambda Calculus Adapted from Lectures by Profs

Typed Lambda Calculus Adapted from Lectures by Profs Aiken and Necula of Univ. of California at Berkeley CS 776 Prasad 1

Lecture Outline • Lambda Calculus – Review and examples • Simple types • Type checking • Comparison with OO type systems CS 776 Prasad 2

Lambda Calculus Review • Grammar: E : : = x | E 1 E 2 | lx. E • variables function application function creation Evaluation: (lx. e) e’ ® [e’/x]e CS 776 Prasad 3

Example 1 (lx. x) ly. y ® ly. y (lx. x) ly. y ® [ly. y/x] x = ly. y CS 776 Prasad 4

Example 2 (lx. ly. x) (lz. z) e ®* lz. z ((lx. ly. x) (lz. z)) e ® ([lz. z/x]ly. x) e = (ly. lz. z) e ® [e/y]lz. z = lz. z CS 776 Prasad 5

Example 3 (lx. x x) ®. . . (lx. x x) ® [(l x. x x)/x](x x) = (lx. x x) CS 776 Prasad 6

Question What programming errors can occur in lambda calculus? CS 776 Prasad 7

Notes • We can encode anything we like in lambda calculus – Booleans, integers, objects, if-then-else, recursion, . . . • But don’t forget that these are encodings – Akin to programming directly with 0’s and 1’s CS 776 Prasad 8

Extension • Grammar: E : : = x | E 1 E 2 | lx. E | 0, 1, 2, … | + • variables function application function creation integers addition Evaluation: (lx. e) e’ ® [e’/x]e +ij®k CS 776 where k = i + j Prasad 9

Digression • There is nothing magic about adding integers and + as constants to the lambda calculus • We could add any data types and operations we like • They can be encoded directly in lambda calculus anyway CS 776 Prasad 10

Examples (lx. + x 1) (lx. + x x) (lx. + x 1) 3 ® 4 (lx. + x 1) (ly. y) ® ? CS 776 Prasad 11

What Happens? (lx. + x 1) (ly. y) ® + (ly. y) 1 ® ? Answer: It depends. A runtime error; we can’t add to a function Or no error: If + and 1 are encoded as lambda terms, computation will continue! CS 776 Prasad 12

Notes • Assume 1, + are encoded as lambda terms • Nothing guarantees the encoding of 1 is used as an integer – E. g. , (1 lx. x) – Evaluation doesn’t know what the encodings are supposed to represent CS 776 Prasad 13

Back to the Future • We need to be able to restrict uses of values to appropriate operations • We need a type system! • Note that we’d like a type system whether or not + (ly. y) 1 causes a runtime error – Catching these errors before program execution is better CS 776 Prasad 14

Typed Lambda Calculus • Grammar: E : : = x | E 1 E 2 | lx: t. E | 0, 1, 2, … | + • variables function application function creation integers addition Evaluation: (lx: t. e) e’ ® [e’/x]e +ij®k CS 776 where k = i + j Prasad 15

The Types • We have only two kinds of values – Integers – Functions • Type grammar: t : = int | t ® t CS 776 Prasad 16

Examples of Types int ® int (int ® int) ® int ® (int ® int) CS 776 Prasad 17

Type Judgments “it is provable that” “has type” Type environment Type Expression CS 776 Prasad 18

Examples CS 776 Prasad 19

More Examples CS 776 Prasad 20

Type Rule: Variables [Var] A variable has the type assumed in the type environment. CS 776 Prasad 21

Abstraction [Abs] A function has type t 1 ® t 2 if the function body has type t 2 when we assume the argument has type t 1. CS 776 Prasad 22

Application [App] Applying a function of type t 1 ® t 2 to an argument of type t 1 gives a result of type t 2 CS 776 Prasad 23

Integers [Int] An integer has type int CS 776 Prasad 24

Addition [Add] Adding two int’s produces an int CS 776 Prasad 25

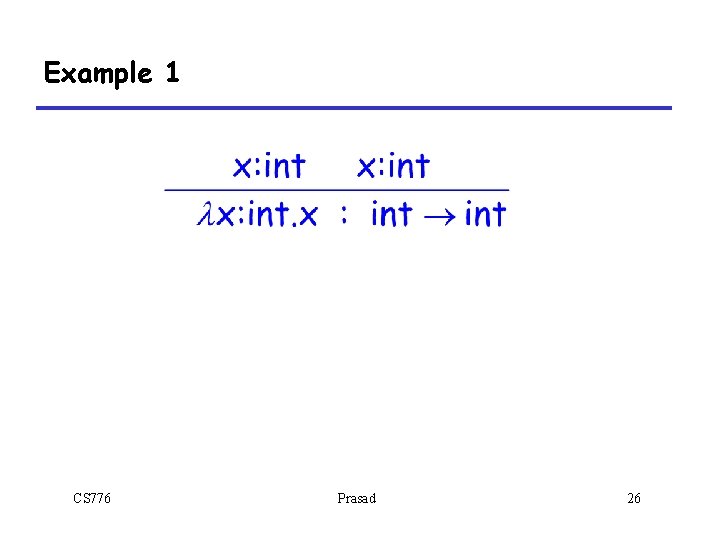
Example 1 CS 776 Prasad 26

Example 2 CS 776 Prasad 27

Type Checking • One recursive descent traversal. • Top-down: Add type declarations of formal parameters to environments [Abs] CS 776 Prasad 28

Type Checking (Cont. ) • Bottom-up: Check that types match in applications [App] CS 776 Prasad 29

Structural Equality • “Types match” means “types are equal” • Equality is recursively defined int = int a®b=c®d Û CS 776 Prasad a=cÙb=d 30

Notes • In typed lambda calculus: – Types of all variables are declared – Types are structured (e. g. , int ® int) – Types are checked for equality • Many typed languages in this class – Nearly all typed languages before 1980 – FORTRAN, ALGOL, Pascal, C – Captures C typing except for casts & coercions CS 776 Prasad 31

Typed OO Languages • In many typed object-oriented languages – Types of all variables are declared – Types are non-structural (just names) • Declare all types and type relationships – Types are checked for subtyping relationships • What if type declarations are omitted? – A language with type inference CS 776 Prasad 32

Discussion What about structural types + subtyping? – Area of current research – Currently no consensus on the right way to combine C-like type systems with typical OO-like type systems CS 776 Prasad 33