TYPE TABLEAU PARTIE 2 MATRICES Introduction Dfinition de

TYPE TABLEAU PARTIE 2 : MATRICES - Introduction - Définition de la structure de tableau - Tableau à une dimensions (Vecteurs) - Problèmes à résoudre sur les vecteurs. - Tableau à deux dimension (Matrices) - Problèmes à résoudre sur les matrices. Réalisé par : OUZEGGANE Redouane Département de Technologie Faculté de Technologie – Université A. Mira, Bejaia Année Universitaire 2015/2016

TYPE TABLEAU : VECTEUR & MATRICE Tableaux à 1 dimension (Vecteurs) Pour traiter les problèmes nécessitant une représentation vectorielle des données. Tableaux à 2 dimensions (Matrices) Problèmes nécessitant une représentation matricielle des données. 1ère Année Technologie 01/08 Année Universitaire : 2015/2016

TABLEAUX À DEUX DIMENSIONS - MATRICE Syntaxe & Sémantique Déclaration <id_variable> : Tableau [<ii. L>. . <if. L>, <ii. C>. . <if. C>] de <type>; <ii. L>. . <if. L> : Plage d’indices des lignes <ii. C>. . <if. C> : Plage d’indices des colonnes ii. L : indice initiale des lignes ii. C : indice initiale des colonnes if. L : indice final des lignes if. C : indice final des colonnes <id_variable> : Array [<ii. L>. . <if. L>, <ii. C>. . <if. C>] of <type>; - Pour simplifier : ii. L et ii. C valent toujours 1 - Si ii. L=1, donc if. L est le nombre maximal de lignes. - Si ii. C=1, donc if. C est le nombre maximal de colonnes. 1ère Année Technologie 02/08 Année Universitaire : 2015/2016

TABLEAUX À DEUX DIMENSIONS - MATRICE Syntaxe & Sémantique Déclaration : Exemple A : Tableau [1. . 10, 1. . 10] de Réel; N, M : entier; T : Array [1. . 10, 1. . 10] of Real; N, M : integer; Remarques : 1 - Ci-dessous, déclaration d’une matrice de taille maximale 10 lignes et 10 colonnes. 2 - Pour donner la main à l’utilisateur de saisir la taille de la matrice qu’il veut utiliser, nous ajoutons deux variables entières N, M : N nombre de lignes et M nombre de colonnes. 1ère Année Technologie 03/08 Année Universitaire : 2015/2016

TABLEAUX À DEUX DIMENSIONS - MATRICE Syntaxe & Sémantique Lecture Pour parcourir les linges Lire(N, M); pour i 1 à N faire pour j 1 à M faire Lire( A[i, j] ) fin-pour Pour parcourir les colonnes Read(N, M); for i : = 1 to N do for j : = 1 to M do Read( T[i] ); La case de la matrice A dont N° ligne = i et N° de colonne = j Remarque : Les variable i et j, sert comme indices pour accéder à l’élément de la matrice situé à la ligne N° i et la colonne N° j. 1ère Année Technologie 04/08 Année Universitaire : 2015/2016

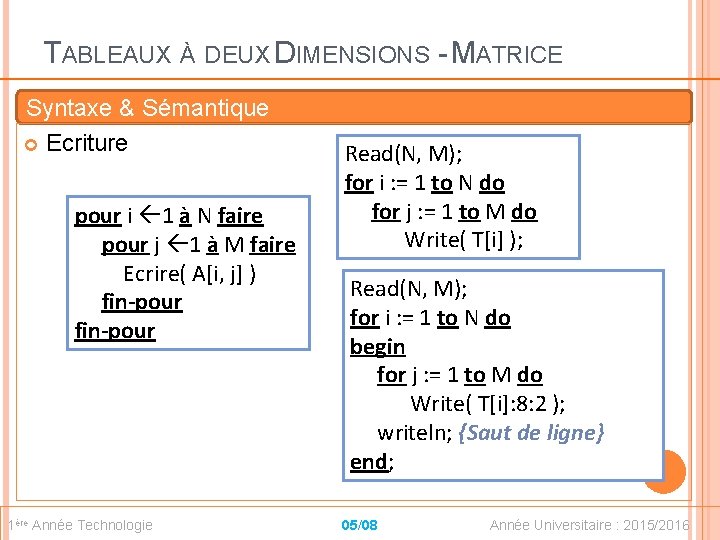
TABLEAUX À DEUX DIMENSIONS - MATRICE Syntaxe & Sémantique Ecriture pour i 1 à N faire pour j 1 à M faire Ecrire( A[i, j] ) fin-pour 1ère Année Technologie Read(N, M); for i : = 1 to N do for j : = 1 to M do Write( T[i] ); Read(N, M); for i : = 1 to N do begin for j : = 1 to M do Write( T[i]: 8: 2 ); writeln; {Saut de ligne} end; 05/08 Année Universitaire : 2015/2016

TABLEAUX À DEUX DIMENSIONS - MATRICE Syntaxe & Sémantique Algorithme Vecteur_lec_ecr Variables T : Tableau [1. . 10, 1. . 10] de réel N, M, i, j : entier Début Lire(N, M) pour i 1 à N faire pour j 1 à M faire Lire ( T[i] ) fin-pour Program Vecteur_lec_ecr; Uses wincrt; Var T : Array[1. . 10, 1. . 10] of real; N, M, i, j : integer; Begin {Lecture du Vecteur T} Read(N, M); for i : = 1 to N do for j : = 1 to M do Read (A[i, j]); pour i 1 à N faire pour j 1 à M faire Ecrire( A[i, j] ) fin-pour Fin. {Affichage du Vecteur T} for i : = 1 to N do for j : = 1 to M do Write (A[i, j]); End. 1ère Année Technologie 06/08 Année Universitaire : 2015/2016

TABLEAUX À DEUX DIMENSIONS - MATRICE Problèmes sur les matrices Somme et la moyenne des élément d’une matrices Somme et la moyenne de chaque lignes et/ou de chaque colonne Somme et Moyenne de la ligne N° k (ou de la colonne N° k) La recherche de l’élément minimum (et/ou maximum) dans une matrice et leurs positions (leurs indices de ligne et de colonne). Tri d’une matrice (Ordre croissant ou décroissant) La recherche d’une valeur dans une matrice La somme et le produit de deux matrices réelles. Ajouter une même valeur à tous les éléments d’une matrice Compter le nombre d’éléments (pairs, impaires, divisibles par …) …. . etc. 1ère Année Technologie 07/08 Année Universitaire : 2015/2016

DÉMONSTRATION Réaliser un programme PASCAL pour la lecture et l’écriture d’une Matrice. Réaliser un programme PASCAL pour recher une valeur val dans une matrice A (dans le cas ou la valeur est trouvée, afficher sa position). 1ère Année Technologie 08/08 Année Universitaire : 2015/2016