Type Inference using Type Constraints Type Inference using























- Slides: 53

Type Inference using Type Constraints

Type Inference using Type Constraints o Applications of typing axioms / rules are replaced with type equations. o A 3 -stages algorithm. Given an expression, e: • Rename bound variables in e. • Assign type variables to all sub-expressions of e. • Construct type equations. • Solve the equations. Question 1: Typing the expression ((lambda (f 1 x 1)) sqrt 4) Exp: ((lambda ([f 1: [N->N]] [x 1: N]): N (f 1 x 1)) sqrt 4) STAGE-I: Rename bound variables STAGE-II: Assign type variables to all sub-exps ((lambda (f x)) sqrt 4) Expression ((lambda(f x)) sqrt 4) (lambda(f x) f x sqrt 4 Var T 0 T 1 T 2 Tf Tx Tsqrt Tnum 4

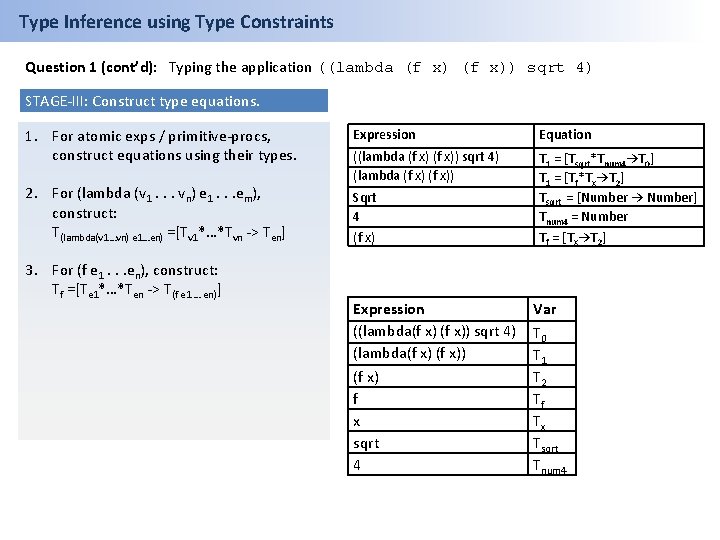
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Construct type equations. 1. For atomic exps / primitive-procs, construct equations using their types. Expression Equation 2. For (lambda (v 1. . . vn) e 1. . . em), construct: T(lambda(v 1…vn) e 1…en) =[Tv 1*…*Tvn -> Ten] ((lambda (f x)) sqrt 4) (lambda (f x)) Sqrt 4 (f x) T 1 = [Tsqrt*Tnum 4→T 0] T 1 = [Tf*Tx→T 2] Tsqrt = [Number → Number] Tnum 4 = Number Tf = [Tx→T 2] 3. For (f e 1. . . en), construct: Tf =[Te 1*…*Ten -> T(f e 1 … en)] Expression ((lambda(f x)) sqrt 4) (lambda(f x) f x sqrt 4 Var T 0 T 1 T 2 Tf Tx Tsqrt Tnum 4

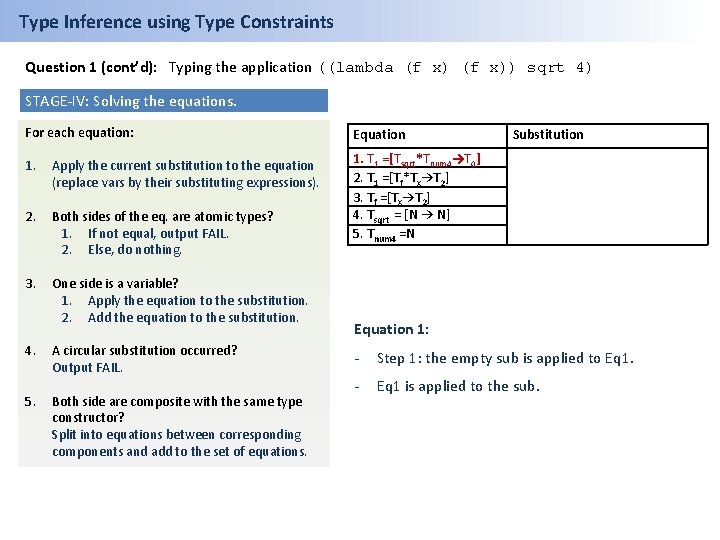
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 1. T 1 =[Tsqrt*Tnum 4→T 0] 2. T 1 =[Tf*Tx→T 2] 3. Tf =[Tx→T 2] 4. Tsqrt = [N → N] 5. Tnum 4 =N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Substitution Equation 1: - Step 1: the empty sub is applied to Eq 1. - Eq 1 is applied to the sub.

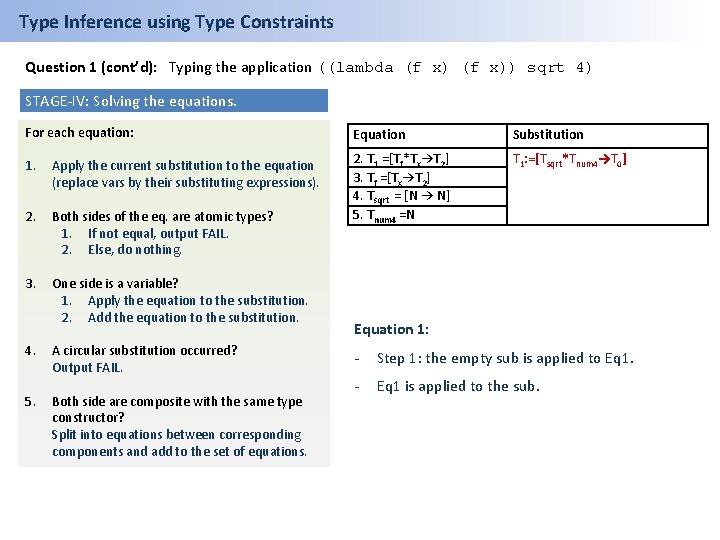
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tsqrt*Tnum 4→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 2. T 1 =[Tf*Tx→T 2] 3. Tf =[Tx→T 2] 4. Tsqrt = [N → N] 5. Tnum 4 =N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 1: - Step 1: the empty sub is applied to Eq 1. - Eq 1 is applied to the sub.

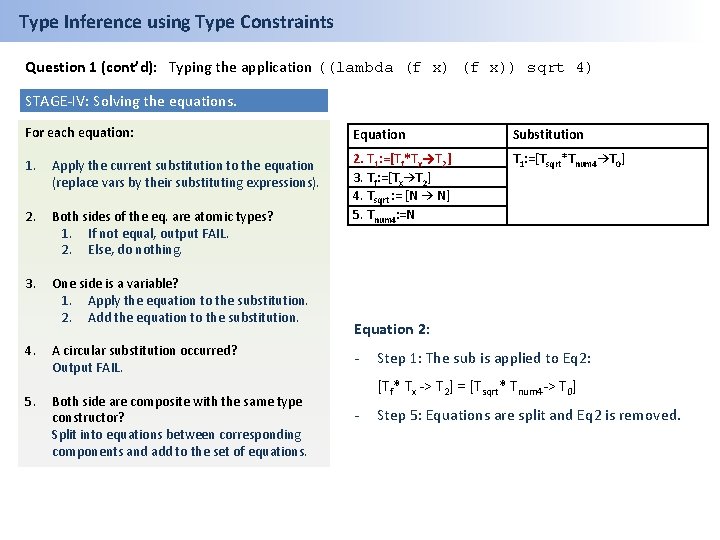
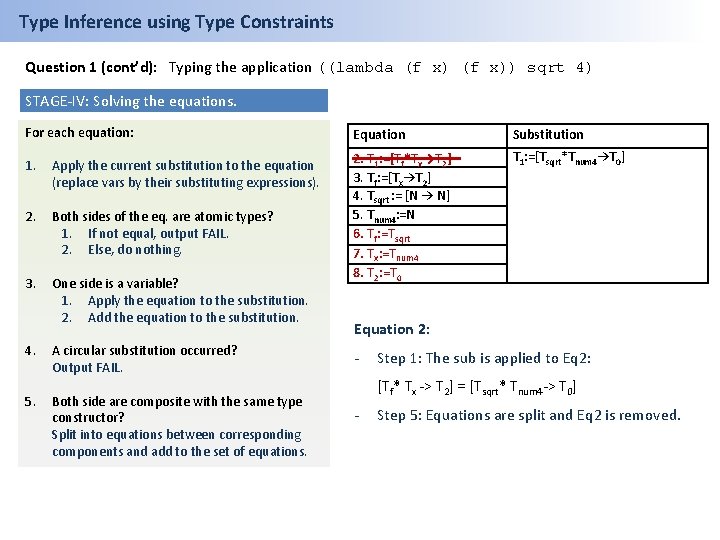
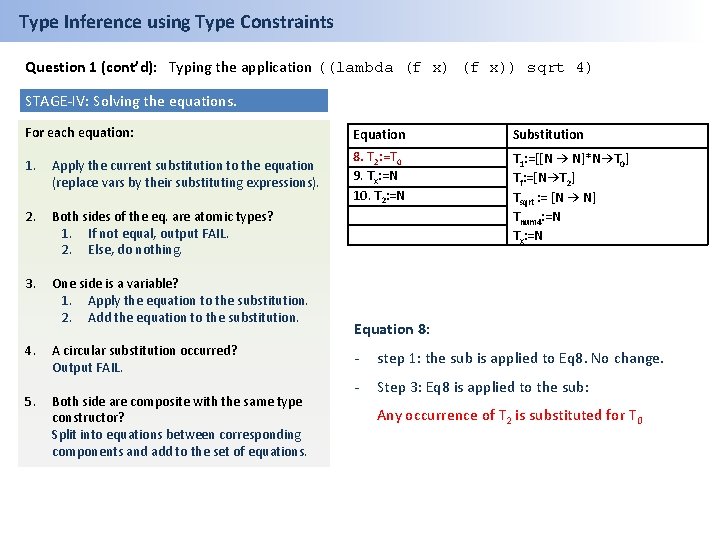
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tsqrt*Tnum 4→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 2. T 1: =[Tf*Tx→T 2] 3. Tf: =[Tx→T 2] 4. Tsqrt : = [N → N] 5. Tnum 4: =N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - Step 1: The sub is applied to Eq 2: [Tf* Tx -> T 2] = [Tsqrt* Tnum 4 -> T 0] - Step 5: Equations are split and Eq 2 is removed.

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tsqrt*Tnum 4→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 2. T 1: =[Tf*Tx→T 2] 3. Tf: =[Tx→T 2] 4. Tsqrt : = [N → N] 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - Step 1: The sub is applied to Eq 2: [Tf* Tx -> T 2] = [Tsqrt* Tnum 4 -> T 0] - Step 5: Equations are split and Eq 2 is removed.

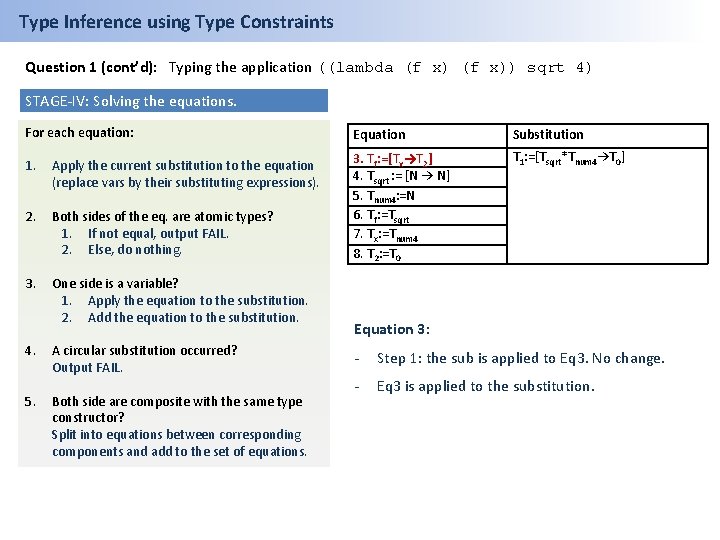
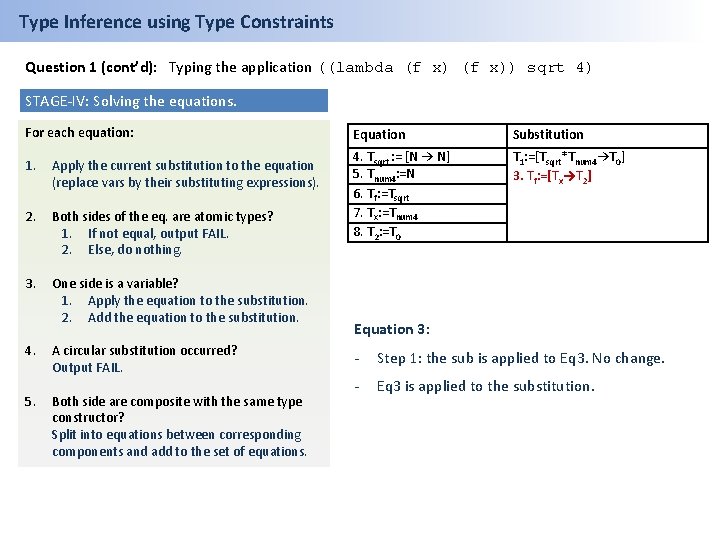
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tsqrt*Tnum 4→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. Tf: =[Tx→T 2] 4. Tsqrt : = [N → N] 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 3: - Step 1: the sub is applied to Eq 3. No change. - Eq 3 is applied to the substitution.

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 4. Tsqrt : = [N → N] 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[Tsqrt*Tnum 4→T 0] 3. Tf: =[Tx→T 2] Equation 3: - Step 1: the sub is applied to Eq 3. No change. - Eq 3 is applied to the substitution.

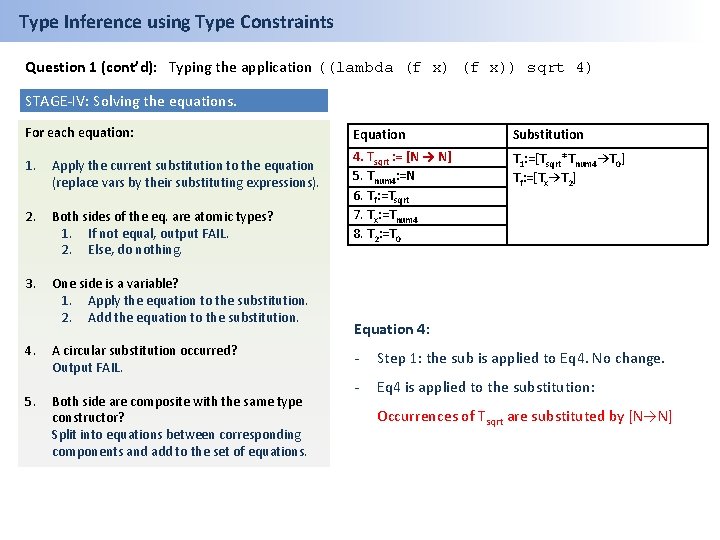
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 4. Tsqrt : = [N → N] 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[Tsqrt*Tnum 4→T 0] Tf: =[Tx→T 2] Equation 4: - Step 1: the sub is applied to Eq 4. No change. - Eq 4 is applied to the substitution: Occurrences of Tsqrt are substituted by [N→N]

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[[N → N]*Tnum 4→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Equation 4: - Step 1: the sub is applied to Eq 4. No change. - Eq 4 is applied to the substitution: Occurrences of Tsqrt are substituted by [N→N]

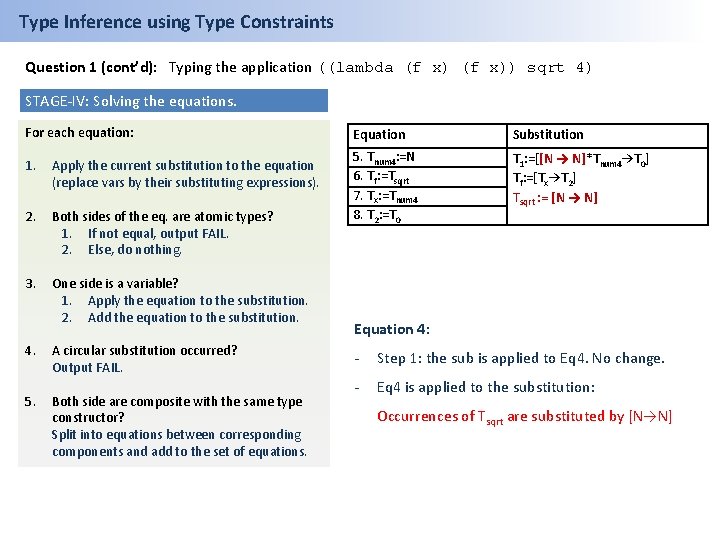
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 5. Tnum 4: =N 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[[N → N]*Tnum 4→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Equation 5: - Step 1: the sub is applied to Eq 5. No change. - Eq 5 is applied to the substitution: Occurrences of Tnum 4 are substituted by N

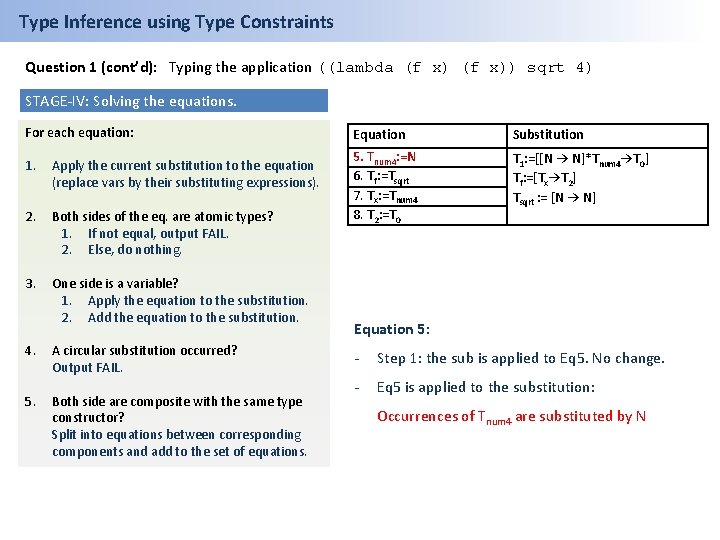
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[[N → N]*N→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Tnum 4: =N Equation 5: - Step 1: the sub is applied to Eq 5. No change. - Eq 5 is applied to the substitution: Occurrences of Tnum 4 are substituted by N

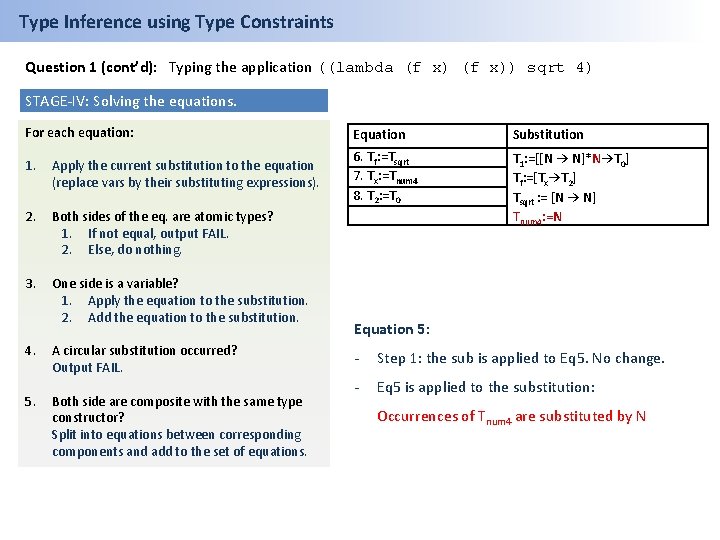
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 T 1: =[[N → N]*N→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Tnum 4: =N Equation 6: - Step 1: the sub is applied to Eq 6, Tf and Tsqrt are substituted: [Tx→T 2]=[N → N] - Step 5: Equations are split and Eq 6 is removed.

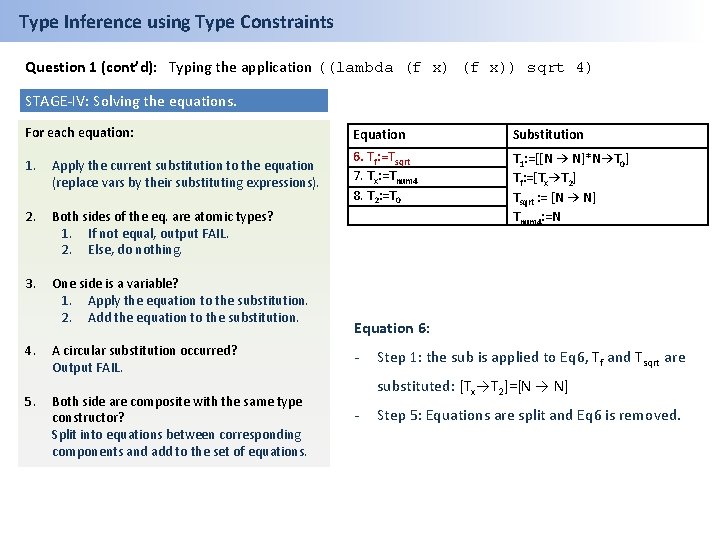
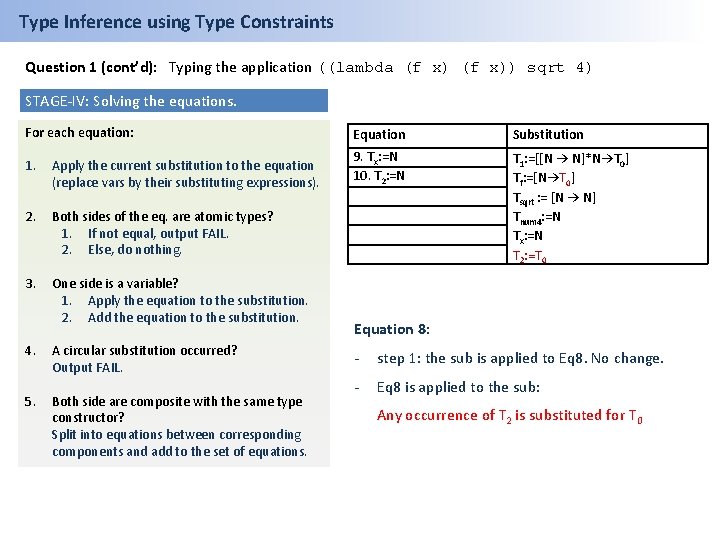
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 6. Tf: =Tsqrt 7. Tx: =Tnum 4 8. T 2: =T 0 9. Tx: =N 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Tnum 4: =N Equation 6: - Step 1: the sub is applied to Eq 6, Tf and Tsqrt are substituted: [Tx→T 2]=[N → N] - Step 5: Equations are split and Eq 6 is removed.

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 7. Tx: =Tnum 4 8. T 2: =T 0 9. Tx: =N 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Tnum 4: =N Equation 7: - Step 1: Tnum 4 is substituted: Tx=N - Step 3: Eq 7 is applied to the substitution: Any occurrence of Tx is substituted for N

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 7. Tx: =N 8. T 2: =T 0 9. Tx: =N 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[Tx→T 2] Tsqrt : = [N → N] Tnum 4: =N Equation 7: - Step 1: Tnum 4 is substituted: Tx=N - Step 3: Eq 7 is applied to the substitution: Any occurrence of Tx is substituted for N

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 8. T 2: =T 0 9. Tx: =N 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[N→T 2] Tsqrt : = [N → N] Tnum 4: =N Tx: =N Equation 7: - Step 1: Tnum 4 is substituted: Tx=N - Step 3: Eq 7 is applied to the substitution: Any occurrence of Tx is substituted for N

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 8. T 2: =T 0 9. Tx: =N 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[N→T 2] Tsqrt : = [N → N] Tnum 4: =N Tx: =N Equation 8: - step 1: the sub is applied to Eq 8. No change. - Step 3: Eq 8 is applied to the sub: Any occurrence of T 2 is substituted for T 0

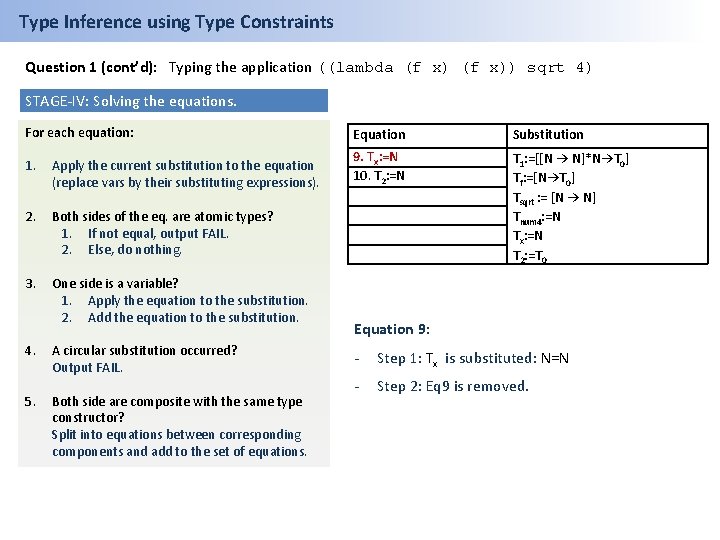
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 9. Tx: =N 10. T 2: =N 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. T 1: =[[N → N]*N→T 0] Tf: =[N→T 0] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =T 0 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 8: - step 1: the sub is applied to Eq 8. No change. - Eq 8 is applied to the sub: Any occurrence of T 2 is substituted for T 0

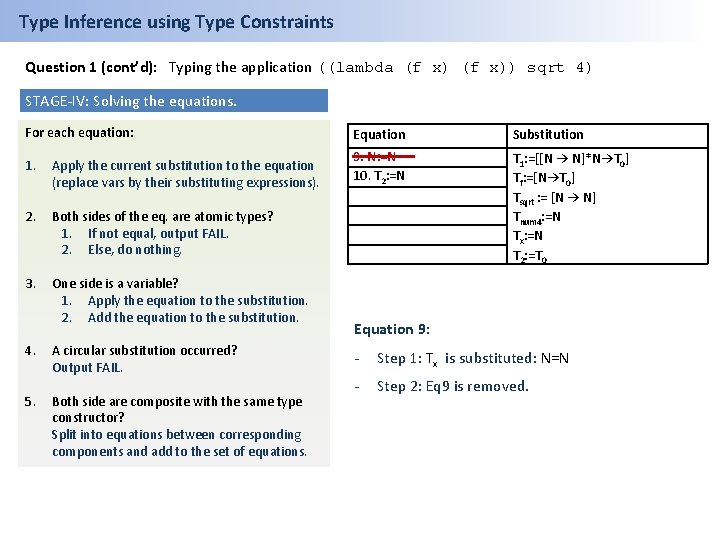
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 9. Tx: =N 10. T 2: =N 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. T 1: =[[N → N]*N→T 0] Tf: =[N→T 0] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =T 0 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 9: - Step 1: Tx is substituted: N=N - Step 2: Eq 9 is removed.

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 9. N: =N 10. T 2: =N 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. T 1: =[[N → N]*N→T 0] Tf: =[N→T 0] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =T 0 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 9: - Step 1: Tx is substituted: N=N - Step 2: Eq 9 is removed.

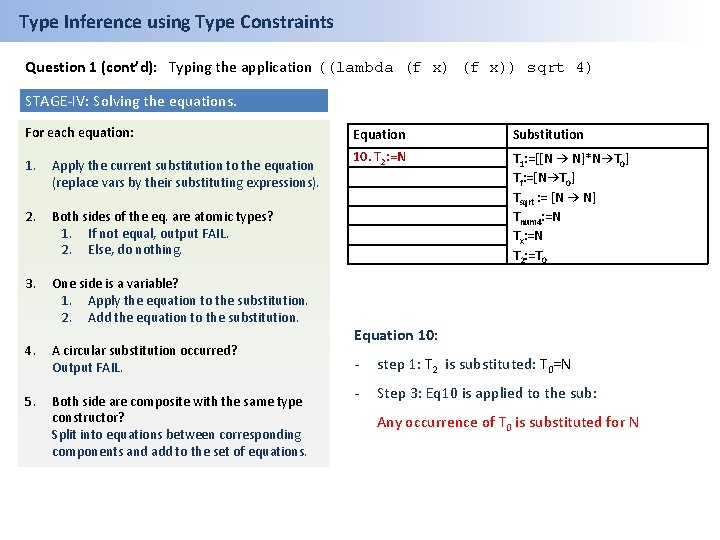
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 10. T 2: =N T 1: =[[N → N]*N→T 0] Tf: =[N→T 0] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =T 0 Equation 10: - step 1: T 2 is substituted: T 0=N - Step 3: Eq 10 is applied to the sub: Any occurrence of T 0 is substituted for N

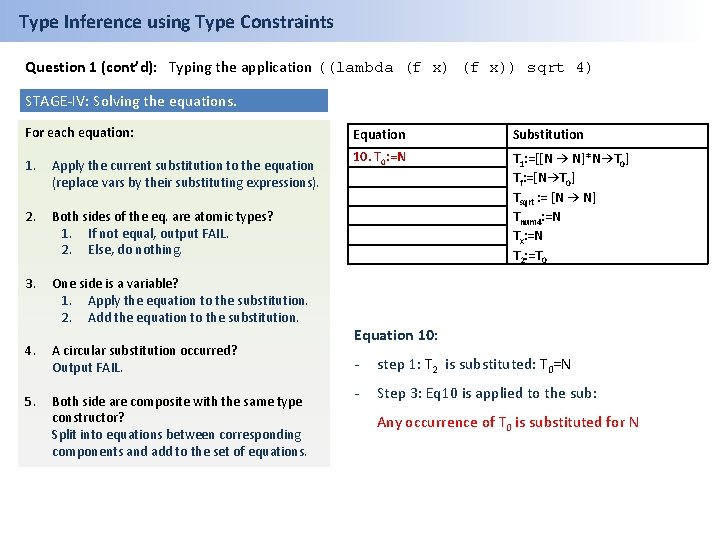
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 10. T 0: =N T 1: =[[N → N]*N→T 0] Tf: =[N→T 0] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =T 0 Equation 10: - step 1: T 2 is substituted: T 0=N - Step 3: Eq 10 is applied to the sub: Any occurrence of T 0 is substituted for N

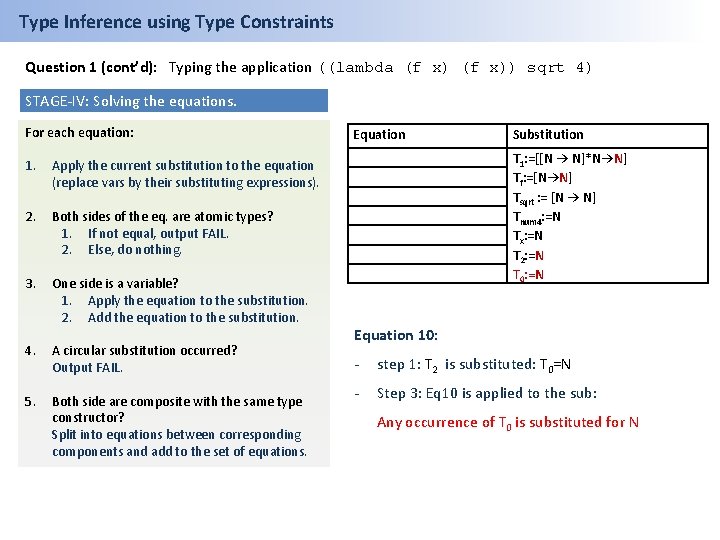
Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution T 1: =[[N → N]*N→N] Tf: =[N→N] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =N T 0: =N Equation 10: - step 1: T 2 is substituted: T 0=N - Step 3: Eq 10 is applied to the sub: Any occurrence of T 0 is substituted for N

Type Inference using Type Constraints Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution T 1: =[[N → N]*N→N] Tf: =[N→N] Tsqrt : = [N → N] Tnum 4: =N Tx: =N T 2: =N T 0: =N Equation 10: - step 1: T 2 is substituted: T 0=N - Step 3: Eq 10 is applied to the sub: Any occurrence of T 0 is substituted for N The inference succeeds! The type of T 0 is Number Exp: ((lambda ([f 1: [N->N]] [x 1: N]): N (f 1 x 1)) sqrt 4)

Type Inference using Type Constraints Question 2: Extending the typing mechanism for if expressions. Recall the typing rule for if expressions (if p c a): For every: type environment _Tenv, expressions _e 1, _e 2, _e 3, and type expressions _S 1, _S 2: if _Tenv |- _e 1: Boolean, _Tenv |- _e 2: _S 2, _Tenv |- _e 3: _S 2, Then _Tenv |- (if _e 1 _e 2 _e 3): _S 2 Observations: • P is of type Boolean • c and a have the same type: _S 2. • This is also the type for the entire if expression. What would be the equation for if in the constraints approach? For the expression (if p c a), construct: Tc=Ta, Tif =Tc

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) Exp: Typing the expression (if [#t: T#t] [(+ 1 2): T 1] [3: Tnum 3]): T 0 STAGE-I: Rename bound variables Not needed, no references of variables. STAGE-II: Assign type variables to all sub-exps Expression (if #t (+ 1 2) 3) (+ 1 2) + #t 1 2 3 Var T 0 T 1 T+ T#t Tnum 1 Tnum 2 Tnum 3

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-III: Construct type equations. 1. For atomic exps / primitive-procs, construct equations using their types. 2. For (lambda (v 1. . . vn) e 1. . . em), construct: T(lambda(v 1…vn) e 1…en) =[Tv 1*…*Tvn -> Ten] 3. For (f e 1. . . en), construct: Tf =[Te 1*…*Ten -> T(f e 1 … en)] 4. For (if p c a), construct: Tc=Ta, Tif =Tc Expression Equation (if #t (+ 1 2) 3) T 1=Tnum 3 T 0 = T 1 T+=[Tnum 1*Tnum 2 ->T 1] T+->[N*N->N] T#t = Boolean Tnum 1 = Number Tnum 2 = Number Tnum 3 = Number (+ 1 2) + #t 1 2 3 Expression (if #t (+ 1 2) 3) (+ 1 2) + #t 1 2 3 Var T 0 T 1 T+ T#t Tnum 1 Tnum 2 Tnum 3

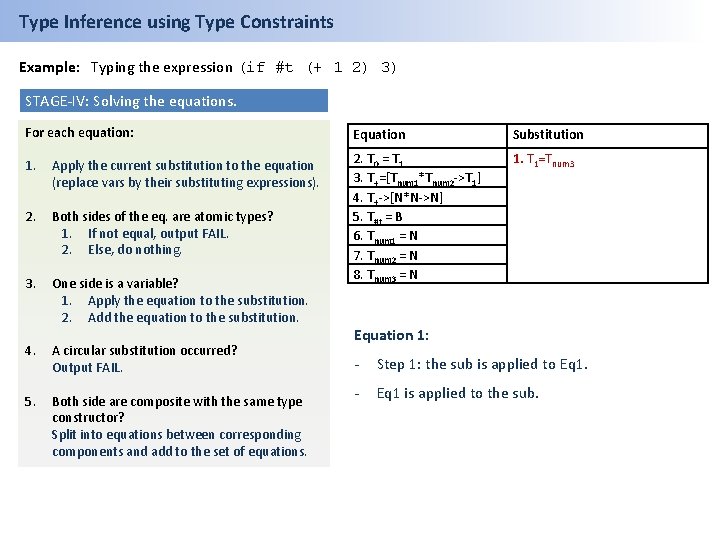
Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 1. T 1=Tnum 3 2. T 0 = T 1 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Substitution Equation 1: - Step 1: the sub is applied to Eq 1. - Eq 1 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 2. T 0 = T 1 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 1: - Step 1: the sub is applied to Eq 1. - Eq 1 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 2. T 0 = T 1 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - Step 1: T 1 is substituted: T 0 = Tnum 3 - Step 3: Eq 2 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 2. T 0 = Tnum 3 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - Step 1: T 1 is substituted: T 0 = Tnum 3 - Step 3: Eq 2 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. T 0 = Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - Step 1: T 1 is substituted: T 0 = Tnum 3 - Step 3: Eq 2 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. T 0 = Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. T+=[Tnum 1*Tnum 2 ->T 1] 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 3: - Step 1: The sub is applied to Eq 3: T+ = [Tnum 1*Tnum 2 ->Tnum 3] - Step 3: Eq 3 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. T+=[Tnum 1*Tnum 2 ->Tnum 3] 1. T 1=Tnum 3 2. T 0 = Tnum 3 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Substitution Equation 1: - Step 3: The sub is applied to Eq 3: T+ = [Tnum 1*Tnum 2 ->Tnum 3] - Step 3: Eq 3 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. 2. T 0 = Tnum 3 3. T+=[Tnum 1*Tnum 2 ->Tnum 3] Equation 1: - Step 3: The sub is applied to Eq 3: T+ = [Tnum 1*Tnum 2 ->Tnum 3] - Step 3: Eq 3 is applied to the sub.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. 2. T 0 = Tnum 3 3. T+=[Tnum 1*Tnum 2 ->Tnum 3] Equation 4: - Step 1: The sub is applied to Eq 4: [Tnum 1*Tnum 2 ->Tnum 3] = [N * N -> N] - Step 5: Eq 4 is split into existing equations, then removed.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 4. T+->[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. 2. T 0 = Tnum 3 3. T+=[Tnum 1*Tnum 2 ->Tnum 3] Equation 4: - Step 1: The sub is applied to Eq 4: [Tnum 1*Tnum 2 ->Tnum 3] = [N * N -> N] - Step 5: Eq 4 is split into existing equations, then removed.

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 1. T 1=Tnum 3 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. 2. T 0 = Tnum 3 3. T+=[Tnum 1*Tnum 2 ->Tnum 3] - Applying the sub to Eq 5 -8 makes no difference. - Applying the equations to the sub, we get…

Type Inference using Type Constraints Example: Typing the expression (if #t (+ 1 2) 3) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 1. T 1=N 2. T 0 = N 3. T+=[N*N->N] 5. T#t = B 6. Tnum 1 = N 7. Tnum 2 = N 8. Tnum 3 = N • The inference succeeds • The expression is well-typed • The type of T 0 is Number (if [#t: Boolean] [(+ 1 2): N] [3: N]): N

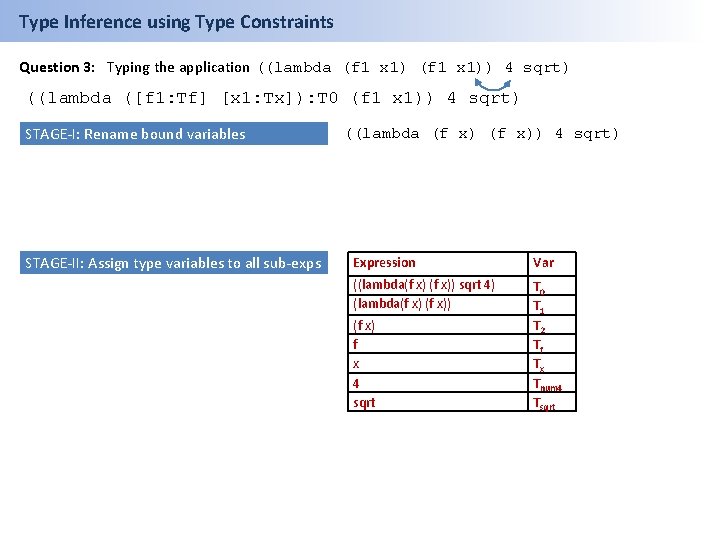
Type Inference using Type Constraints Question 3: Typing the application ((lambda (f 1 x 1)) 4 sqrt) ((lambda ([f 1: Tf] [x 1: Tx]): T 0 (f 1 x 1)) 4 sqrt) STAGE-I: Rename bound variables STAGE-II: Assign type variables to all sub-exps ((lambda (f x)) 4 sqrt) Expression Var ((lambda(f x)) sqrt 4) (lambda(f x)) T 0 T 1 T 2 Tf Tx Tnum 4 Tsqrt (f x) f x 4 sqrt

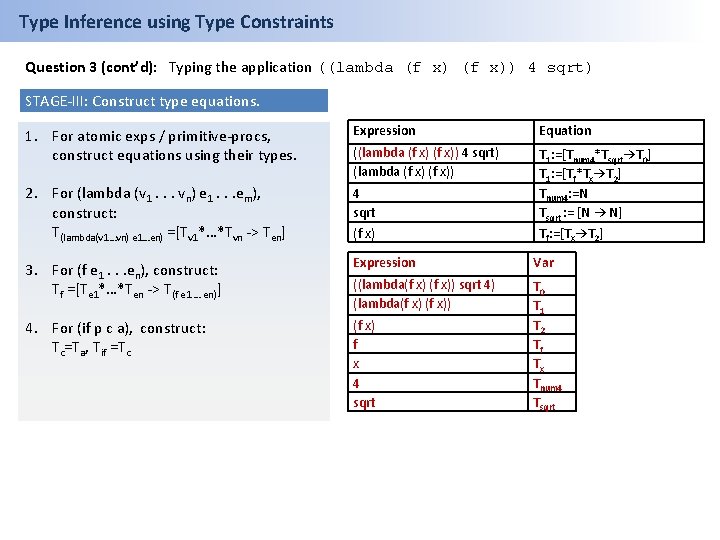
Type Inference using Type Constraints Question 3 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Construct type equations. 1. For atomic exps / primitive-procs, construct equations using their types. Expression Equation ((lambda (f x)) 4 sqrt) (lambda (f x)) 2. For (lambda (v 1. . . vn) e 1. . . em), construct: T(lambda(v 1…vn) e 1…en) =[Tv 1*…*Tvn -> Ten] 4 sqrt (f x) T 1: =[Tnum 4*Tsqrt→T 0] T 1: =[Tf*Tx→T 2] Tnum 4: =N Tsqrt : = [N → N] Tf: =[Tx→T 2] 3. For (f e 1. . . en), construct: Tf =[Te 1*…*Ten -> T(f e 1 … en)] Expression Var ((lambda(f x)) sqrt 4) (lambda(f x)) 4. For (if p c a), construct: Tc=Ta, Tif =Tc (f x) f x 4 sqrt T 0 T 1 T 2 Tf Tx Tnum 4 Tsqrt

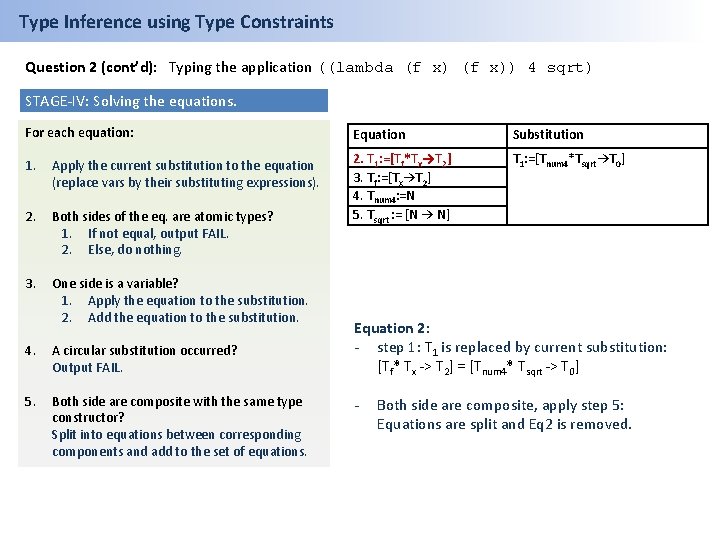
Type Inference using Type Constraints Question 3 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tnum 4*Tsqrt→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 2. T 1: =[Tf*Tx→T 2] 3. Tf: =[Tx→T 2] 4. Tnum 4: =N 5. Tsqrt : = [N → N] 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 1: - Apply step 1: Initially, the substitution is empty. - Eq 1 is moved to the substitution.

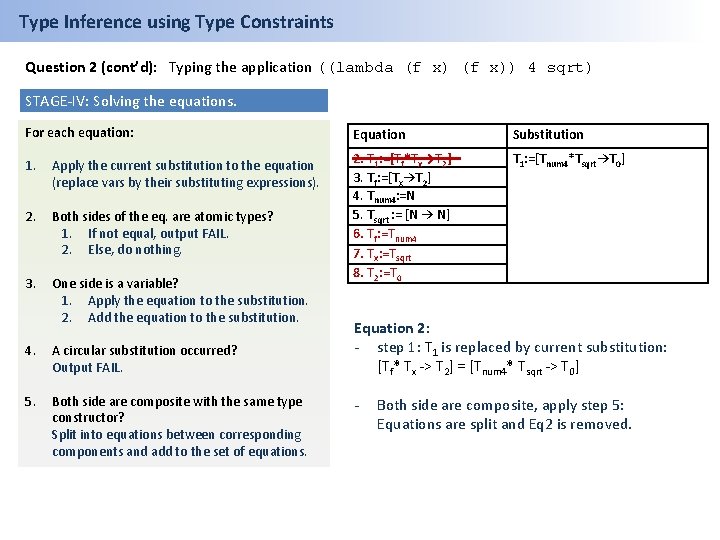
Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tnum 4*Tsqrt→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 2. T 1: =[Tf*Tx→T 2] 3. Tf: =[Tx→T 2] 4. Tnum 4: =N 5. Tsqrt : = [N → N] 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - step 1: T 1 is replaced by current substitution: [Tf* Tx -> T 2] = [Tnum 4* Tsqrt -> T 0] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tnum 4*Tsqrt→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 2. T 1: =[Tf*Tx→T 2] 3. Tf: =[Tx→T 2] 4. Tnum 4: =N 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 2: - step 1: T 1 is replaced by current substitution: [Tf* Tx -> T 2] = [Tnum 4* Tsqrt -> T 0] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: Equation Substitution 1. Apply the current substitution to the equation (replace vars by their substituting expressions). T 1: =[Tnum 4*Tsqrt→T 0] 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. Tf: =[Tx→T 2] 4. Tnum 4: =N 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation 3: - step 1: No change. - Eq 3 is added to the substitution.

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 4. Tnum 4: =N 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[Tnum 4*Tsqrt→T 0] Tf: =[Tx→T 2] Equation 3: - step 1: No change. - Eq 3 is added to the substitution.

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 4. Tnum 4: =N 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[Tnum 4*Tsqrt→T 0] Tf: =[Tx→T 2] Equation 4: - step 1: No change. - Eq 4 is added to the substitution: Any occurrence of Tnum 4 is substituted by N

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[N*Tsqrt→T 0] Tf: =[Tx→T 2] Tnum 4: =N Equation 4: - step 1: No change. - Eq 4 is added to the substitution: Any occurrence of Tnum 4 is substituted by N

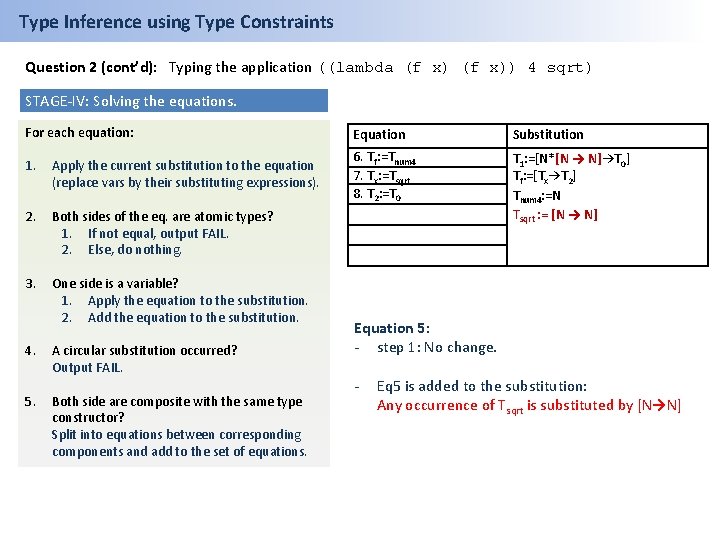
Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 5. Tsqrt : = [N → N] 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[N*Tsqrt→T 0] Tf: =[Tx→T 2] Tnum 4: =N Equation 5: - step 1: No change. - Eq 5 is added to the substitution: Any occurrence of Tsqrt is substituted by [N→N]

Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. 5. A circular substitution occurred? Output FAIL. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[N*[N → N]→T 0] Tf: =[Tx→T 2] Tnum 4: =N Tsqrt : = [N → N] Equation 5: - step 1: No change. - Eq 5 is added to the substitution: Any occurrence of Tsqrt is substituted by [N→N]

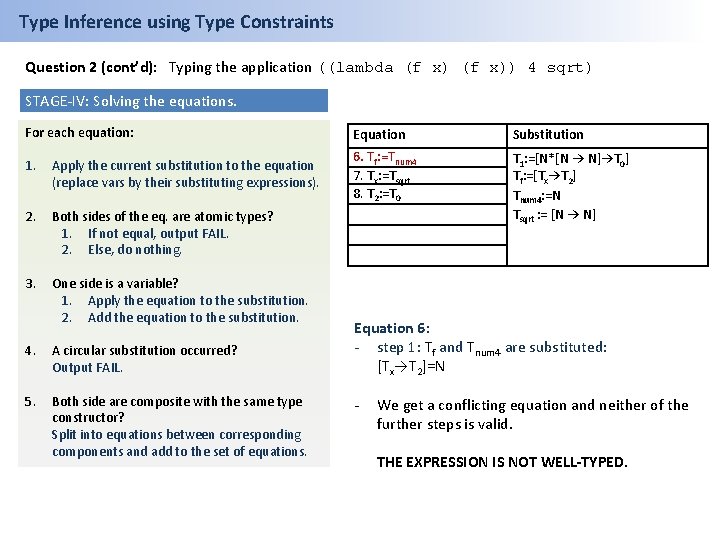
Type Inference using Type Constraints Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-IV: Solving the equations. For each equation: 1. Apply the current substitution to the equation (replace vars by their substituting expressions). 2. Both sides of the eq. are atomic types? 1. If not equal, output FAIL. 2. Else, do nothing. 3. One side is a variable? 1. Apply the equation to the substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components and add to the set of equations. Equation Substitution 6. Tf: =Tnum 4 7. Tx: =Tsqrt 8. T 2: =T 0 T 1: =[N*[N → N]→T 0] Tf: =[Tx→T 2] Tnum 4: =N Tsqrt : = [N → N] Equation 6: - step 1: Tf and Tnum 4 are substituted: [Tx→T 2]=N - We get a conflicting equation and neither of the further steps is valid. THE EXPRESSION IS NOT WELL-TYPED.