Type Checking Textbook Types and Programming Languages Benjamin

Type Checking Textbook: Types and Programming Languages Benjamin Pierce

Plan • • • Motivation (Chapter 1) Untyped Arithmetic Expressions (Chapter 3) Typed Arithmetic Expressions (Chapter 8) Untyped Lambda Calculus (Chapter 5) Typed Lambda Calculus (Chapter 9) Extensions

Challenges of Program Verification • Specification of software behavior • Reasoning about logical formulas • The annotation burden • The dynamic nature of software • Automatically infer safe invariants from the code • Concentrate on very simple properties with lightweight annotations

June 4, 1996 The European Ariane 5 rocket explodes 40 s into its maiden flight due to a software bug.

1997 Mars Rover Loses Contact 1999 Mars Climate Orbiter is Lost 1999 Mars polar Lander is lost 2004 Mar rover freezes

August 2005 As a Malaysia Airlines jetliner cruised from Perth, Australia, to Kuala Lumpur, Malaysia, one evening last August, it suddenly took on a mind of its own and zoomed 3, 000 feet upward. The captain disconnected the autopilot and pointed the Boeing 777's nose down to avoid stalling, but was jerked into a steep dive. He throttled back sharply on both engines, trying to slow the plane. Instead, the jet raced into another climb. The crew eventually regained control and manually flew their 177 passengers safely back to Australia. Investigators quickly discovered the reason for the plane's roller-coaster ride 38, 000 feet above the Indian Ocean. A defective software program had provided incorrect data about the aircraft's speed and acceleration, confusing flight computers. August 2005

Type Systems • A tractable syntactic method for proving absence of certain program behaviors by classifying phrases according to the kinds they compute • Examples – – Whenever f is called, its argument must be integer The arguments of f are not aliased The types of dimensions must match …

What is a type • A denotation of set of values – Int – Bool –… • A set of legal operations

Static Type Checking • Performed at compile-time • Conservative (sound but incomplete) – if <complex test> then 5 else <type error> • Usually limited to simple properties – – Prevents runtime errors Enforce modularity Protects user-defined abstractions Allows tractable analysis • Properties beyond scope (usually) – Array out of bound – Division by zero – Non null reference

Error detection • Early error detection – Logical errors – Interface errors – Dimension analysis – Effectiveness also depends on the programmer – Can be used for code maintenance

Abstraction • Types define interface between different software components • Enforces disciplined programming • Ease software integration

Documentation • Types are useful for reading programs • Can be used by language tools

Language Safety • A safe programming language protects its own abstraction • Can be achieved by type safety

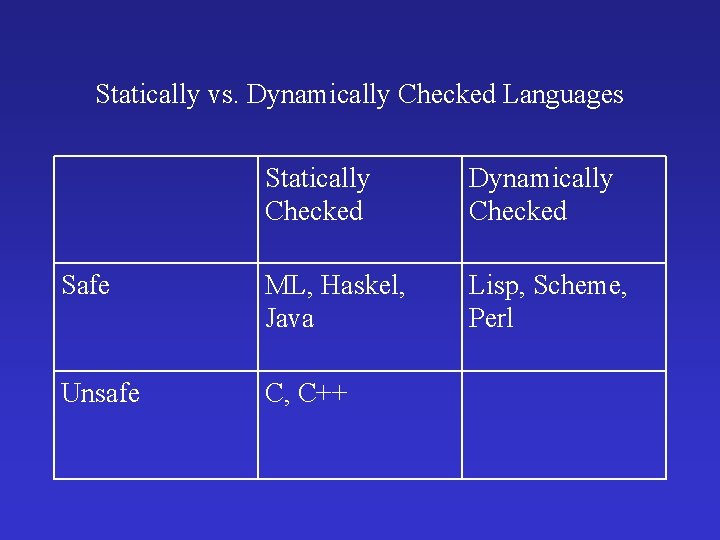
Statically vs. Dynamically Checked Languages Statically Checked Dynamically Checked Safe ML, Haskel, Java Lisp, Scheme, Perl Unsafe C, C++

Eiffel, 1989 Cook, W. R. (1989) - A Proposal for Making Eiffel Type-Safe, in Proceedings of ECOOP'89. S. Cook (ed. ), pp. 57 -70. Cambridge University Press. Betrand Meyer, on unsoundness of Eiffel: “Eiffel users universally report that they almost never run into such problems in real software development. ”

Ten years later: Java

Efficiency • Compilers can used types to optimize computations • Pointer scope (Titanium) • Region inference

Language Design • Design the programming language with the type system • But types incur some notational overhead • Implicit vs. explicit types – The annotation overhead

Untyped Arithmetic Expressions Chapter 3

Untyped Arithmetic Expressions t : : = terms true constant true false constant false if t then t else t conditional 0 constant zero succ t successor pred t predecessor izzero test if false then 0 else 1 1 iszero (pred (succ 0)) true

Untyped Arithmetic Expressions t : : = terms true constant true false constant false if t then t else t conditional 0 constant zero succ t successor pred t predecessor izzero test succ true type error if 0 then 0 else 0 type error

SOS for Booleans t : : = terms t 1 t’ 1 true constant true false constant false if false then t else t t (E-IFFALSE) 1 2 2 conditional t 1 t’ 1 (E-IF) values if t 1 then t 1 else t 2 if t then t else t v : : = true false if true then t 1 else t 2 t 1 (E-IFTRUE) if t’ 1 then t 1 else t 2

SOS for Numbers t : : = terms 0 constant zero succ t successor pred t predecessor iszero test v : : = values true value false nv false value numeric values nv : : = numeric values 0 zero value succ nv successor value t 1 t’ 1 t 1 t’ 1 succ t 1 succ t’ 1 (E-SUCC) pred 0 0 (E-PREDZERO) pred (succ nv 1) nv 1 (E-PREDSUCC) t 1 t’ 1 pred t’ 1 iszero 0 true (E-PRED) (E-ISZERO) iszero (succ nv 1) false (E-ISZEROSUCC) t 1 t’ 1 iszero t 1 iszero t’ 1 (E-ISZERO)

Typed Arithmetic Expressions Chapter 8

Stuck Computations • The goal of the type system is to ensure at compile-time that no stuck ever occurs at runtime • Safety (soundness) – Progress: A well-typed term t never gets stuck • Either it has value or there exists t’ such that t t’ – Preservation (subject reduction) • If well type term takes a step in evaluation, then the resulting term is also well typed

Type Rules for Boolean T : : = Bool types type of Boolean t: T true : Bool (T-TRUE) false : Bool (T-FALSE) t 1 : Bool t 2 : T t 3 : T (T-IF) if t 1 then t 2 else t 3 : T

Type Rules for Numbers T : : = Nat types type of Natural numbers t: T 0 : Nat (T-ZERO) t 1 : Nat succ(t 1) : Nat t 1 : Nat pred(t 1) : Nat t 1 : Nat iszero(t 1) : Bool T-SUCC T-PRED ISZERO

The Typing Relation • Formally the typing relation is the smallest binary relation between terms and types – in terms of inclusion • A term t is typable (well typed) if there exists some type T such that t : T

Inversion of the typing relation • • true : R R = Bool false : R R = Bool if t 1 then t 2 else t 3 : R t 1: Bool, t 2 : R, t 3: R 0 : R R = Nat succ t 1 : R R = Nat and t 1 : Nat pred t 1 : R R = Nat and t 1 : Nat iszero t 1 : R R = Bool and t 1 : Nat

Uniqueness of Types • Each term t has at most one type – If t is typable then • its type is unique • There is a unique type derivation tree for t

Safety • Canonical Forms: – If v is a value of type Boolean then v =true or v=false – If v is a value of type Nat then v belongs to nv nv : : = numeric values 0 zero value succ nv successor value • Progress : If t is well defined then either t is a value or for some t’: t t’ • Preservation: if t : T and t t’ then t’ : T

Untyped Lambda Calculus Chapter 5

Untyped Lambda Calculus t : : = terms x variable x. t abstraction tt application ( x. x) Syntactic Conventions • Applications associates to left • The body of abstraction extends as far as possible

Scope • An occurrence of x is free in a term t if it is not in the body on an abstraction x. t – otherwise it is bound – x is a binder • FV: t P(Var) is the set free variables of t – FV(x) = {x} – FV( x. t) = FV(t) – {x} – FV (t 1 t 2) = FV(t 1) FV(t 2) • Terms w/o free variables are combinators – Example: x. x

Operational Semantics ( x. t 12) t 2 [x t 2] t 12 ( -reduction) [x s]x =s if y x [x s]y=y [x s ] ( y. t 1) = y. [x s ] t 1 if y x and y FV(s) [x s ] (t 1 t 2) = ([x s ] t 1) ([x s ] t 2) ( x. x) y y ( x. x) ) (u r) u r ( x. x) ( x ( y. x y)) (y z) ( x ( w. x w)) (y z) w. y z w

Operational Semantics ( x. t 12) t 2 [x t 2] t 12 ( -reduction) [x s]x =s if y x [x s]y=y [x s ] ( y. t 1) = y. [x s ] t 1 if y x and y FV(s) [x s ] (t 1 t 2) = ([x s ] t 1) ([x s ] t 2) Evaluation orders: • Full beta reduction • Normal order • Call by name • Call by value ( x. x)( z. ( x. x) z((

Programming in the Lambda Calculus • Turing complete • Multiple arguments – (x, y). s = x. y. s • Church Booleans – tru = t. f. t – fls = t. f. f – test = l. m. n. l m n – and = b. c. b c fls • Pairs – pair = f. b. s. b f s – fst = p. p tru – snd = p. p fls • Church Numerals – c 0 = f. z. z – c 1 = f. z. s z – c 2 = f. z. s (s z) – c 3 = f. z. s (s (s z)) • Divergence – omega= ( x. x x)

Summary Lambda Calculus • • Powerful Useful to illustrate ideas But can be counterintuitive Usually extended with useful syntactic sugars

Simple Typed Lambda Calculus Chapter 9

Simple Typed Lambda Calculus t : : = terms x variable x: T. t abstraction tt application T: : = T T types of functions

SOS for Simple Typed Lambda Calculus t : : = terms x variable x: T. t abstraction tt application v: : = x: T. t T: : = T T t 1 t 2 t 1 t’ 1 t 2 t’ 2 values abstraction values t 1 t 2 t 1 t’ 2 (E-APP 1) (E-APP 2) ( x: T 11. t 12) t 2 [x t 2] t 12 (E-APPABS) types of functions

Type Rules t : : = terms x variable x: T. t abstraction t : T x : T (T-VAR) , x : T 1 t 2 : (T-ABS) T x : T 1. 2 t 2 : T 1 T 2 T: : = T T : : = t 1 : T 11 t 2 : T 11 (T-APP) T 12 t 1 t 2 : T 12 types of functions types context empty context , x : T term variable binding

t : T t : : = terms x variable x: T. t abstraction tt application true constant true false constant false if t then t else t conditional x : T (T-VAR) , x : T 1 t 2 : (T-ABS) T x : T 1. 2 t 2 : T 1 T 2 t 1 : T 11 t 2 : T 11 (T-APP) T 12 t 1 t 2 : T 12 true : Bool (T-TRUE) T: : = types Bool T T : : = Boolean types of functions context empty context , x : T term variable binding false : Bool (T-FALSE) t 1 : Bool t 2 : T t 3 : T if t 1 then t 2 else t 3 : T (T-IF)

Examples • ( x: Bool. x ) true • if true then ( x: Bool. x) else ( x: Bool. x) • if true then ( x: Bool. x) else ( x: Bool. y: Bool. x)

The Typing Relation • Formally the typing relation is the smallest ternary relation on contexts, terms and types – in terms of inclusion • A term t is typable in a given context (well typed) if there exists some type T such that t : T

Inversion of the typing relation • x : R x: R • x : T 1. t 2 : R R = T 1 R 2 for some R 2 with t 2 : R 2 • t 1 t 2 : R there exists T 11 such that t 1 : T 11 R and t 2 : T 11 • true : R R = Bool • false : R R = Bool • if t 1 then t 2 else t 3 : R t 1: Bool, t 2 : R, t 3: R

Uniqueness of Types • Each term t has at most one type in any given context – If t is typable then • its type is unique • There is a unique type derivation tree for t

Safety • Canonical Forms: – If v is a value of type Boolean then v =true or v=false – If v is a value of type T 1 T 2 then v = x. T 1. t 2 • Progress : If t is closed and well defined ( t : T for some T) then either t is a value of for some t’: t t’ • Permutation: if t : T and is a permutation of then t: T • Weakening: if t : T and x dom( ) then , x : S t : T • Preservation of types under substitution: – If , x : S t : T and s : S then [x s] t : T • Preservation: if t : T and t t’ then t’ : T

Implicit vs. Explicit Types • Do we have to spell out the type of every argument? • Implicit type systems allow the programmers to omit the types as long as the resulting type is unique – Reduces the annotation burden • A type inference algorithm infers a unique type or issues an error

Other Issues • The Curry-Howard Correspondence • Erasure of typability • Curry-Stlyle vs. Church style of languages definition

Extensions • Subtyping (Chapters 15 -19) – Most general type • Recursive Types (Chapters 20, 21) – Nat. List = <Nil: Unit, cons: {Nat, Nat. List}> • Polymorphism (Chapters 22 -28) – length: list int – Append: list • Higher-order systems (Chapters 29 -32)

Summary • Type systems provide a useful for enforcing certain safety properties – Can be combined with runtime systems and program analysis • Interacts with the programmer • A lot of interesting theory