Type Checking and Type Inference cs 3180 Prasad

Type Checking and Type Inference cs 3180 (Prasad) Poly. Types 1

Motivation • Application Programmers – Reliability • Logical and typographical errors manifest themselves as type errors that can be caught mechanically, thereby increasing our confidence in the code execution. • Language Implementers – Storage Allocation (temporaries) – Generating coercion code – Optimizations cs 3180 (Prasad) Poly. Types 2

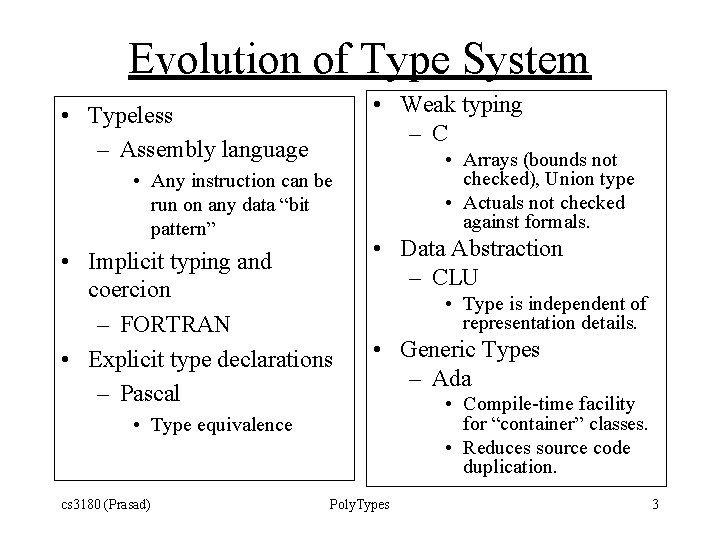
Evolution of Type System • Weak typing – C • Typeless – Assembly language • Any instruction can be run on any data “bit pattern” • Implicit typing and coercion – FORTRAN • Explicit type declarations – Pascal • Arrays (bounds not checked), Union type • Actuals not checked against formals. • Data Abstraction – CLU • Type is independent of representation details. • Generic Types – Ada • Type equivalence cs 3180 (Prasad) Poly. Types • Compile-time facility for “container” classes. • Reduces source code duplication. 3

• Languages – Strongly typed (“Type errors always caught. ”) • Statically typed (e. g. , ML, Ada, Eiffel, and Scala) – Compile-time type checking : Efficient. • Dynamically typed (e. g. , Scheme, Python, and Smalltalk) – Run-time type checking : Flexible. – Weakly typed (e. g. , C) – Unreliable Casts (int to/from pointer). – Typing in Object-Oriented Languages • OOPLs, such as Eiffel and Java, impose restrictions that guarantee type safety and efficiency, but bind the code to function names at run-time. cs 3180 (Prasad) Poly. Types 4

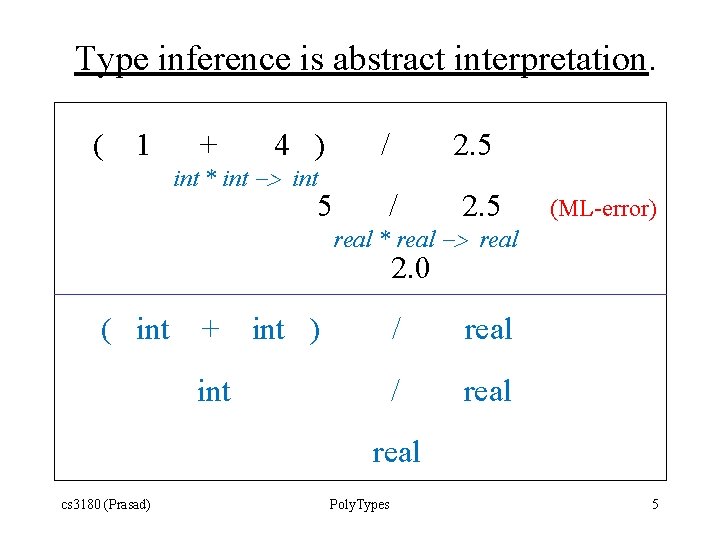
Type inference is abstract interpretation. ( 1 + 4 ) / 2. 5 5 / 2. 5 int * int -> int real * real -> real (ML-error) 2. 0 ( int + int ) int / real cs 3180 (Prasad) Poly. Types 5

Expression Grammar: Type Inference Example E -> E + E | E * E | x | y | i | j • Arithmetic Evaluation x, y in {…, -1. 1, …, 2. 3, …} i, j in {…, -1, 0, 1, …} +, * : “infinite table” • Type Inference x, y i, j cs 3180 (Prasad) : real : int Poly. Types 6

Values can be abstracted as type names and arithmetic operations can be abstracted as operations on these type names. cs 3180 (Prasad) Poly. Types 7

Type correctness is neither necessary nor sufficient for programs to run. if true then 5 else 0. 5 • Not type correct, but runs fine. if true then 1. 0/0. 0 else 3. 5 • Type correct, but causes run-time error. cs 3180 (Prasad) Poly. Types 8

Assigning types to expressions (ML) • Uniquely determined fn s => s ^ “. n”; val it = fn : string -> string • Over-constrained (type error in ML) (2. 5 + 2) • Under-constrained – Overloading fn x => fn y => x + y; (* resolvable *) fn record => #name(record); (* error *) – Polymorphism fn x => 1 ; val it = fn : 'a -> int cs 3180 (Prasad) Poly. Types 9

Type Signatures : Curried functions • fun rdivc x y = x / y rdivc : real -> real • fun rdivu (x, y) = x / y rdivu : real * real -> real • fun plusi x y = x + y plusi : int -> int • fun plusr (x: real, y) = x + y plusr : real * real -> real cs 3180 (Prasad) Poly. Types 10

Polymorphic Types • Semantics of operations on data structures such as stacks, queues, lists, and tables are independent of the component type. • Polymorphic type system provides a natural representation of generic data structures without sacrificing type safety. • Polymorphism fun I x = x; I 5; I “x”; 4 for all types a: I: a -> a cs 3180 (Prasad) Poly. Types 11

Programming with Lists in ML Polymorphic Types, Type Inference and Pattern Matching cs 3180 (Prasad) Poly. Types 12

Lists a is a type -----a list is a type (* Homogeneous lists. *) – E. g. , (true, [fn i: int => "i"]) : bool * (int -> string) list; – E. g. , [1, 2, 3], 1: : 2: : 3: : [] : int list; – E. g. , (op : : ) : ’a * ’a list ->’a list; – List constructors [] and : : can be used in patterns. cs 3180 (Prasad) Poly. Types 13

Built-in operations on lists hd : ’a list -> ’a tl : ’a list -> ’a list null: ’a list -> bool op @ : ’a list * ’a list -> ’a list (* append operation; infix operator *) length : ’a list -> int (* sets vs lists -- multiplicity; ordering *) cs 3180 (Prasad) Poly. Types 14

Catalog of List functions init [1, 2, 3] last [1, 2, 3] = [1, 2] = 3 • Specs: init (xs last (xs @ [x]) = x • Definitions: fun | cs 3180 (Prasad) init last (x: : []) (x: : xs) Poly. Types = = [] x : : init xs; x last xs; 15

take drop 3 [1, 2, 3, 4] 2 [1, 2, 3] = [3] • Definition: fun | | take 0 xs = [] n [] = [] n (x: : xs) = x: : take (n-1) xs; fun | | drop 0 xs = xs n [] = [] n (x: : xs) = drop (n-1) xs; cs 3180 (Prasad) Poly. Types 16

• Role of patterns – For testing type (“discrimination”) – For picking sub-expressions apart • Inferred Signatures (Captures correct usage) init: ’a list -> ’a list last: ’a list -> ’a take, drop : int -> ’a list List. take, List. drop : ’a list * int -> ’a list cs 3180 (Prasad) Poly. Types 17

takewhile even [2, 4, 1, 6, 2] = [2, 4] Definition: fun | takewhile p [] = [] takewhile p (x: : xs) = if p x then x : : takewhile p xs else []; takewhile: (’a -> bool) -> ’a list cs 3180 (Prasad) Poly. Types 18

dropwhile even [2, 3, 8] = [3, 8] • Definition: fun dropwhile p [] = [] | dropwhile p (x: : xs) = if p x then dropwhile p xs else x: : xs; dropwhile : (’a -> bool) -> ’a list cs 3180 (Prasad) Poly. Types 19

Composition val h = f o g; fun comp f g = let fun h x = f (g x) in h; comp: (a -> b) -> (l->a) -> (l->b) – Generality + Correct Usage – Equality constraints cs 3180 (Prasad) Poly. Types 20

map-function fun map f [] = [] | map f (x: : xs) = f x : : map f xs map : (a -> b) -> (a list) map (fn x => “n”) map (fn x => x: : []) -> (b list) [1, 2, 3] [“a”, “b”] • list patterns; term matching. • definition by cases; ordering of rules cs 3180 (Prasad) Poly. Types 21

Conventions • Function application is left-associative. f g h = ( ( f g ) h ) • -> is right-associative. int->real->bool = int->(real->bool) • : : is right-associative. a: : b: : c: : [] = a: : (b: : (c: : []) • Function application binds stronger than : : . f x : : xs = ( f x ) : : xs (a -> b) -> (b -> c) =/= (a -> b -> c) cs 3180 (Prasad) Poly. Types 22