Tycho Brahe 1546 1601 danski astronom i znanstvenik

Tycho Brahe (1546. - 1601. ), danski astronom i znanstvenik. Za života je bio poznat i kao astrolog i alkemičar. Jedan od najvećih astronoma-praktičara u povijesti.

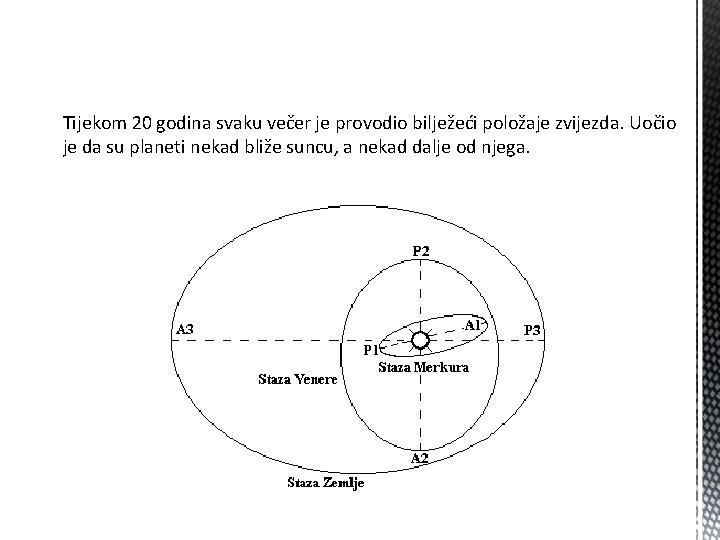
Tijekom 20 godina svaku večer je provodio bilježeći položaje zvijezda. Uočio je da su planeti nekad bliže suncu, a nekad dalje od njega.

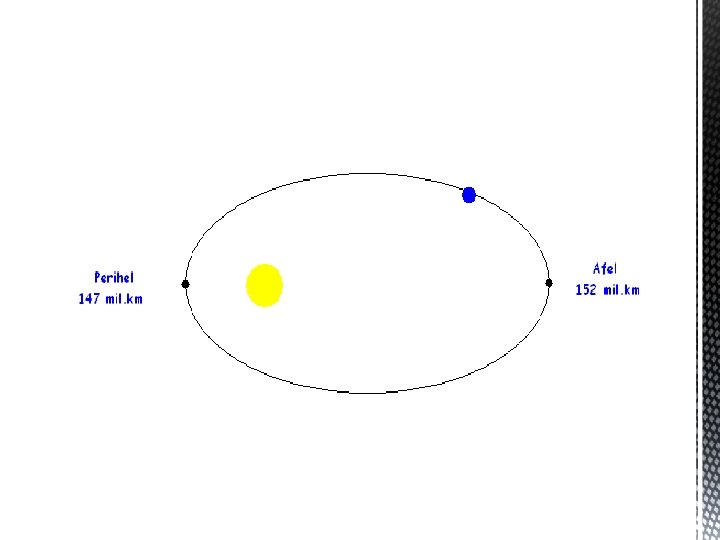
Uz pomoć njegovog rada Johannes Kepler (1571. - 1630. ), njemački astronom, pokazao je da se planeti gibaju po elipsama, a ne kružnicama.

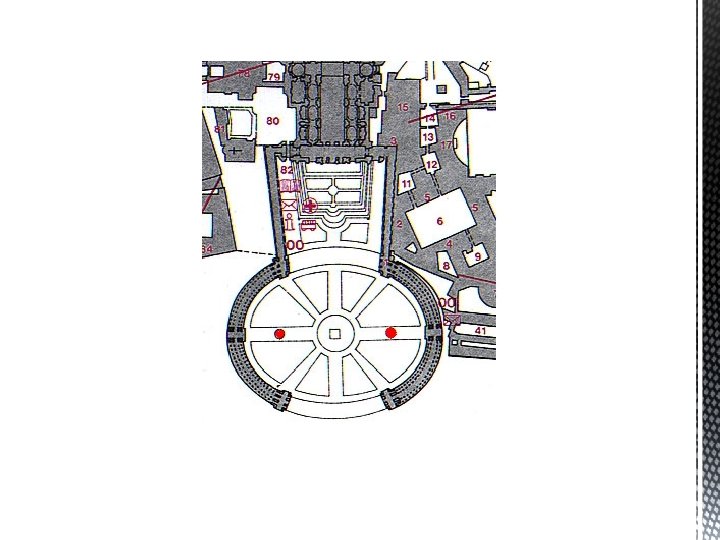
§ U arhitekturi baroka najčešće se koristi elipsa § Većina svodova izgrađenih u baroku ima oblik elipse

§ nastao je kao rezultat želje da se uobliči prostor ispred veličanstvene Bazilike koja dominira prostorom. § projektirao ga je veliki Bernini, a dovršen je u svega deset godina (1657. – 1667. ) prema odluci pape Aleksandra VII.

Elipsa je skup neprekinuto povezanih točaka ravnine za koje je zbroj udaljenosti od dvije čvrste točke te ravnine konstantan.

Čvrste točke F 1 i F 2 nazivamo žarištima ili fokusima elipse, a udaljenosti točke T elipse od žarišta radij-vektorima r 1 i r 2 te točke. Vrijedi: r 1 + r 2 = 2 a r 1= d(T, F 1) r 2 = d(T, F 2)

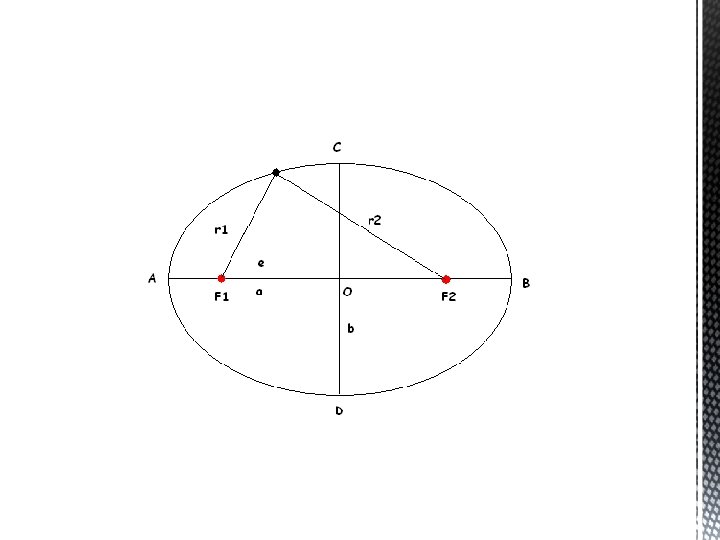
§ Točku O koja je polovište dužine F 1 F 2 zovemo središte ili centar elipse. § Točke A, B, C i D zovemo tjemena ili vrhovi elipse. § Dužina AB naziva se velika os, a dužine OA i OB velike poluosi elipse. § Dužina CD naziva se mala os, a dužine OC i OD male poluosi. § Polovica udaljenosti između žarišta je broj e koji nazivamo linearni ekscentricitet.

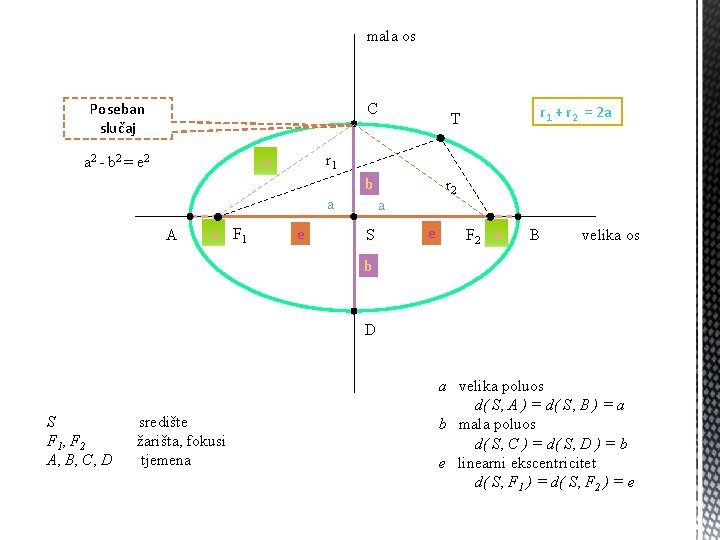
mala os Poseban slučaj C r 1 a a 2 - b 2 = e 2 b a A a F 1 r 1 + r 2 = 2 a T e r 2 a S e F 2 a B velika os b D S F 1, F 2 A, B, C, D središte žarišta, fokusi tjemena a velika poluos d( S, A ) = d( S, B ) = a b mala poluos d( S, C ) = d( S, D ) = b e linearni ekscentricitet d( S, F 1 ) = d( S, F 2 ) = e

§ Iz definicije imamo |F 1 D| + |F 2 D| = 2 a, a kako vidimo na slici |F 1 D| = |F 2 D| =a § Iz Pitagorina teorema tada slijedi e²+b²=a² odnosno, nakon sređivanja dobijemo: a²-b²=e²

Jednadžba elipse sa središtem u ishodištu i osima koje leže na koordinatnim osima glasi: b²x² + a²y² = a²b²

§ http: //www. authorstream. com/Presentation/a. SGuest 17109 -177731 konstrukcija-elipse-enter-tags-elipsa-education-ppt-powerpoint/

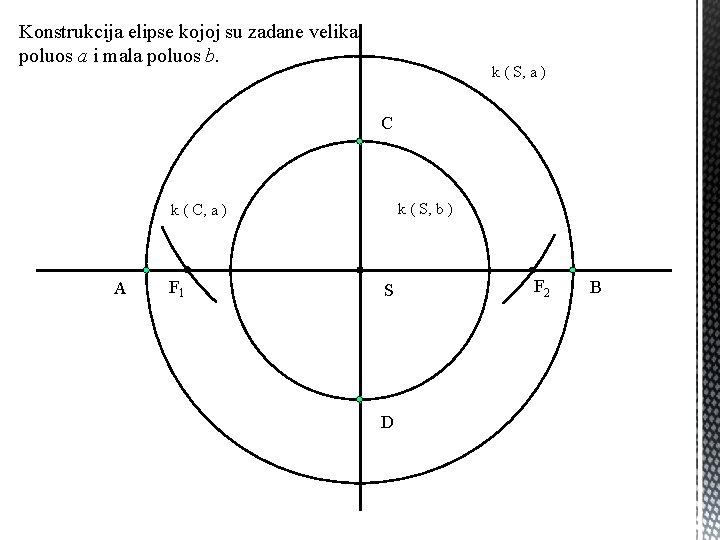
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. k ( S, a ) C k ( S, b ) k ( C, a ) A F 1 S D F 2 B

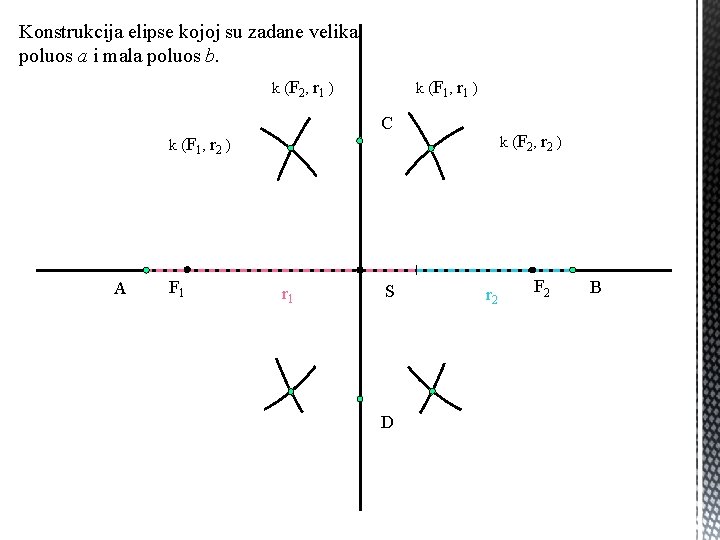
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. k (F 2 , r 1 ) k (F 1 , r 1 ) C k (F 2 , r 2 ) k (F 1 , r 2 ) A F 1 r 1 S D r 2 F 2 B

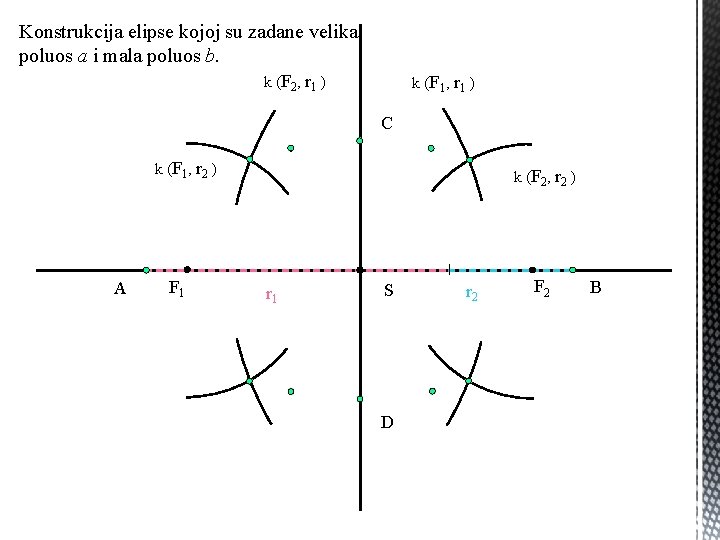
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. k (F 2 , r 1 ) k (F 1 , r 1 ) C k (F 1 , r 2 ) A F 1 k (F 2 , r 2 ) r 1 S D r 2 F 2 B

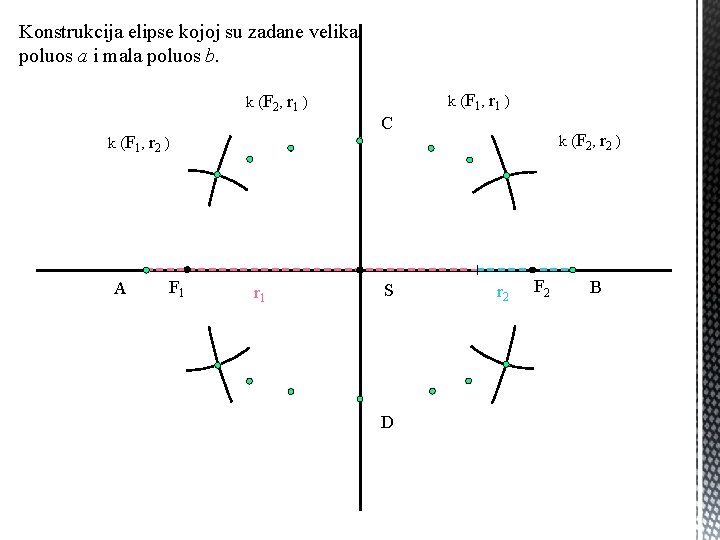
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. k (F 2 , r 1 ) k (F 1 , r 2 ) A F 1 r 1 k (F 1 , r 1 ) C S D k (F 2 , r 2 ) r 2 F 2 B

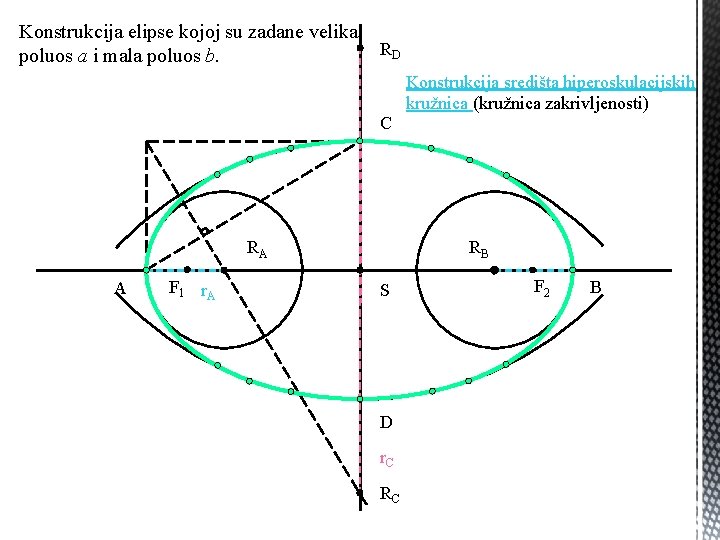
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. RD C RB RA A F 1 r. A Konstrukcija središta hiperoskulacijskih kružnica (kružnica zakrivljenosti) S D r. C RC F 2 B

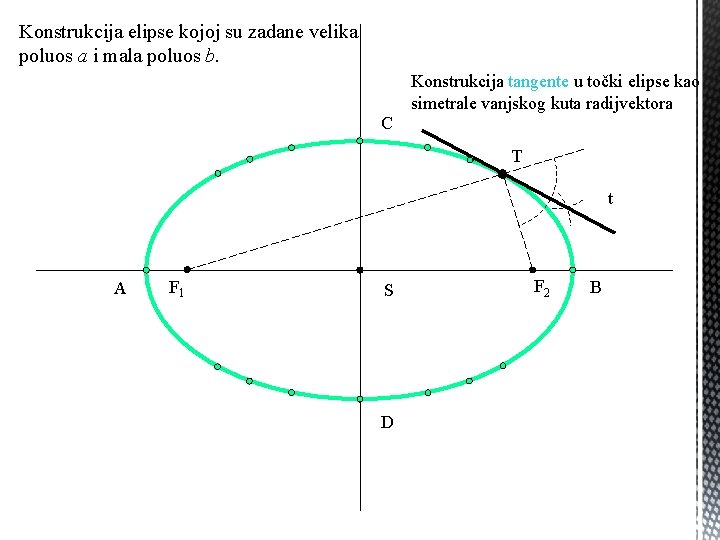
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. Konstrukcija tangente u točki elipse kao simetrale vanjskog kuta radijvektora C T t A F 1 S D F 2 B

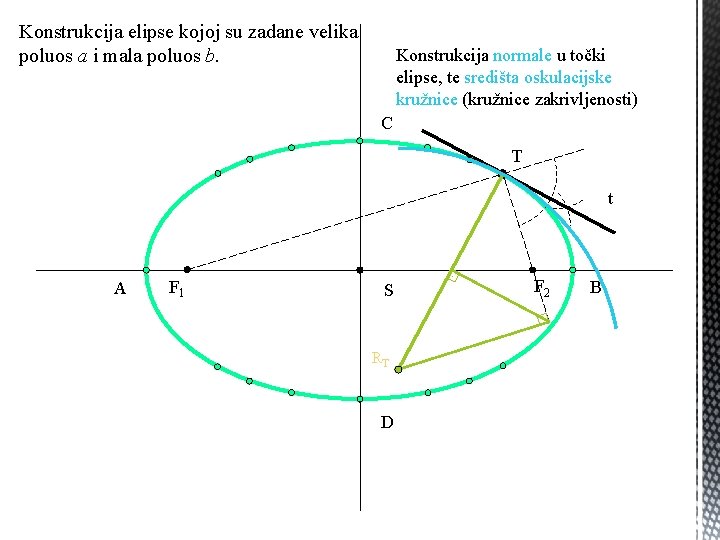
Konstrukcija elipse kojoj su zadane velika poluos a i mala poluos b. Konstrukcija normale u točki elipse, te središta oskulacijske kružnice (kružnice zakrivljenosti) C T t A F 1 . S RT D F 2 B

Odredi duljinu male i velike osi te udaljenost žarišta elipse ako je dana njezina jednadžba: 9 x 2+25 y 2=225

Velika os elipse iznosi 8 cm, a linearni ekscentricitet 3 cm. Kako glasi jednadžba te elipse?

Nacrtajmo elipsu 25 x² + 9 y² = 225

Dobijemo kružnicu.

Vrhovi trokuta su žarišta elipse x² + 4 y² = 12 i središte kružnice x 2+y 2 -2 x-6 y+9=0. Kolika je površina trokuta?