TwoSource Constructive and Destructive Interference Conditions Crests Troughs

Two-Source Constructive and Destructive Interference Conditions

Crests Troughs

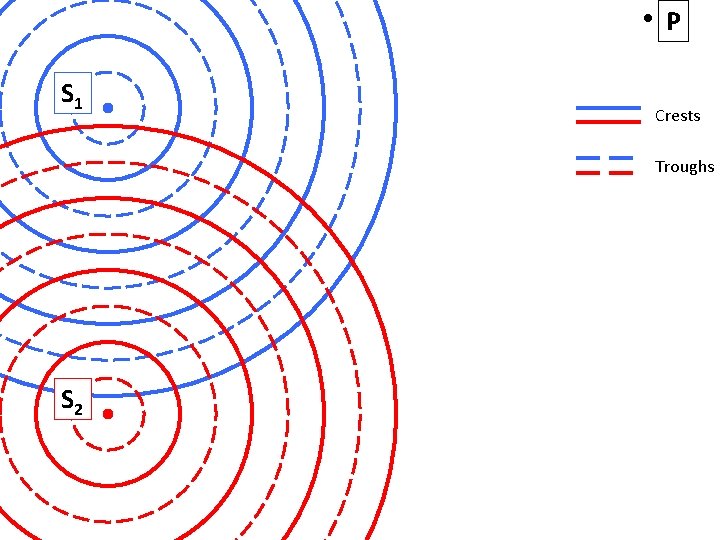
P S 1 Crests Troughs S 2

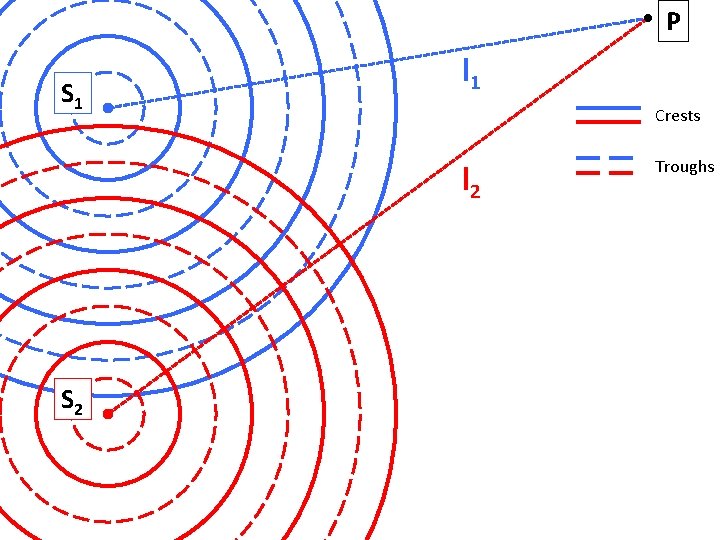
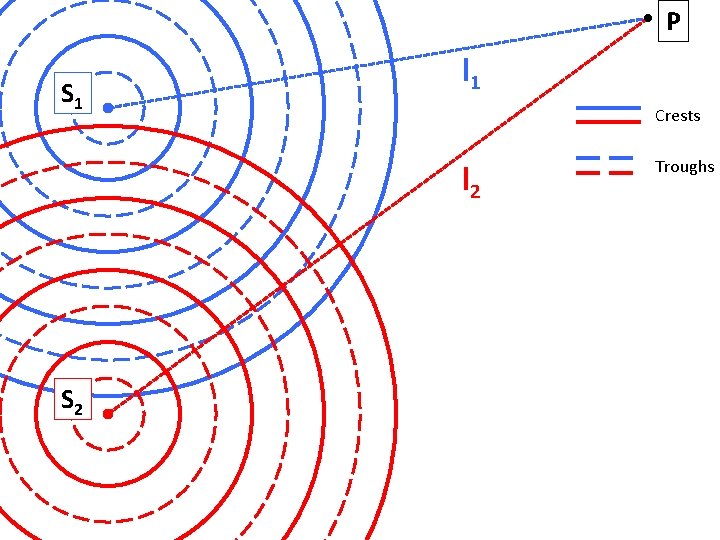
P S 1 l 1 Crests l 2 S 2 Troughs

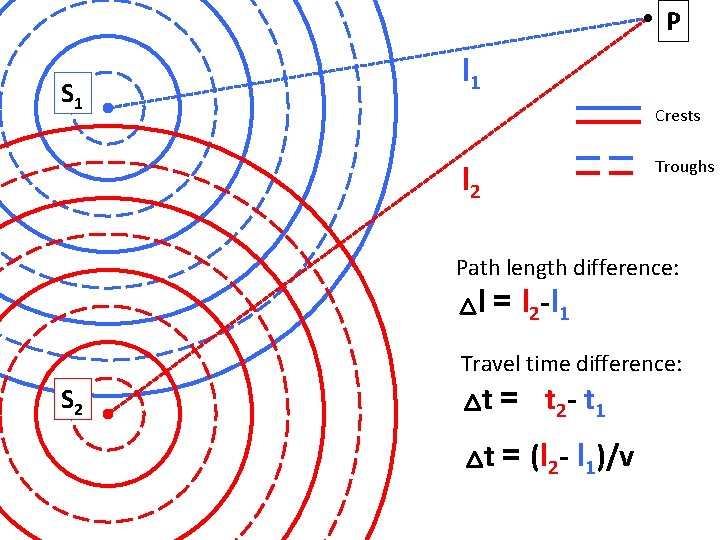
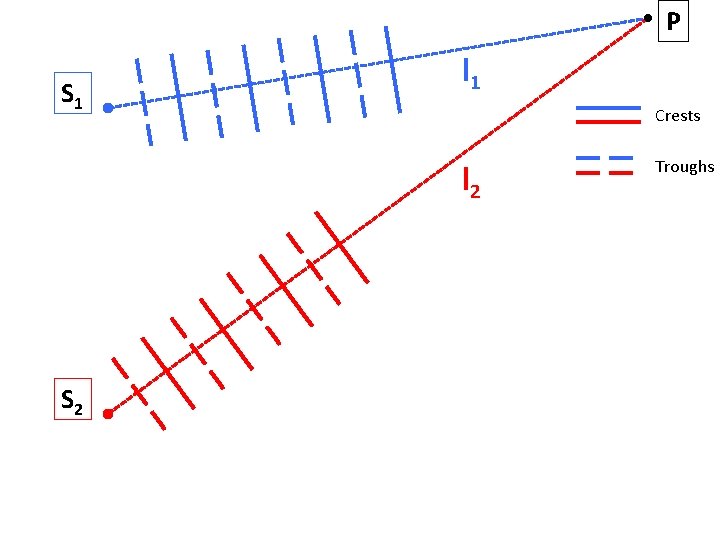
P S 1 l 1 Crests Troughs l 2 Path length difference: l = l 2 -l 1 Travel time difference: S 2 t = t 2 - t 1 t = (l 2 - l 1)/v

P S 1 l 1 Crests l 2 S 2 Troughs

P S 1 l 1 Crests l 2 S 2 Troughs

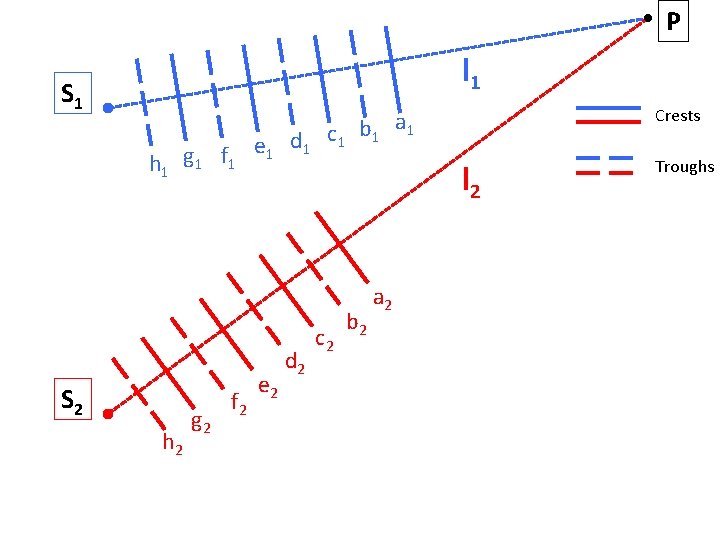
P l 1 S 1 h 1 g 1 f 1 S 2 h 2 g 2 f 2 e 1 d 1 e 2 d 2 Crests a c 1 b 1 1 l 2 c 2 b 2 a 2 Troughs

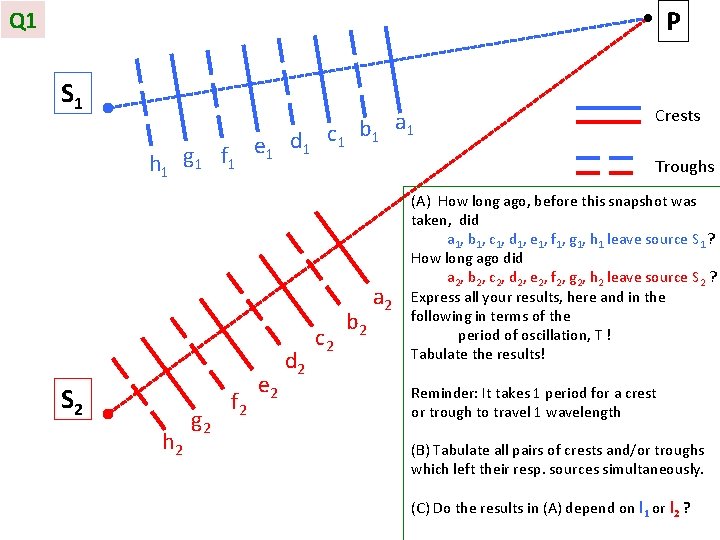
P Q 1 S 1 h 1 g 1 f 1 S 2 h 2 g 2 f 2 e 1 d 1 e 2 d 2 a c 1 b 1 1 Crests Troughs c 2 b 2 a 2 (A) How long ago, before this snapshot was taken, did a 1, b 1, c 1, d 1, e 1, f 1, g 1, h 1 leave source S 1 ? How long ago did a 2, b 2, c 2, d 2, e 2, f 2, g 2, h 2 leave source S 2 ? Express all your results, here and in the following in terms of the period of oscillation, T ! Tabulate the results! Reminder: It takes 1 period for a crest or trough to travel 1 wavelength (B) Tabulate all pairs of crests and/or troughs which left their resp. sources simultaneously. (C) Do the results in (A) depend on l 1 or l 2 ?

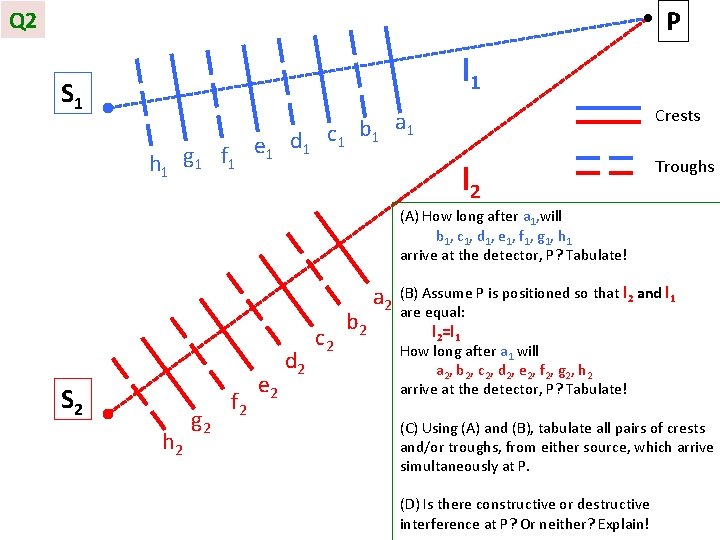
P Q 2 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 and l 1 are equal: l 2=l 1 How long after a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

P Q 3 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 exceeds l 1 by one wavelength, λ: l 2=l 1 + λ How long after a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

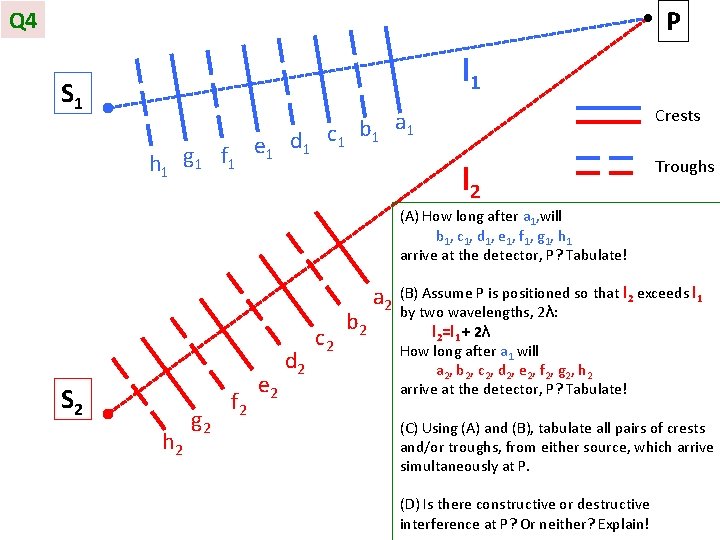
P Q 4 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 exceeds l 1 by two wavelengths, 2λ: l 2=l 1 + 2λ How long after a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

P Q 5 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 is shorter than l 1 by two wavelengths, 2λ: l 2=l 1 - 2λ How long after (+) or before (-) a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

P Q 6 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 exceeds l 1 by one half-wavelengths, λ/2: l 2=l 1 + λ/2 How long after (+) or before (-) a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

P Q 7 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 is shorter than l 1 by three half-wavelengths, 3λ/2: l 2=l 1 - 3λ/2 How long after (+) or before (-) a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

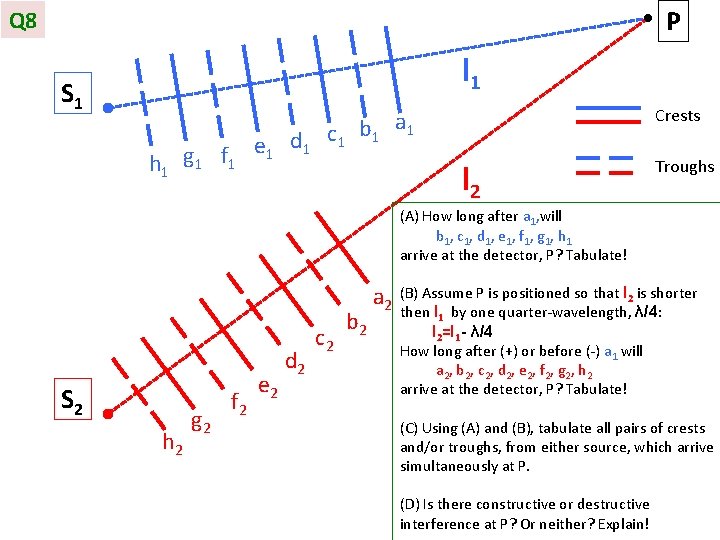
P Q 8 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 is shorter then l 1 by one quarter-wavelength, λ/4: l 2=l 1 - λ/4 How long after (+) or before (-) a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

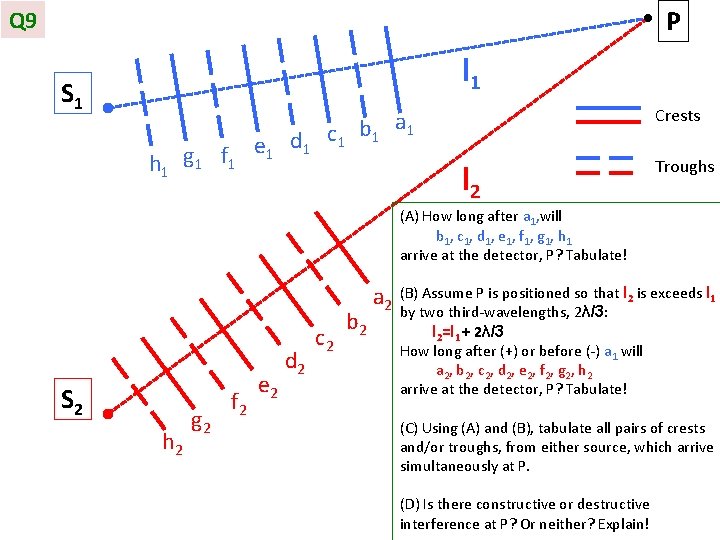
P Q 9 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 l 2 Troughs (A) How long after a 1, will b 1 , c 1 , d 1 , e 1 , f 1 , g 1 , h 1 arrive at the detector, P? Tabulate! S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 (B) Assume P is positioned so that l 2 is exceeds l 1 by two third-wavelengths, 2λ/3: l 2=l 1 + 2λ/3 How long after (+) or before (-) a 1 will a 2 , b 2 , c 2 , d 2 , e 2 , f 2 , g 2 , h 2 arrive at the detector, P? Tabulate! (C) Using (A) and (B), tabulate all pairs of crests and/or troughs, from either source, which arrive simultaneously at P. (D) Is there constructive or destructive interference at P? Or neither? Explain!

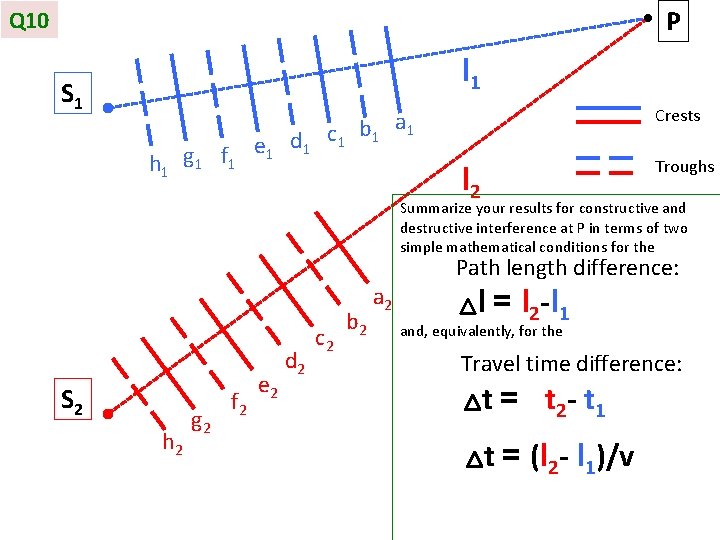
P Q 10 l 1 S 1 h 1 g 1 f 1 e 1 d 1 Crests a c 1 b 1 1 Troughs l 2 Summarize your results for constructive and destructive interference at P in terms of two simple mathematical conditions for the S 2 h 2 g 2 f 2 e 2 d 2 c 2 b 2 a 2 Path length difference: l = l 2 -l 1 and, equivalently, for the Travel time difference: t = t 2 - t 1 t = (l 2 - l 1)/v

Constructive Interference =Intensity Maximum: Destructive Interference =Intensity Minimum: Path length difference: l = l 2 -l 1= m λ Travel time difference: t = t 2 - t 1 = m T m= 0, +1, -1, +2, -2, … l = l 2 -l 1= (m+1/2) λ Travel time difference: t = t 2 - t 1 = (m+1/2) T (m+1/2) = +1/2, -1/2, +3/2, -3/2, … where the period T is: T= λ/v

Interference Pathlength Geometry

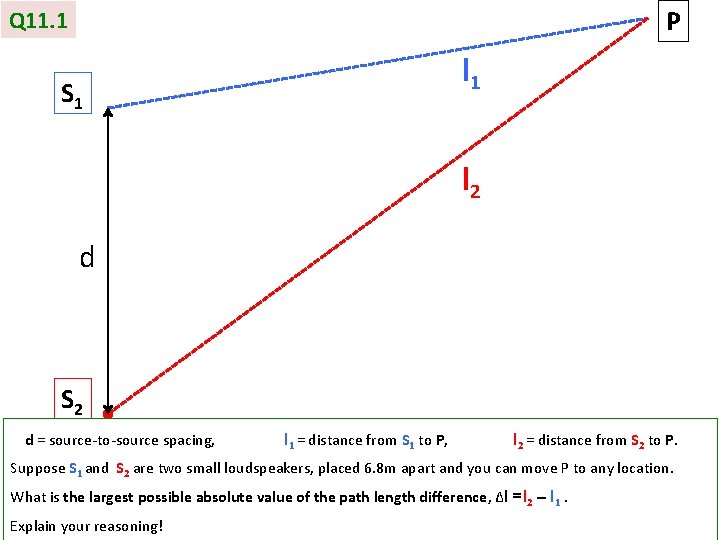
P Q 11. 1 l 1 S 1 l 2 d S 2 d = source-to-source spacing, l 1 = distance from S 1 to P, l 2 = distance from S 2 to P. Suppose S 1 and S 2 are two small loudspeakers, placed 6. 8 m apart and you can move P to any location. What is the largest possible absolute value of the path length difference, Δl =l 2 – l 1. Explain your reasoning!

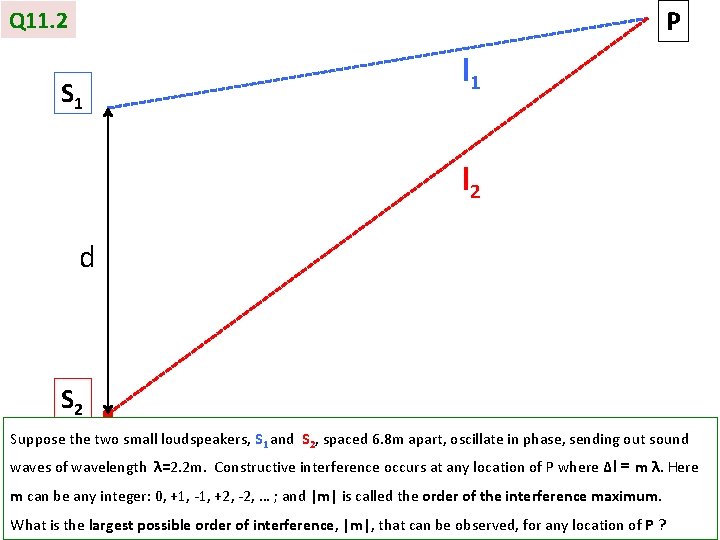
P Q 11. 2 S 1 l 2 d S 2 Suppose the two small loudspeakers, S 1 and S 2, spaced 6. 8 m apart, oscillate in phase, sending out sound waves of wavelength λ=2. 2 m. Constructive interference occurs at any location of P where Δl = m λ. Here m can be any integer: 0, +1, -1, +2, -2, … ; and |m| is called the order of the interference maximum. What is the largest possible order of interference, |m|, that can be observed, for any location of P ?

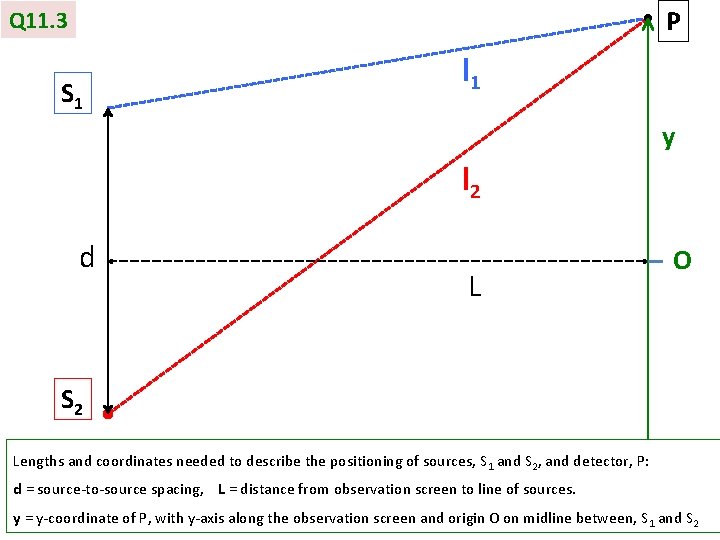
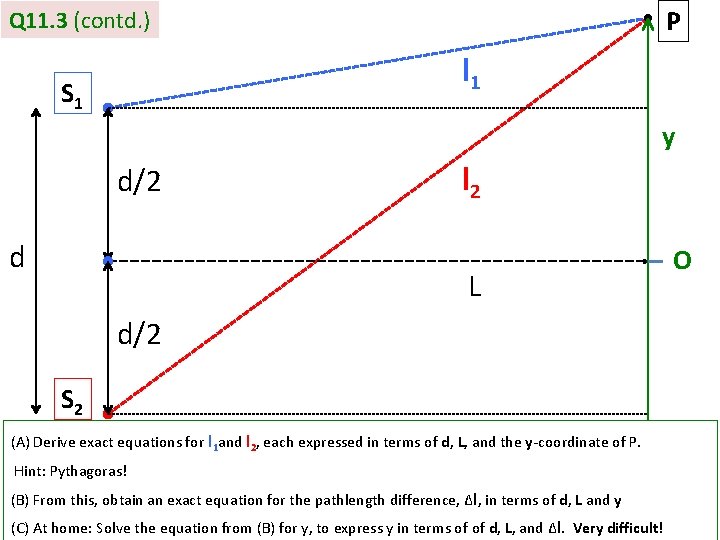
P Q 11. 3 S 1 l 1 y l 2 d L O S 2 Lengths and coordinates needed to describe the positioning of sources, S 1 and S 2, and detector, P: d = source-to-source spacing, L = distance from observation screen to line of sources. y = y-coordinate of P, with y-axis along the observation screen and origin O on midline between, S 1 and S 2

P Q 11. 3 (contd. ) l 1 S 1 y d/2 d l 2 L d/2 S 2 (A) Derive exact equations for l 1 and l 2, each expressed in terms of d, L, and the y-coordinate of P. Hint: Pythagoras! (B) From this, obtain an exact equation for the pathlength difference, Δl, in terms of d, L and y (C) At home: Solve the equation from (B) for y, to express y in terms of of d, L, and Δl. Very difficult! O

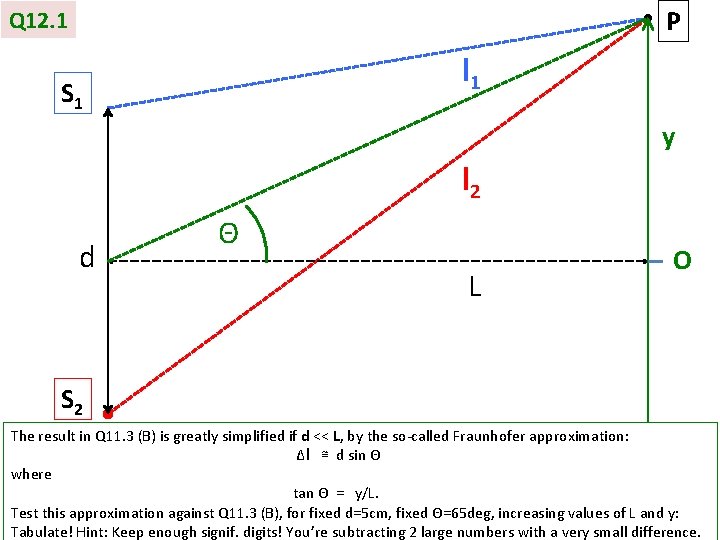
P Q 12. 1 l 1 S 1 y l 2 d Θ L O S 2 The result in Q 11. 3 (B) is greatly simplified if d << L, by the so-called Fraunhofer approximation: Δl ≅ d sin Θ where tan Θ = y/L. Test this approximation against Q 11. 3 (B), for fixed d=5 cm, fixed Θ=65 deg, increasing values of L and y: Tabulate! Hint: Keep enough signif. digits! You’re subtracting 2 large numbers with a very small difference.

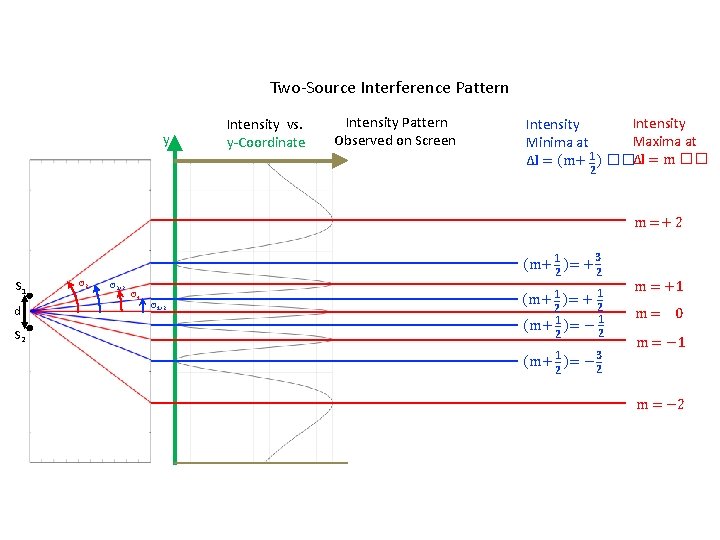
Two-Source Interference Pattern y Intensity vs. y-Coordinate Intensity Pattern Observed on Screen Intensity Maxima at Minima at 1 Δl = (m+ _ ) ��Δl = m �� 2 m =+ 2 S 1 d S 2 Θ 3/2 (m+ _1 )= + _32 2 Θ 1/2 1 (m+ _1 )= + _2 2 1 (m+ 1_ )= − _2 2 (m+ 1_ )= − _32 2 m = +1 m= 0 m = − 1 m = − 2

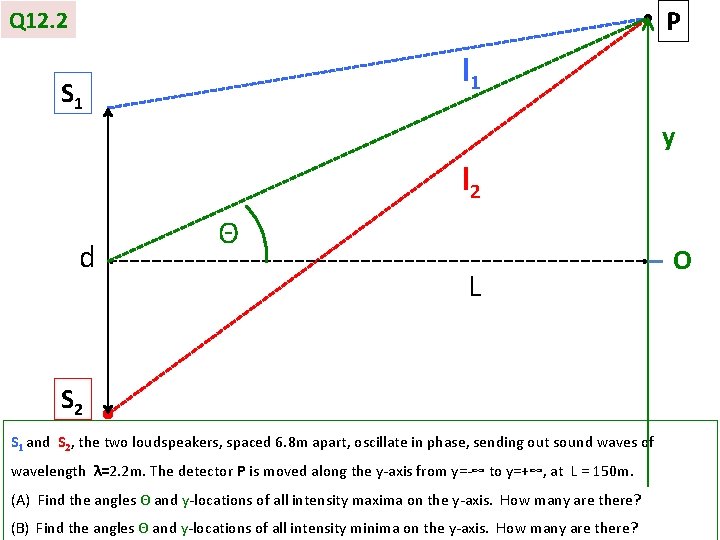
P Q 12. 2 l 1 S 1 y l 2 d Θ L S 2 S 1 and S 2, the two loudspeakers, spaced 6. 8 m apart, oscillate in phase, sending out sound waves of wavelength λ=2. 2 m. The detector P is moved along the y-axis from y=-∞ to y=+∞, at L = 150 m. (A) Find the angles Θ and y-locations of all intensity maxima on the y-axis. How many are there? (B) Find the angles Θ and y-locations of all intensity minima on the y-axis. How many are there? O

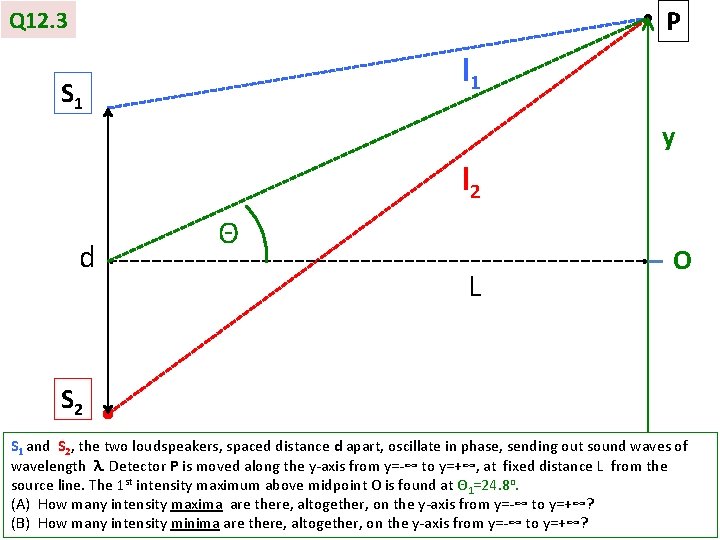
P Q 12. 3 l 1 S 1 y l 2 d Θ L O S 2 S 1 and S 2, the two loudspeakers, spaced distance d apart, oscillate in phase, sending out sound waves of wavelength λ. Detector P is moved along the y-axis from y=-∞ to y=+∞, at fixed distance L from the source line. The 1 st intensity maximum above midpoint O is found at Θ 1=24. 8 o. (A) How many intensity maxima are there, altogether, on the y-axis from y=-∞ to y=+∞? (B) How many intensity minima are there, altogether, on the y-axis from y=-∞ to y=+∞?

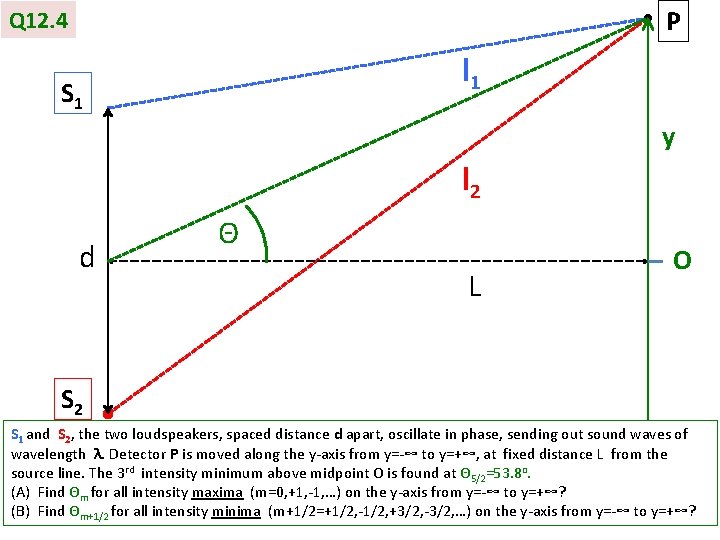
P Q 12. 4 l 1 S 1 y l 2 d Θ L O S 2 S 1 and S 2, the two loudspeakers, spaced distance d apart, oscillate in phase, sending out sound waves of wavelength λ. Detector P is moved along the y-axis from y=-∞ to y=+∞, at fixed distance L from the source line. The 3 rd intensity minimum above midpoint O is found at Θ 5/2=53. 8 o. (A) Find Θm for all intensity maxima (m=0, +1, -1, …) on the y-axis from y=-∞ to y=+∞? (B) Find Θm+1/2 for all intensity minima (m+1/2=+1/2, -1/2, +3/2, -3/2, …) on the y-axis from y=-∞ to y=+∞?

Multi-Slit Constructive Interference Pathlength Geometry Intensity Plots

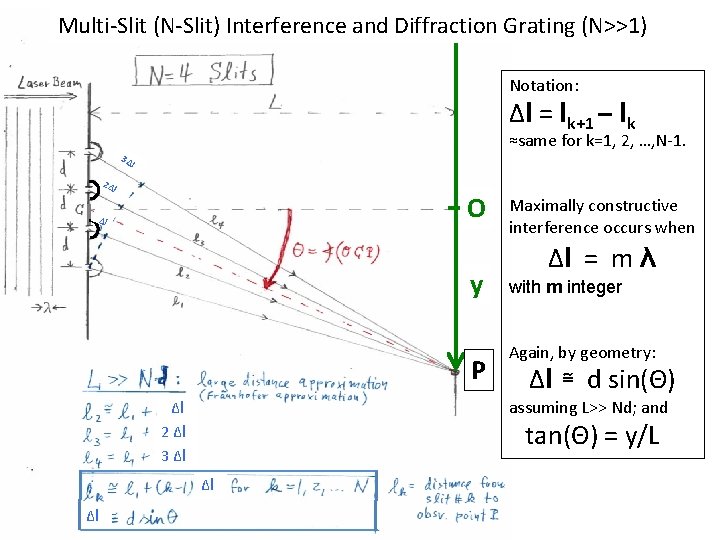
Multi-Slit (N-Slit) Interference and Diffraction Grating (N>>1) Notation: Δl = lk+1 – lk 3Δ 2Δ ≈same for k=1, 2, …, N-1. l l O Δl y P Δl = m λ with m integer Again, by geometry: Δl ≅ d sin(Θ) assuming L>> Nd; and Δl 2 Δl 3 Δl tan(Θ) = y/L Δl Δl Maximally constructive interference occurs when

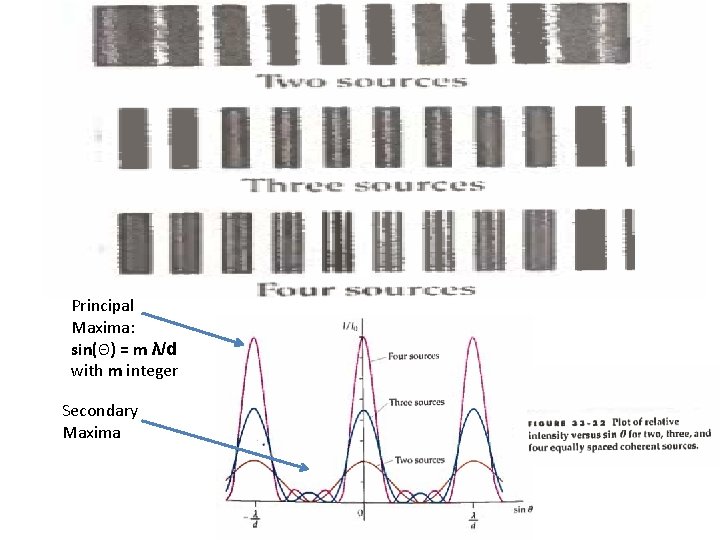
Principal Maxima: sin(Θ) = m λ/d with m integer Secondary Maxima

Q 13 A diffraction grating placed parallel to an observation screen, 40 cm from the screen, Is illuminated at normal incidence by coherent, monochromatic light (a laser beam). Assume Fraunhofer conditions (L>> Nd) are satisfied. (a) If the 1 st order principal maximum is observed on the screen 30 cm above the central maximum, how many principal maxima altogether, incl. central maximum, are observable? (b) If the 2 nd order principal maximum is observed on the screen 30 cm above the central maximum, how many principal maxima altogether, incl. central maximum, are observable? Find the angles, Θ, and y-coordinates of all principal maxima on the screen: Tabulate! (c) How would your answers change if the device had been a double-slit (N=2) or a quintuple-slit (N=5) instead of a diffraction grating?