TwoSample Inference Procedures with Means TwoSample Procedures When

Two-Sample Inference Procedures with Means

Two-Sample Procedures When we with means compare, • what are we The goal of these inferenceinterested The selection of the individual or objects in? procedures is to compare that make up one sample can not influence the selectionto of two individuals or objects inor the responses treatments other sample. to compare the characteristics of two populations • We have INDEPENDENT samples from each treatment or population

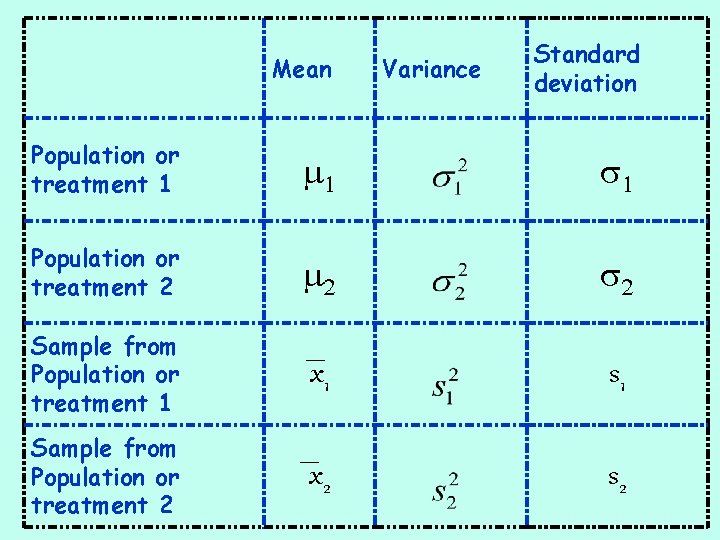
Notation When comparing two populations or treatments we must use notation that distinguishes between characteristics of the first and those of the second. (to do this we use subscripts)

Mean Variance Standard deviation Population or treatment 1 m 1 s 1 Population or treatment 2 m 2 s 2 Sample from Population or treatment 1 x 1 s 1 Sample from Population or treatment 2 x 2 s 2

Remember: We will be interested in the difference of means, so we will use this to find standard error.

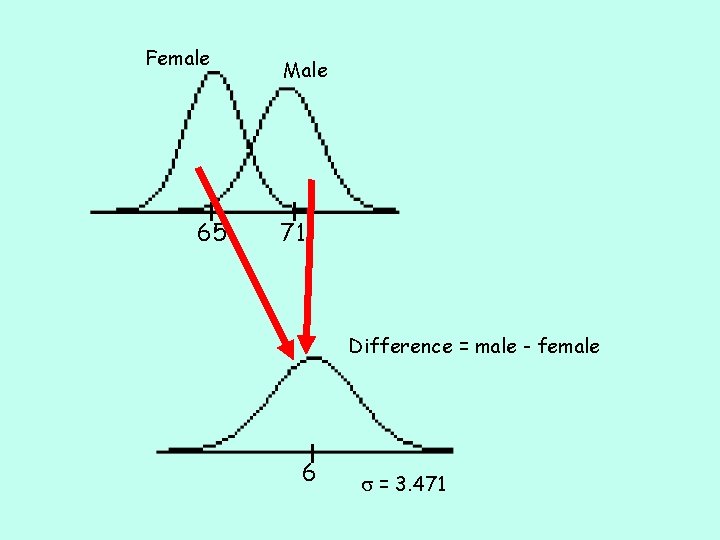
Suppose we have a population of adult men with a mean height of 71 inches and standard deviation of 2. 6 inches. We also have a population of adult women with a mean height of 65 inches and standard deviation of 2. 3 inches. Assume heights are normally distributed. Describe the distribution of the difference in heights between males and females (malefemale). Normal distribution with mx-y =6 inches & sx-y =3. 471 inches

Female 65 Male 71 Difference = male - female 6 s = 3. 471

a) What is the probability that the height of a randomly selected man is at most 5 inches taller than the height of a randomly selected woman? P((x. M-x. F) < 5) = normalcdf(-∞, 5, 6, 3. 471) =. 3866 b) What is the 70 th percentile for the difference (male-female) in heights of a randomly selected man & woman? (x. M-x. F) = inv. Norm(. 7, 6, 3. 471) = 7. 82

Do calculator simulation! To simulate the sampling distribution of the difference in means: • Select a random sample of 30 men and record their heights. – Randnorm(71, 2. 6, 30) L 1 – Find the sample mean for the mean height of men x m=

Do calculator simulation! Select a random sample of 30 women and record their heights. – Randnorm(65, 2. 3, 30) L 2 – Find the sample mean for the mean height of women x w= Find the difference in the sample means x m - x w=

Let’s Make a Dot Plot Looking at the sampling distribution of the difference in sample means: • What is the mean of the difference in sample means? • What is the standard deviation of the difference in sample means?

Examples: a) What is the probability that the mean height of 30 men is at most 5 inches taller than the mean height of 30 women? P((xm – xw)< 5) =. 0573 b) What is the 70 th percentile for the difference (male-female) in mean heights of 30 men and 30 women? 6. 332 inches

Constructing Confidence Intervals to Compare Two-Sample Means • Assumptions • Calculations • Conclusion

Assumptions: • Have two SRS’s from the populations or two randomly assigned treatment groups • Samples are independent • Both distributions are approximately normal – Have large sample sizes – Graph BOTH sets of data • s’s known/unknown

Formulas Since in real-life, we will NOT know both s’s, we will do t-procedures.

Degrees of Freedom Option 1: use the smaller of the two values n 1 – 1 and n 2 – 1 This will produce conservative results – higher p-values & lower confidence. Calculator Option 2: approximation used bydoes this automatically! technology

Confidence Called intervals: standard error

Pooled procedures: • Used for two populations with the same variance • When you pool, you average the two -sample variances to estimate the common population variance. • DO NOT use on AP Exam!!!!! We do NOT know the variances of the population, so ALWAYS tell the calculator NO for pooling!

Conclusion: We are __% confident that the true difference in mean CONTEXT is between _____ and _____.

Two competing headache remedies claim to give fastacting relief. An experiment was performed to compare the mean lengths of time required for bodily absorption of brand A and brand B. Assume the absorption time is normally distributed. Twelve people were randomly selected and given an oral dosage of brand A. Another 12 were randomly selected and given an equal dosage of brand B. The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: mean SD n Brand A 20. 1 8. 7 12 Brand B 18. 9 7. 5 12 Describe the shape & standard error for sampling distribution of the differences in the mean speed of absorption. (answer on next screen)

Describe the sampling distribution of the differences in the mean speed of absorption. Normal distribution with S. E. = 3. 316 Find a 95% confidence interval difference in mean lengths of time required for bodily absorption of each brand. (answer on next screen)

Assumptions: State assumptions! Have 2 independent randomly assigned treatments Given the absorption rate is normally distributed s’s unknown Formula & calculations From calculator df = Conclusion in context We are 95% confident that the true difference in mean 21. 53, use t* for df = lengths of time required for bodily absorption of each 21 & 95% confidence brand is between – 5. 685 minutes and 8. 085 minutes. level

Hypothesis Test with Two Samples

Hypothesis Statements: H 0 : m 1 = - m 2 = 0 Ha : H Haa: : m 1<- mm 22 < 0 m 1>- mm 22 > 0 mm 11 -≠ mm 22 ≠ 0 Be sure to define BOTH m 1 and m 2!

Hypothesis Test: Since we usually assume H 0 is true, then this equals 0 – so we can usually leave it out

The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: Brand A Brand B mean 20. 1 18. 9 SD 8. 7 7. 5 n 12 12 Is there sufficient evidence that these drugs differ in the speed at which they enter the blood stream?

Have 2 independent randomly assigned treatments State assumptions! Given the absorption rate is normally distributed s’s unknown H 0: m. A= m. B Ha: m. A= m. B Hypotheses & define variables! Where m. A is the true mean absorption time for Brand A & m. B is the true mean absorption time for Brand B Formula & calculations Conclusion in context Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that these drugs differ in the speed at which they enter the blood stream.

Suppose that the sample mean of Brand B is 16. 5, then is Brand B faster? No, I would still fail to reject the null hypothesis.

Robustness: • Two-sample procedures are more robust than one-sample procedures • BEST to have equal sample sizes! (but not necessary)

A modification has been made to the process for producing a certain type of time-zero film (film that begins to develop as soon as the picture is taken). Because the modification involves extra cost, it will be incorporated only if sample data indicate that the modification decreases true average development time by more than 1 second. Should the company incorporate the modification? Original 8. 6 5. 1 4. 5 5. 4 Modified 5. 5 4. 0 3. 8 6. 0 6. 3 6. 6 5. 8 4. 9 5. 7 8. 5 7. 0 5. 7

Assume we have 2 independent SRS of film Both distributions are approximately normal due to approximately symmetrical boxplots s’s unknown H 0: m. O- m. M = 1 Ha: m. O- m. M > 1 Where m. O is the true mean developing time for original film & m. M is the true mean developing time for modified film Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that the company incorporate the modification.