Twolevel Factorial Designs n Bacteria Example Response Bill

Two-level Factorial Designs n Bacteria Example: – Response: Bill length – Factors: § B: Bacteria (Myco, Control) § T: Room Temp (Warm, Cold) § I: Inoculation (Eggs, Chicks) Yandell, B. (2002) Practical Data Analysis for Designed Experiments, Chapman & Hall, London
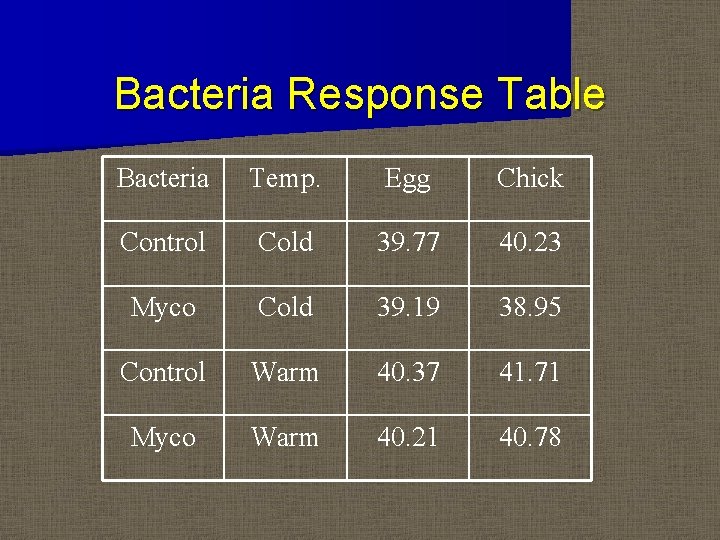
Bacteria Response Table Bacteria Temp. Egg Chick Control Cold 39. 77 40. 23 Myco Cold 39. 19 38. 95 Control Warm 40. 37 41. 71 Myco Warm 40. 21 40. 78
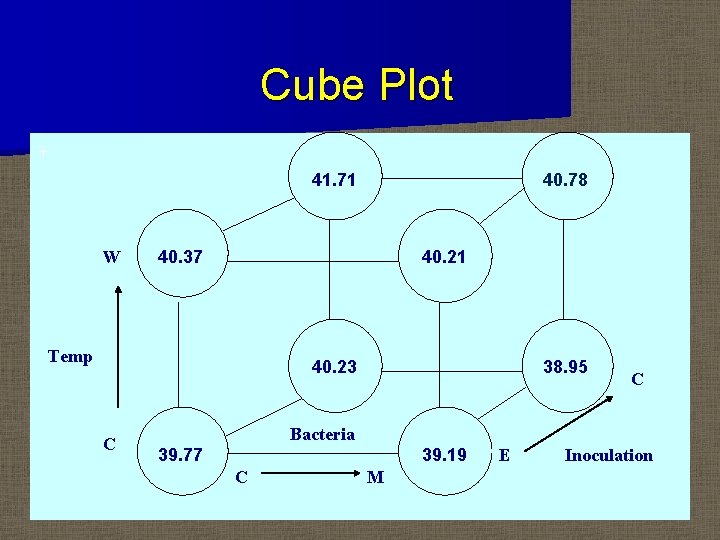
Cube Plot + 41. 71 W 40. 78 40. 37 40. 21 Temp 40. 23 C 38. 95 C Bacteria 39. 77 39. 19 C M E Inoculation

Cell Mean Estimates n For a k-factor design with n replicates, the cell means are estimated as n We can write any effect as a contrast; interaction contrasts are obtained by element-wise multiplication of main effect contrast coefficients.

Cell Mean Contrast Properties n The resulting contrasts are mutually orthogonal. n The contrasts (up to a scaling constant) can be summarized as a table of ± 1’s.

Orthogonal Contrast Coefficients

Estimated Effects n If we code contrast coefficients as ± 1, the estimated effects are: n These effects are twice the size of our usual ANOVA effects.

Sum of Squares n The sum of squares for the estimated effect can be computed using the sum of squares formula we learned for contrasts

SS Example n Bacteria Example B effect=(39. 19+38. 95+40. 21+40. 78 -39. 7740. 23 -40. 37 -41. 71)/4 =-. 7375 SSB=(-. 7375)2 x 2=1. 088 n The entire ANOVA table for this example can be constructed in this way
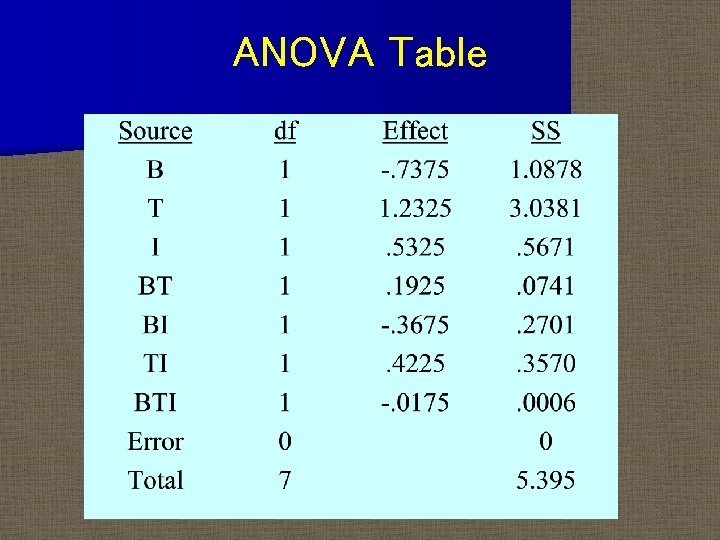
ANOVA Table

Testing Effects n With replication (n>1) n Without replication (k large) – Claim higher-order interactions are negligible and pool them – For k=6, if 3 -way (and higher) interactions are negligible, 42 d. f. would be available for error

Testing Without Replication n Without replication--Normal Probability Plots – If none of the effects is significant, the effects are orthogonal normal random variables with mean 0 and variance

Normal Probability Plots n Because the effects are normal, they are also independent n IID normal effects can be “tested” using a normal probability plot (Minitab Example) n Yandell uses a half-normal plot n You can pool values on the line as error and construct an ANOVA table

Lenth’s Test n Lenth (1989) developed a more formal test of effects. n Denote the effects by ei, i=1, …, m (m=2 k-1 for 2 k designs). n We say that the ei’s are iid N(0, t 2), where t is their common standard error.

Experimental Error Estimates n Lenth develops two estimates of the common standard error, t, of the ei’s:

Margins of Error n Though both are consistent estimates, PSE is more robust n The following terms (margins of error) are used to test effects

Testing with Margins of Error n The df term was developed from a study of the empirical distribution of PSE 2 n ME is a 1 -a confidence bound for the absolute value of a single effect n SME is an exact (since the effects are independent) simultaneous 1 -a confidence bound for all m effects
- Slides: 17