TwoDimensional Viewing Window A worldcoordinate area selected for

Two-Dimensional Viewing

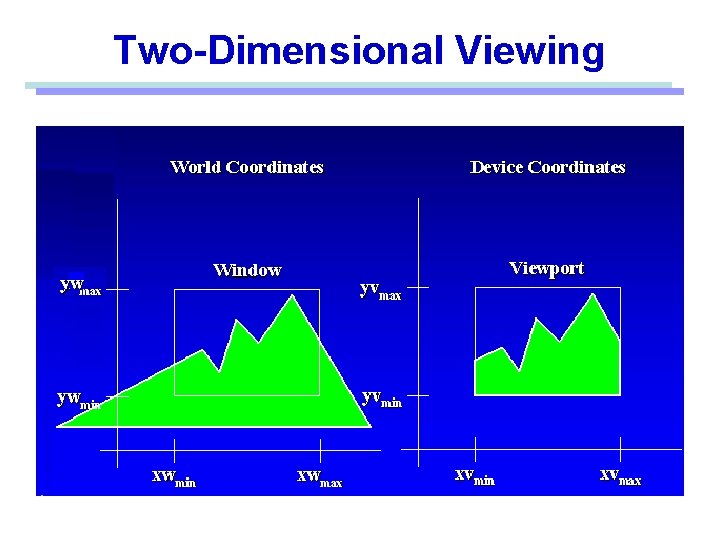
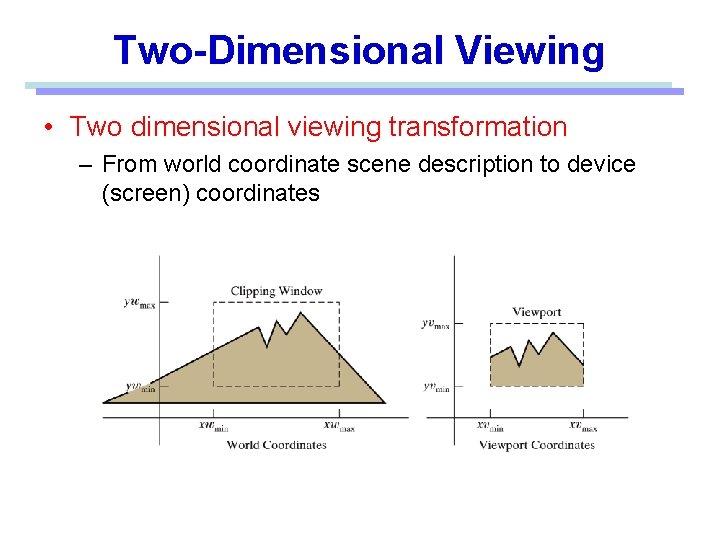
Window • A world-coordinate area selected for display. defines what is to be viewed Viewport • An area on a display device to which a window is mapped. defines where it is to be displayed Viewing transformation • The mapping of a part of a world-coordinate scene to device coordinates. A window could be a rectangle to have any orientation.

Two-Dimensional Viewing

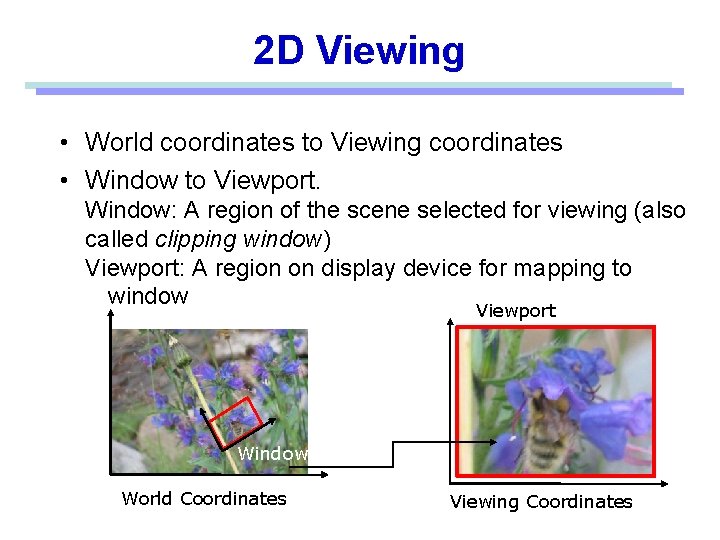
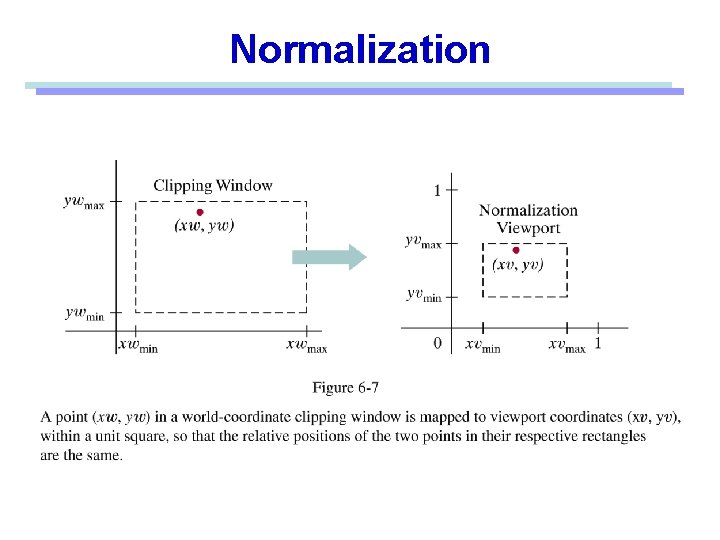
2 D Viewing • World coordinates to Viewing coordinates • Window to Viewport. Window: A region of the scene selected for viewing (also called clipping window) Viewport: A region on display device for mapping to window Viewport Window World Coordinates Viewing Coordinates

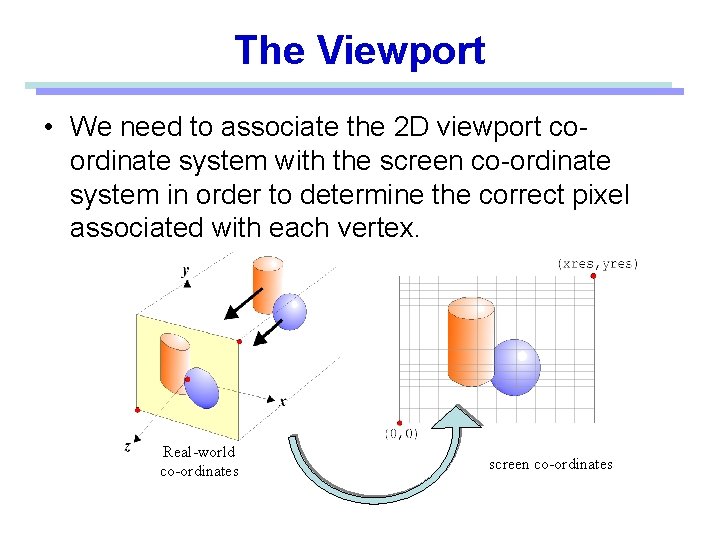
The Viewport • We need to associate the 2 D viewport coordinate system with the screen co-ordinate system in order to determine the correct pixel associated with each vertex. Real-world co-ordinates screen co-ordinates

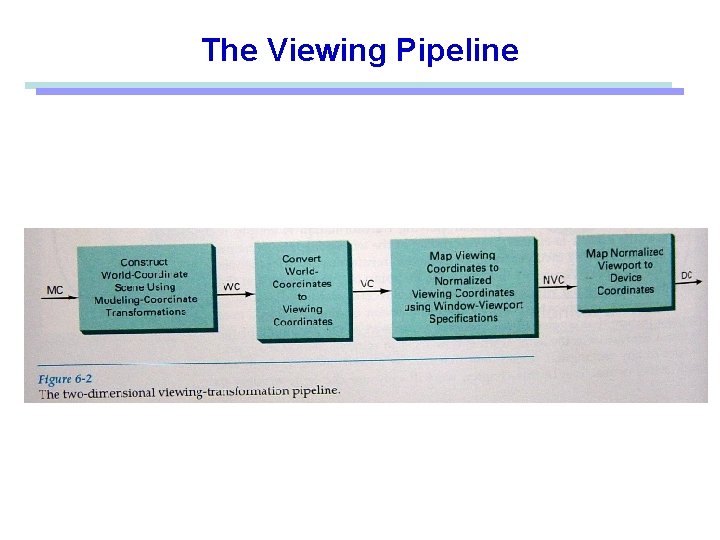
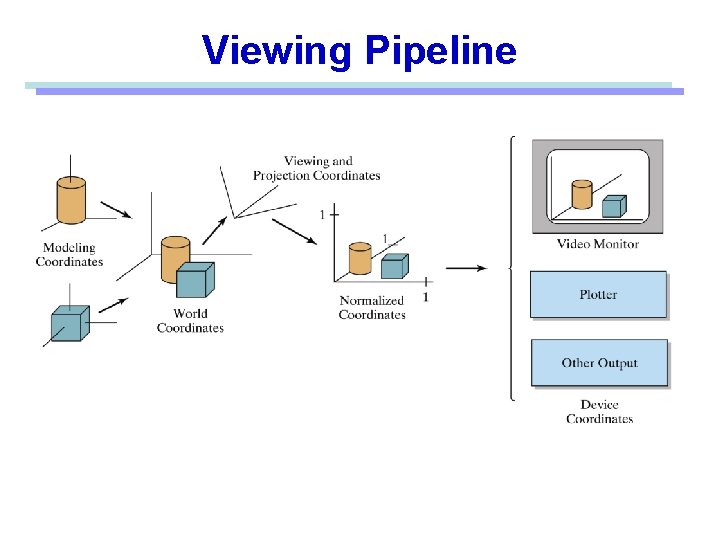
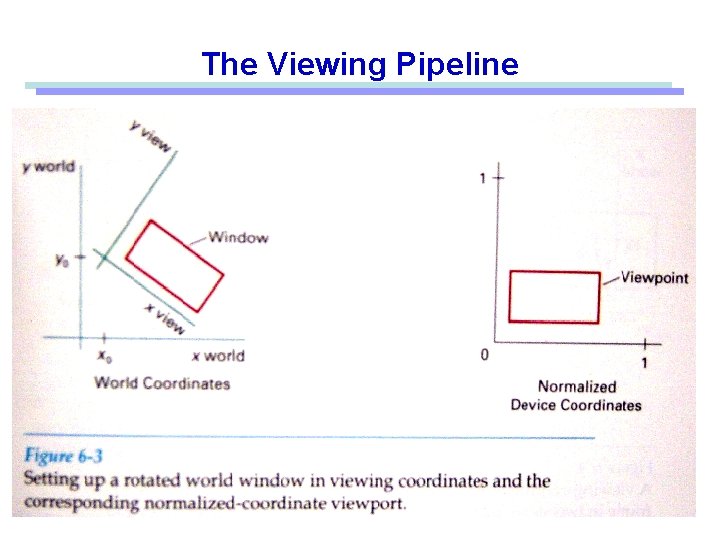
The Viewing Pipeline

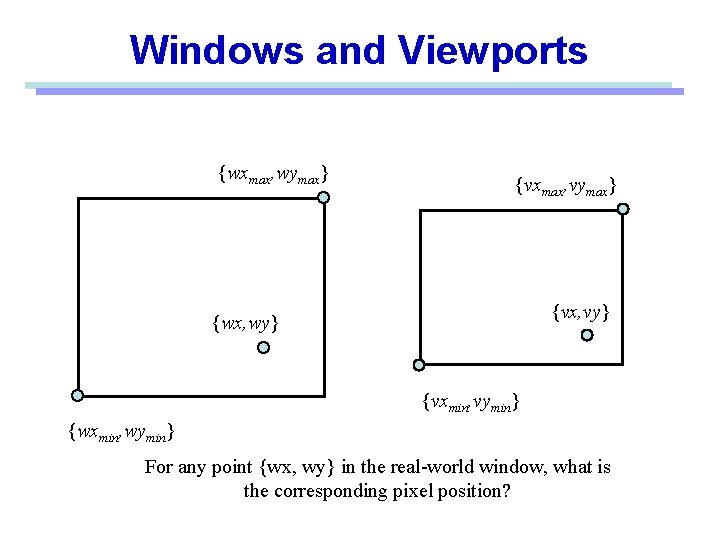
Windows and Viewports {wxmax, wymax} {vxmax, vymax} {vx, vy} {wx, wy} {vxmin, vymin} {wxmin, wymin} For any point {wx, wy} in the real-world window, what is the corresponding pixel position?

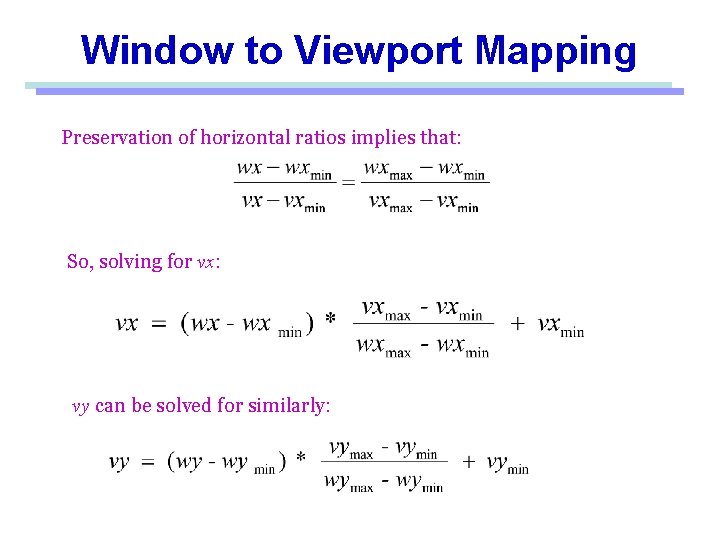
Window to Viewport Mapping Preservation of horizontal ratios implies that: So, solving for vx: vy can be solved for similarly:

Viewing Pipeline

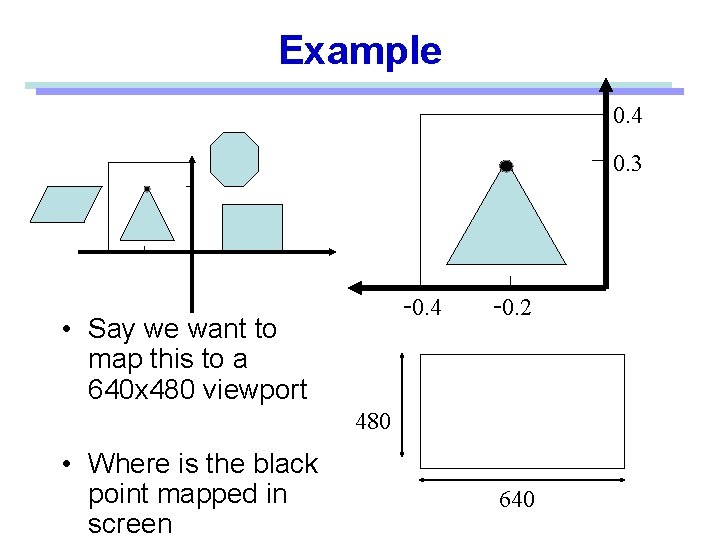
Example 0. 4 0. 3 -0. 4 • Say we want to map this to a 640 x 480 viewport -0. 2 480 • Where is the black point mapped in screen 640

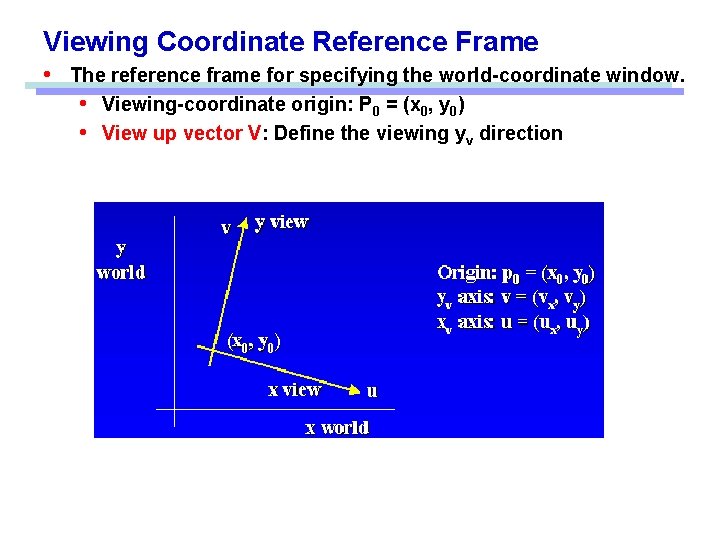
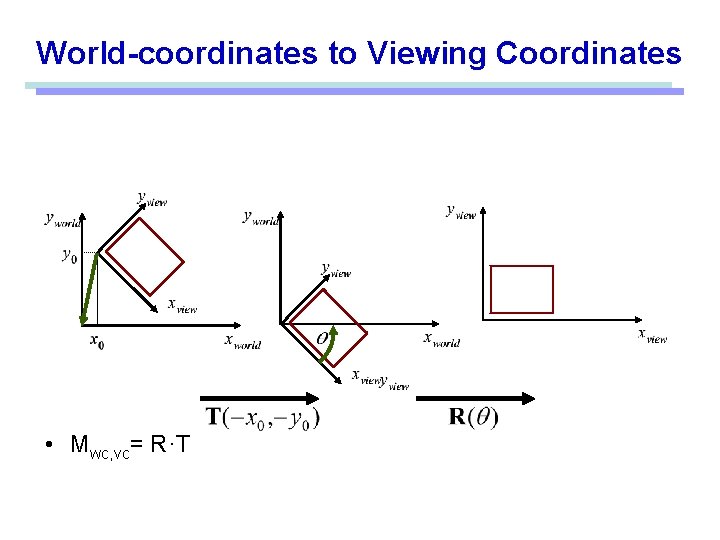
Viewing Coordinate Reference Frame • The reference frame for specifying the world-coordinate window. • Viewing-coordinate origin: P 0 = (x 0, y 0) • View up vector V: Define the viewing yv direction

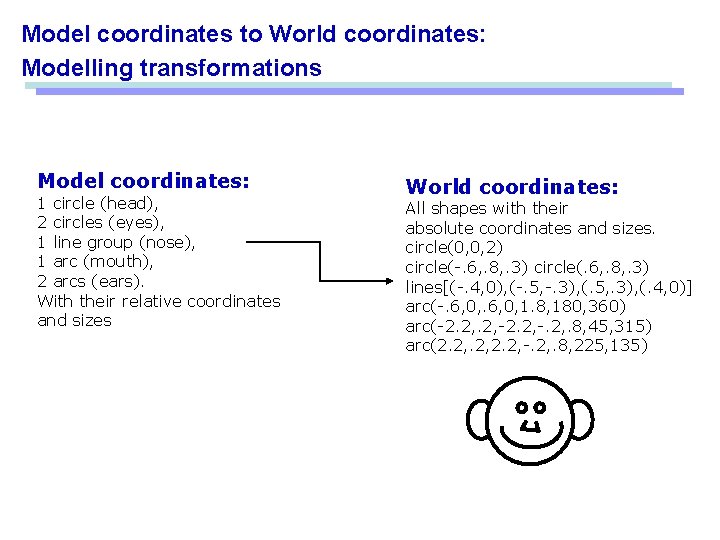
Model coordinates to World coordinates: Modelling transformations Model coordinates: 1 circle (head), 2 circles (eyes), 1 line group (nose), 1 arc (mouth), 2 arcs (ears). With their relative coordinates and sizes World coordinates: All shapes with their absolute coordinates and sizes. circle(0, 0, 2) circle(-. 6, . 8, . 3) circle(. 6, . 8, . 3) lines[(-. 4, 0), (-. 5, -. 3), (. 5, . 3), (. 4, 0)] arc(-. 6, 0, 1. 8, 180, 360) arc(-2. 2, -. 2, . 8, 45, 315) arc(2. 2, -. 2, . 8, 225, 135)

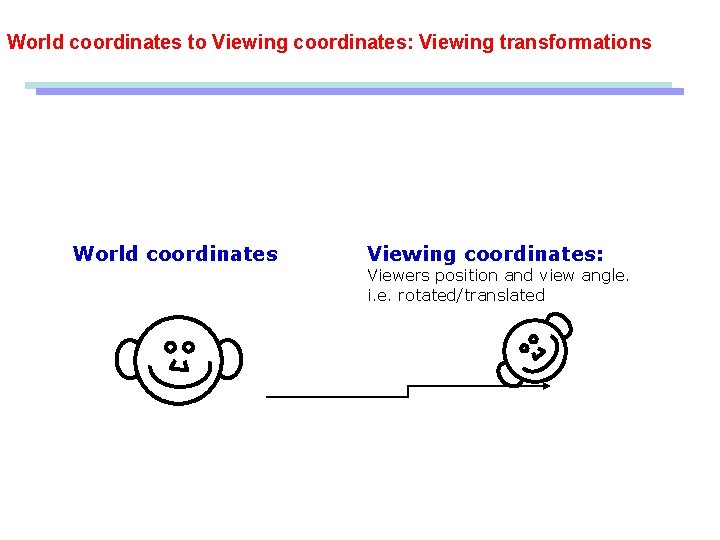
World coordinates to Viewing coordinates: Viewing transformations World coordinates Viewing coordinates: Viewers position and view angle. i. e. rotated/translated

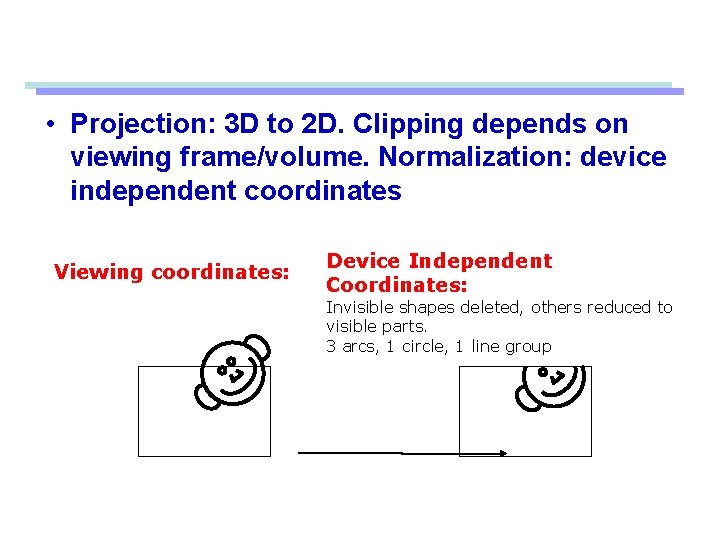
• Projection: 3 D to 2 D. Clipping depends on viewing frame/volume. Normalization: device independent coordinates Viewing coordinates: Device Independent Coordinates: Invisible shapes deleted, others reduced to visible parts. 3 arcs, 1 circle, 1 line group

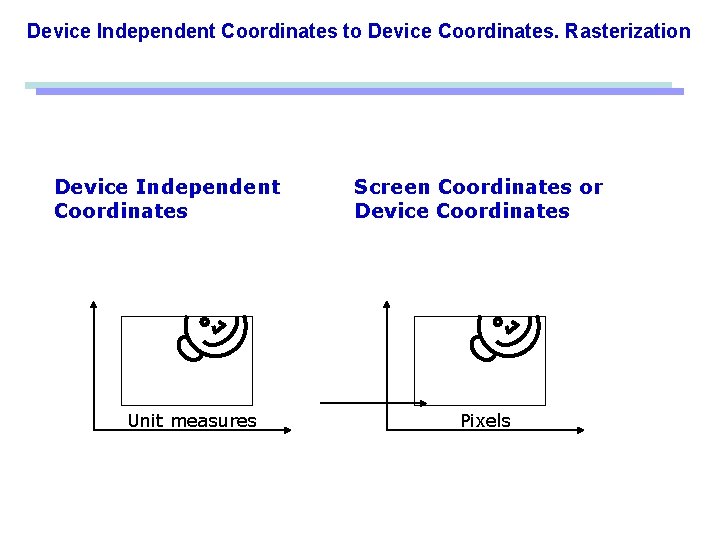
Device Independent Coordinates to Device Coordinates. Rasterization Device Independent Coordinates Unit measures Screen Coordinates or Device Coordinates Pixels

The Viewing Pipeline

World-coordinates to Viewing Coordinates • Mwc, vc= R·T

Two-Dimensional Viewing • Two dimensional viewing transformation – From world coordinate scene description to device (screen) coordinates

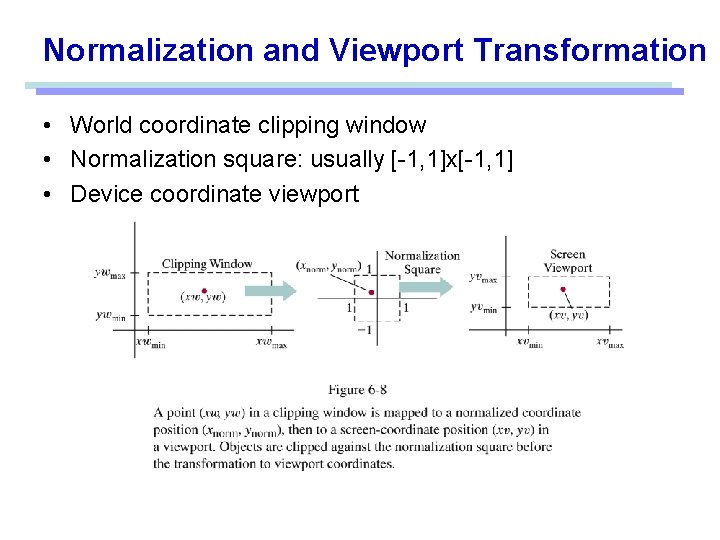
Normalization and Viewport Transformation • World coordinate clipping window • Normalization square: usually [-1, 1]x[-1, 1] • Device coordinate viewport

Normalization

Clipping • Remove portion of output primitives outside clipping window • Clipping • Identify those portions of a picture that are either inside or outside of a specified region of space. • Clip window • The region against which an object is to be clipped. • The shape of clip window • Two approaches – Clip during scan conversion: Per-pixel bounds check – Clip analytically, then scan-convert the modified primitives

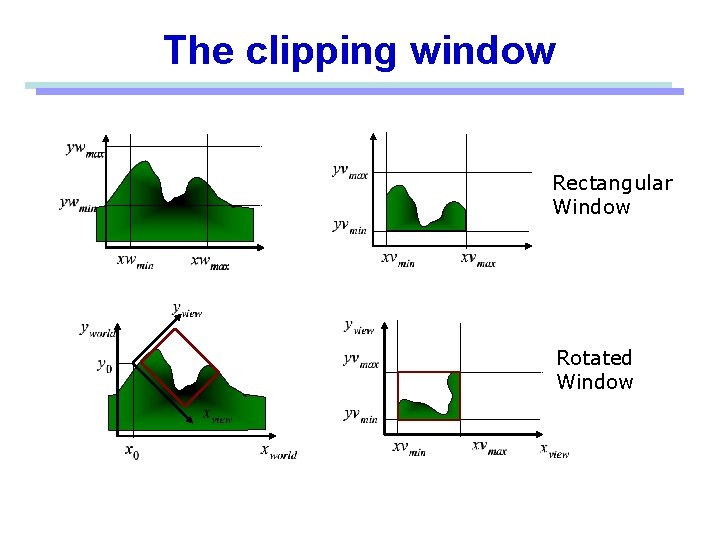
Clipping Window vs. Viewport • The clipping window selects what we want to see in our virtual 2 D world. • The viewport indicates where it is to be viewed on the output device (or within the display window) • By default the viewport have the same location and dimensions of the GLUT display window you create – But it can be modified so that only a part of the display window is used for Open. GL display

The clipping window Rectangular Window Rotated Window

Two-Dimensional Clipping • Point clipping – trivial • Line clipping – Cohen-Sutherland • Fill-area clipping – Sutherland-Hodgeman • Curve clipping • Text clipping

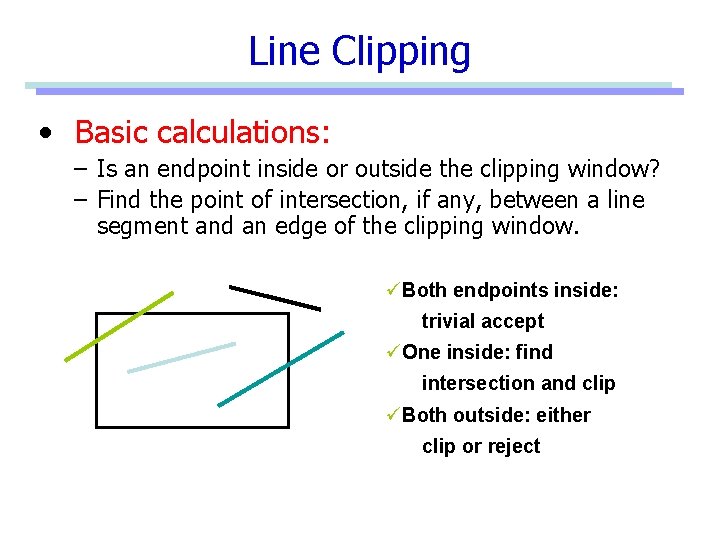
Line Clipping • Basic calculations: – Is an endpoint inside or outside the clipping window? – Find the point of intersection, if any, between a line segment and an edge of the clipping window. üBoth endpoints inside: trivial accept üOne inside: find intersection and clip üBoth outside: either clip or reject

Cohen-Sutherland Line Clipping • One of the earliest algorithms for fast line clipping • Identify trivial accepts and rejects by bit operations 1001 1000 1010 < Region code for each endpoint > Clipping window 0001 0000 0010 above below Bit 4 0101 0100 0110 3 right left 2 1

Cohen-Sutherland Line Clipping • • Compute region codes for two endpoints If (both codes = 0000 ) trivially accepted If (bitwise AND of both codes 0000) trivially rejected Otherwise, divide line into two segments – test intersection edges in a fixed order. (e. g. , top-to-bottom, right-to-left) 1001 1000 1010 Clipping window 0001 0000 0010 0101 0100 0110

Cohen-Sutherland Line Clipping • Fixed order testing and clipping cause needless clipping (external intersection)

Cohen-Sutherland Line Clipping • This algorithm can be very efficient if it can accept and reject primitives trivially – Clip window is much larger than scene data • Most primitives are accepted trivially – Clip window is much smaller than scene data • Most primitives are rejected trivially • Good for hardware implementation

Polygon Fill-Area Clipping • Polyline vs polygon fill-area • Early rejection is useful Bounding box of polygon fill area Clipping Window

Sutherland-Hodgman Polygon Clipping • Clip against 4 infinite clip edges in succession

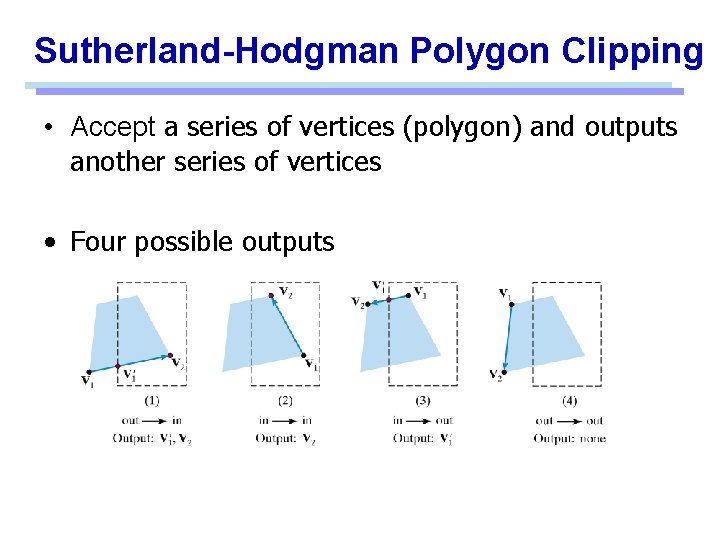
Sutherland-Hodgman Polygon Clipping • Accept a series of vertices (polygon) and outputs another series of vertices • Four possible outputs

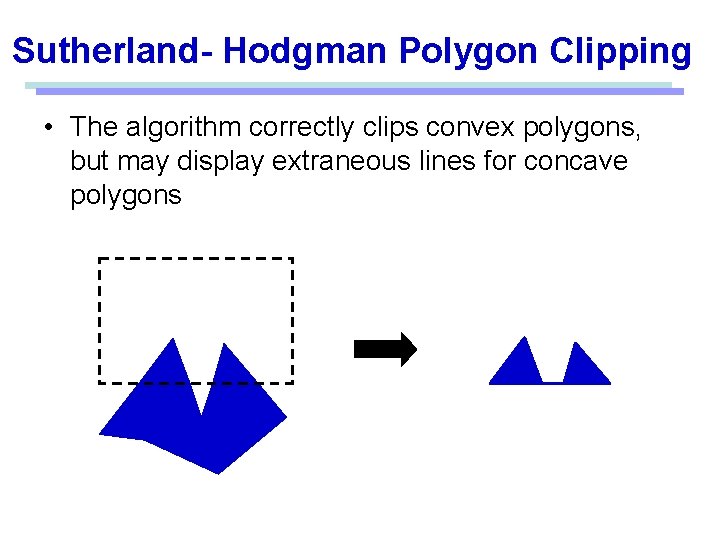
Sutherland- Hodgman Polygon Clipping • The algorithm correctly clips convex polygons, but may display extraneous lines for concave polygons

Other Clipping • Curve clipping • Use bounding rectangle to test for overlap with a rectangular clip window. • Text clipping • All-or-none string-clipping • All-or-none character-clipping • Clip the components of individual characters

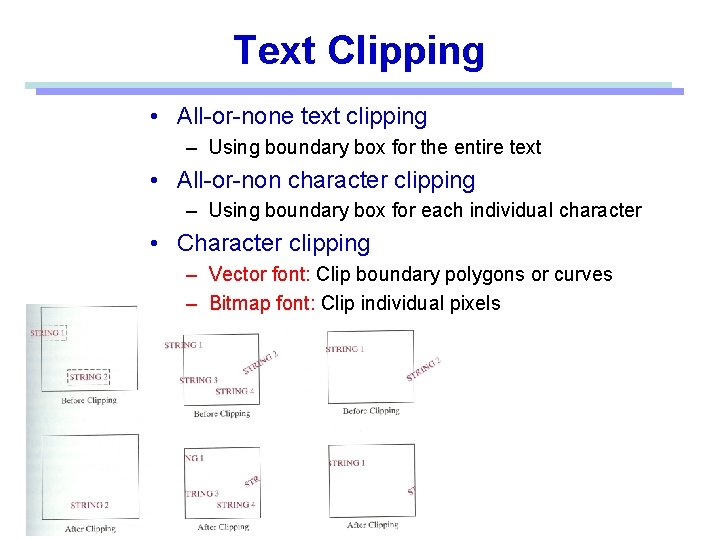
Text Clipping • All-or-none text clipping – Using boundary box for the entire text • All-or-non character clipping – Using boundary box for each individual character • Character clipping – Vector font: Clip boundary polygons or curves – Bitmap font: Clip individual pixels

Other Clipping Curve clipping • Use bounding rectangle to test for overlap with a rectangular clip window. Text clipping • All-or-none string-clipping • All-or-none character-clipping • Clip the components of individual characters

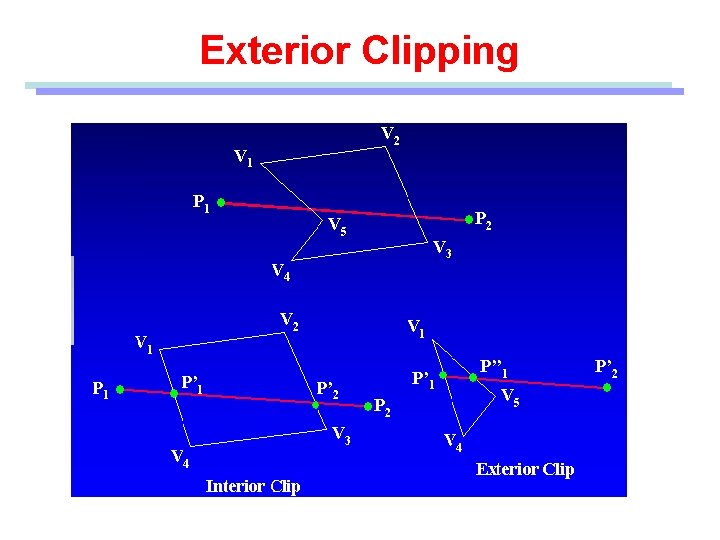
Exterior Clipping • Save the outside region • Applications • Multiple window systems • The design of page layouts in advertising or publishing Adding labels or design patterns to a picture • • Procedures for clipping objects to the interior of concave polygon windows

Exterior Clipping