Twoand ThreeDimentional Motion Kinematic Position Vector y C

Two-and Three-Dimentional Motion (Kinematic)

Position Vector y C The location of a particle relative to the origin of a coordinate system is given by a position vector r , which in unit – vector notation is A B x D Student Activity : State position points A, B, C, D using unit-vector notation.

Position as a function of time Example : Student Activity : Determine position of a particle that has function of time as stete above at : a. Initially b. t = 2 second c. t = 4 second

Displacement If a particle moves so that its position vector changes from particle’s displacement is The displacement can also be written as : to , the

Student Activity : Determine the displacement vector : a. From point A to point C b. b. From point A to point B The magnitude of displacement : y C A The direction of displacement is tate in angle : B x D

Student Activity Suppose the position vector of a particle is given by : t is in second and r in meter. Determine the magnitude and direction of particle displacement from t 1 = 1 s to t 2 = 2 s

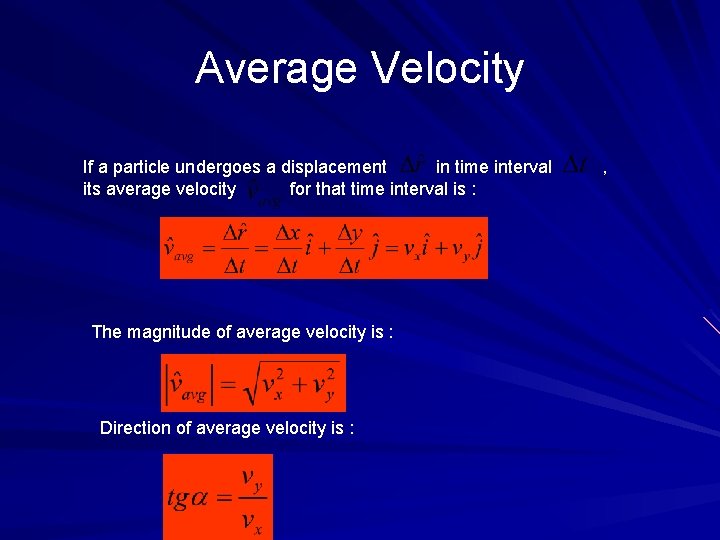
Average Velocity If a particle undergoes a displacement in time interval its average velocity for that time interval is : The magnitude of average velocity is : Direction of average velocity is : ,

Student Activity A particle is moving on an x-y coordinat plane. The change of particle position follows the equation : Where t is in second and r is in meter. Determine : a. Vector of average velocity if particle moves from t = 0 to t = 2 s b. Magnitude of average velocity from t = 0 to t = 2 s c. Direction of average velocity

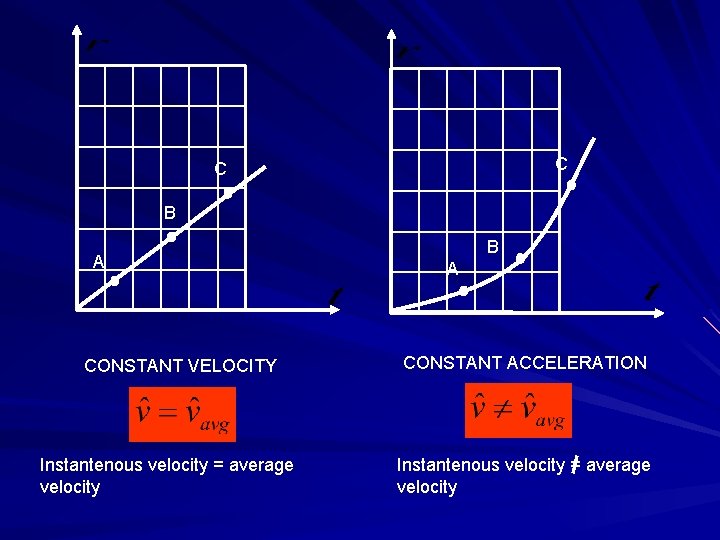
C C B A CONSTANT VELOCITY Instantenous velocity = average velocity B A CONSTANT ACCELERATION Instantenous velocity = average velocity

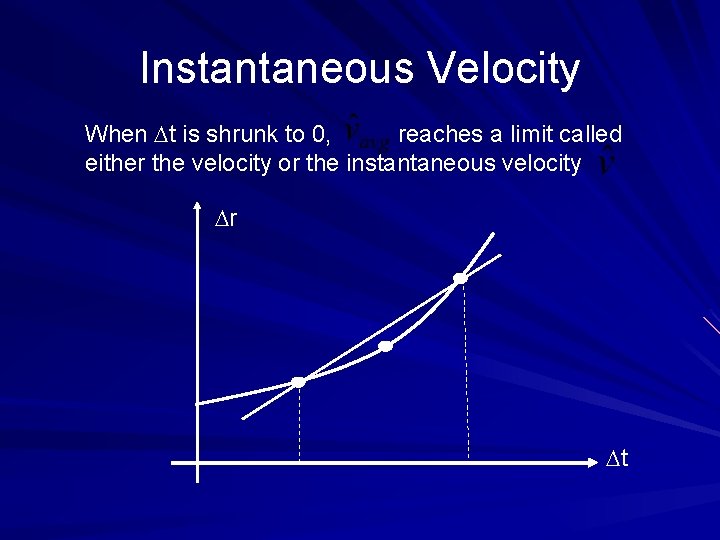
Instantaneous Velocity When Dt is shrunk to 0, reaches a limit called either the velocity or the instantaneous velocity Dr Dt

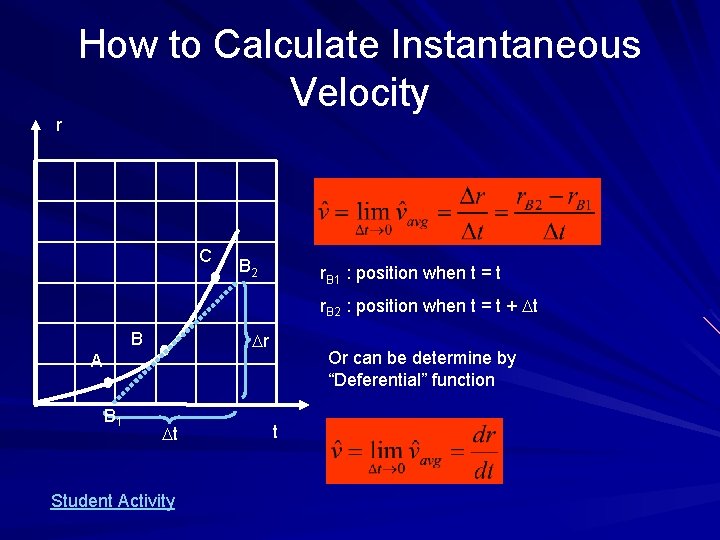
r How to Calculate Instantaneous Velocity C B 2 r. B 1 : position when t = t r. B 2 : position when t = t + Dt B Dr A B 1 Dt Student Activity Or can be determine by “Deferential” function t

Student Activity A particle is moving on an x-y coordinate plane. The change of particle position follows the equation Where t is in second and is in meter Determine : a. The vector instantaneous velocity at t = 2 s b. The magnitude and direction of instantaneous velocity at =2 s

Kerjakan soal berikut : Vektor posisi sebuah partikel yang bergerak dinyatakan oleh : r = 40 ti + (30 t-5 t 2)j a. Tentukan kecepatan dua detik pertama b. Tentukan kecepatan mula-mula c. Tentukan kecepatan saat t = 2 s

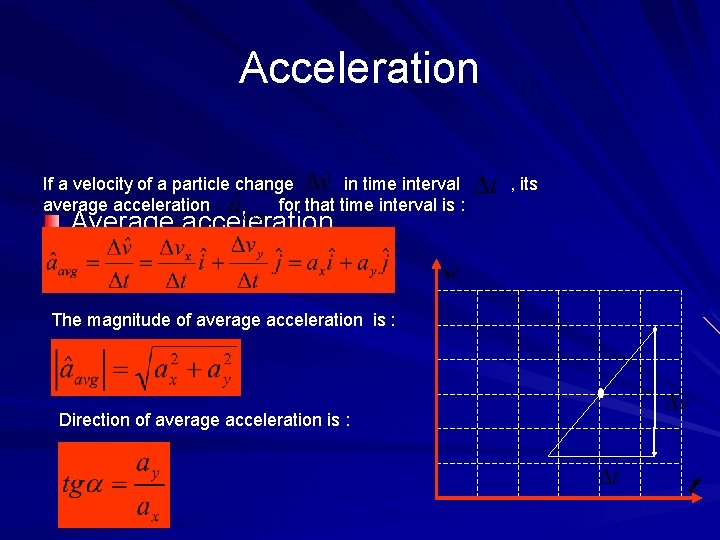
Acceleration If a velocity of a particle change in time interval average acceleration for that time interval is : Average acceleration The magnitude of average acceleration is : Direction of average acceleration is : , its

Student Activity The velocity equation of a moving particle is stated by : v = 4 ti + (10 + 0. 75 t 2)j Determine the average acceleration from t = 0 to t = 2 s

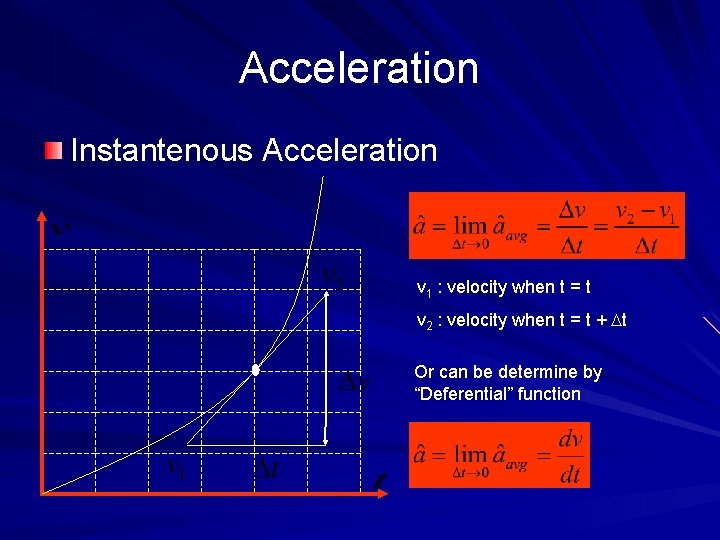
Acceleration Instantenous Acceleration v 1 : velocity when t = t v 2 : velocity when t = t + Dt Or can be determine by “Deferential” function

Student Activity A bird flying on the XY plane with velocity that is stated by : v = (2. 1 – 3. 6 t 2)i + 5. 0 tj. Initially the bird is on the (0; 0) Determine the vector of acceleration as time function Determine the bird acceleration at t = 2 s Determine the average acceleration in interval of time from t = 0 to t = 2 s

Determination velocity from acceleration equation To determine velocity from acceleration equation, we use integral function to change acceleration equation become velocity equation Integral Function to use Integral function in a simple way :

Student Activity A particle moves on the y axis with acceleration of a = 2 t , if initially its velocity is 3 m/s, determine the velocity at a. t = 2 s b. t = 4 s

Determination position from velocity equation To determine position from velocity equation, we use integral function to change velocity equation become position equation Integral Function to use Integral function in a simple way :

Percepatan gerak partikel dinyatakan dengan persamaan a = 2 ti + 4 j, a dlm m/s 2. jika mula-mula partikel beada di posisi 2 i + j, dalam keadaan diam, tentukan kecepatan dan posisinya saat t = 4 s.

Sebuah partikel P bergerak dengan percepatan a. Tentukan vektor kecepatan dan vektor posisi P pada saat t. jika diketahui a = 15 t 2 i + 8 tj. Mula-mula partikel di titik asal dan sedang bergerak dengan kecepatan i + 2 j

Kecepatan gerak partikel dinyatakan dalam persamaan : v = 3 t 2 i + 4 tj, mula partikel berada di posisi 3 j. Tentukan a. posisi partikel saat t = 3 s b. percepatan partikel saat t = 2 s

Selesai