Two Way Tables How they help theoretical probability

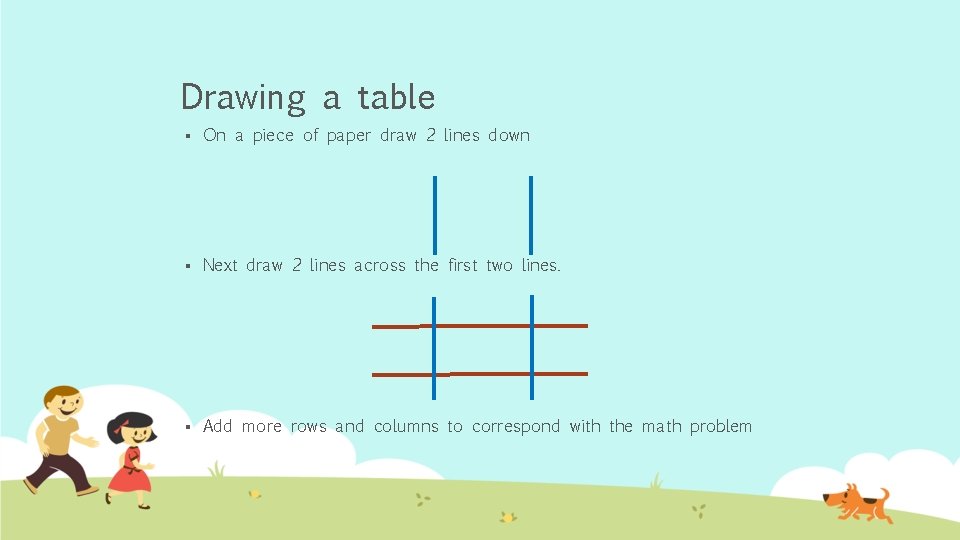
Drawing a table § On a piece of paper draw 2 lines down § Next draw 2 lines across the first two lines. § Add more rows and columns to correspond with the math problem

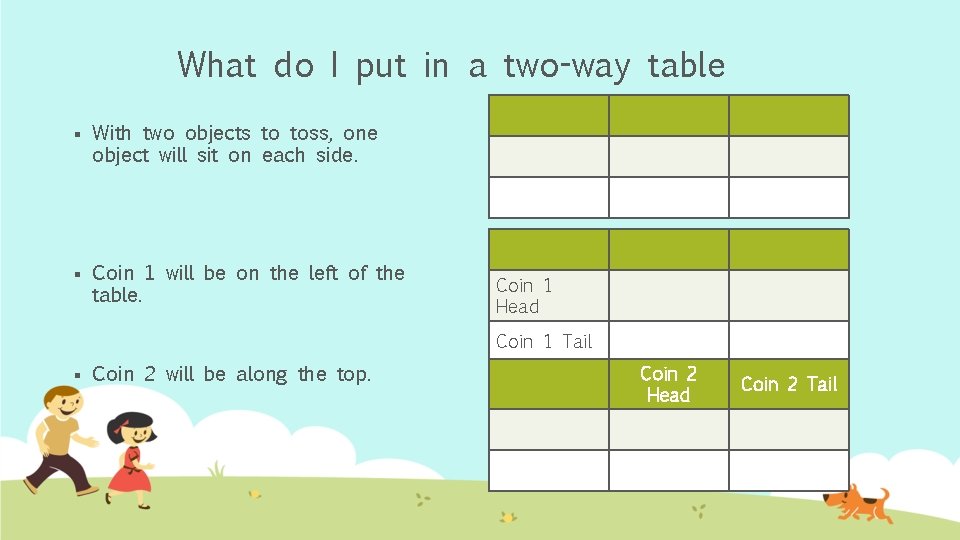
What do I put in a two-way table § With two objects to toss, one object will sit on each side. § Coin 1 will be on the left of the table. Coin 1 Head Coin 1 Tail § Coin 2 will be along the top. Coin 2 Head Coin 2 Tail

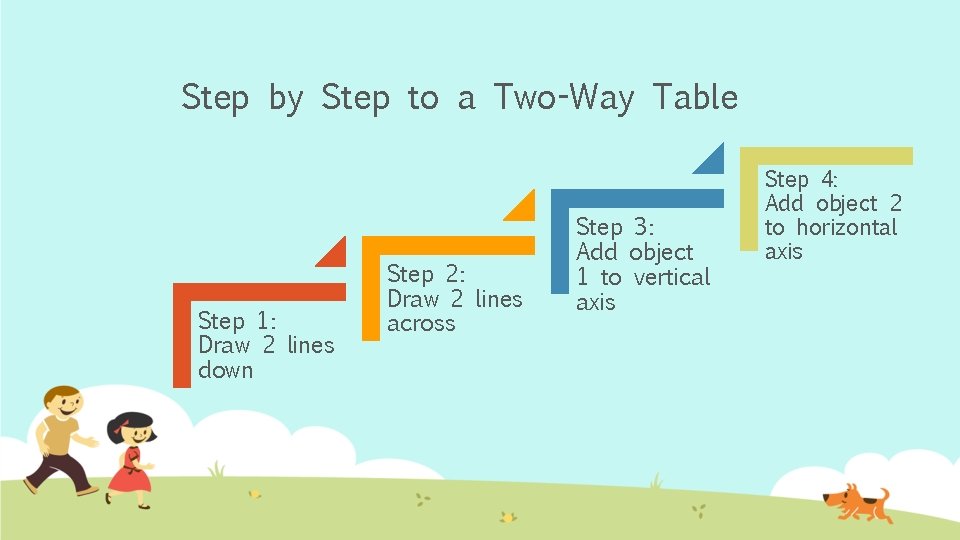
Step by Step to a Two-Way Table Step 1: Draw 2 lines down Step 2: Draw 2 lines across Step 3: Add object 1 to vertical axis Step 4: Add object 2 to horizontal axis

Inserting Possible Outcomes How to add theory

Coin Toss Table § To see what possible outcomes there are in a two coin toss we use both sides of the table to insert values. § Place the side value in first § Then add the top value for that column § We can now see there are 4 possible outcomes. HH, HT, TH, TT § Each outcome is worth ¼ Coin 2 Head Coin 2 Tail Coin 1 Head 1 H 2 H 1 H 2 T Coin 1 Tail 1 T 2 H 1 T 2 T

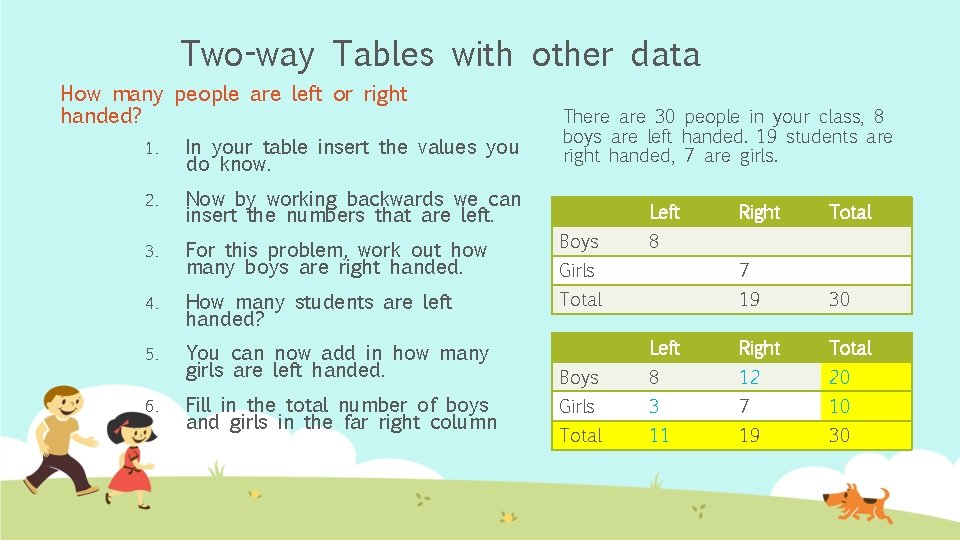
Two-way Tables with other data How many people are left or right handed? 1. In your table insert the values you do know. There are 30 people in your class, 8 boys are left handed. 19 students are right handed, 7 are girls. 2. Now by working backwards we can insert the numbers that are left. 3. For this problem, work out how many boys are right handed. Boys Girls 7 4. How many students are left handed? Total 19 30 5. You can now add in how many girls are left handed. Left Right Total Boys 8 12 20 Girls 3 7 10 Total 11 19 30 6. Fill in the total number of boys and girls in the far right column Left Right Total 8

Finding the Totals § § 1. To find the totals for the table you add the numbers from one row at a time. For this example: Add the boys row: left (8) + right (12) = 20. The total is 20 so that goes in the end column 2. Do the same for the girls row. 3. To find the total for the column add the figures going down: 4. 1. Left column: boys (8) + girls (3) = 11. The total column is 11. 2. Do the same for the ‘Right’ column The sum of the totals should be the same for the row and column. In this example, both equal 30. Left Right Total Boys 8 12 20 Girls 3 7 10 Total 11 19 30 Left Right Total Boys Girls Total 30

Left Right Total Boys 8 12 20 Girls 3 7 10 We can now see what the probability of choosing a boy who is left handed. There are 30 possibilities - the denominator. Total 11 19 30 There are 8 who are in the category we are trying to choose – the numerator. The probability is 8/30

Boys Left Right Total 8 12 20 Task 2: What is the probability of choosing: 1. A right handed girl? Girls 3 7 10 Total 11 19 30 2. A girl? 3. Someone who is left handed? Write down your answers, check in your pair.

What were your answers? 1. Probability of a right handed girl? 7/30 2. Probability of the student being a girl? 3. Probability of choosing someone left handed? 11/30 Do you have any questions? Please see your teacher for answers. 10/30 or 1/3