Two Sample T Test Why 2 samples Sometimes

Two Sample T Test

Why 2 samples? Sometimes we have two samples we wish to test ◦ Experimental vs. control group ◦ Two groups from a sample ◦ Democrats vs. republicans ◦ Males vs. females

Logic of Two Sample Tests Scenarios ◦ 2 populations: Simply compare the two means or proportions and discern any difference between the two groups. ◦ 1 Sample 1 population: We attempt to discern if there any differences between the sample and the populations. Comparing the sample mean with population mean provides some information. But there is always the possibility that the sample and population are different just by chance. ◦ 2 samples: We attempt to discern if there any differences between the underlying populations. Comparing the sample means provides some information. But there is always the possibility that the two samples are different just by chance. 3

Logic of Two Sample Tests The differences between two samples from the same population have a sampling distribution, just as we have encountered the normal distribution and the distribution of sampling means. Follows a T distribution Knowledge of this distribution allows us to make inferences What is the probability of drawing two samples with a certain difference between them? 4

Logic of 2 Sample Tests If the two samples are fairly similar (taking into consideration their dispersion and the sample size), we will most likely conclude they are from the same underlying population. If the two samples are different and the probability of observing such a difference when the two samples are really from the same underlying population is fairly low, say 5% or lower, we will conclude that the samples are drawn from two different populations. 5

Family of T-tests Independent samples are composed of groups that are in no way matched to each other. A common example would be when samples are drawn from different populations. 1. 2. Homogenous variances Unequal Variances Dependent Samples 6

Family of t-tests If the two variances are the same we estimate a pooled estimate of common variance which is a weighted average of the variances from the two samples. If the two variances are different, we must use a different formula for estimating the standard error. 7

Two Independent samples t-test 8

Standard error for Two independent samples t-test 9

d. f. for Two independent samples 10

F-test How do we know if the population variances are the same? We use an F test for homogeneity of variances. The F test is another test of statistical significance. Here the hypothesis is that the two populations have equal variances. The formula for the f test: 11

F-Test for homogenous variances with df = nlarger – 1 for the numerator and nsmaller -1 for the denominator. 12

Equal Variance T-statistic If the F-test indicates equal variances, we make use of the following t-statistic: df = n 1+n 2 -2 13

Properties of T-Statistic Properties of T statistic: Like other tests of statistical significance, the larger t is, the more likely the difference is statistically significant. What happens to T as n 1 or n 2 gets larger? What happens to T as s 1 or s 2 gets larger? What happens to T as the difference between the two sample means grows? 14

Two Sample T-statistic The T statistic is a function of: 1. The sample sizes – This suggests you attempt to have the largest samples possible in any study. 2. The magnitude of the differences between the groups. 3. The amount of dispersion in the samples. 15

Examples What are some hypotheses from the article on rent control? How might you test these hypotheses? 16

Examples New York City is an example of a natural experiment ◦ Buildings built after 1974 exempt from rent regulation 17

Examples What are some hypotheses from the articles on rent control? ◦ ◦ Does rent control inhibit mobility? Does rent control benefit low income households? Does rent control encourage people to consume “too much” housing? Are rent controlled units in worse condition? 18

Summary of Two Sample T-Test for Independent Samples 1. Formulate H 0 and H 1 for comparison of two means. 2. State 3. For each sample calculate n, s 1, s 2 and s. e. 1 and s. e. 2 19

Summary of Two Sample T-Test for Independent Samples 4. Determine if t-test for equal variances can be used by performing F test for homogenous variances. ◦ a. Formulate H 0 and H 1 for comparison of two variances. ◦ b. State ◦ c. Calculate F ◦ d. If Fobtained does not exceed Fcritical, assume equal variances and use equal variance t-test. Otherwise unequal variance ttest. ◦ Note: If you have a large sample (>50) you don’t have to worry so much about variances 5. Conduct appropriate t-test. 20

Dependent Samples A dependent sample is one where the two groups are formed from matched pairs. Examples: A study that compared sets of identical twins. In this case, each sample is made up of twins who have a counterpart in the other sample. 21

Family of T-tests Matched Pairs Examples continued – Another common use of dependent samples is for “before and after comparisons. ” Each observation is measured before some treatment and then again after the treatment. Each item in the before sample thus has a corresponding match in the after sample. 22

Dependent Sample T-test The t-test can also be adapted to test for significant differences between matched pairs. It is often impractical to assign individuals to treatment and control groups. In such cases before and after comparisons on the same individuals might be more appropriate. 23

Dependent Sample T-test The logic of the dependent samples t-test is similar to that for the independent samples t-test. We wish to determine if the differences between the pairs is large and consistent enough to conclude that there really is a difference between these pairs in the population. 24

Dependent Sample T-test df = np-1 25

Dependent Sample t-statistic D is the mean of all the differences between the matched pairs in the sample. SD is the sample standard deviation of the difference scores: np is the number of pairs 26

Dependent Sample standard deviation 27

Dependent Sample t-statistic 1. As D gets larger the difference between pairs is more likely to be statistically significant. 2. As n gets larger the difference between pairs is more likely to be statistically significant. The less dispersion there is in the sample the difference between pairs is more likely to be statistically significant. 28

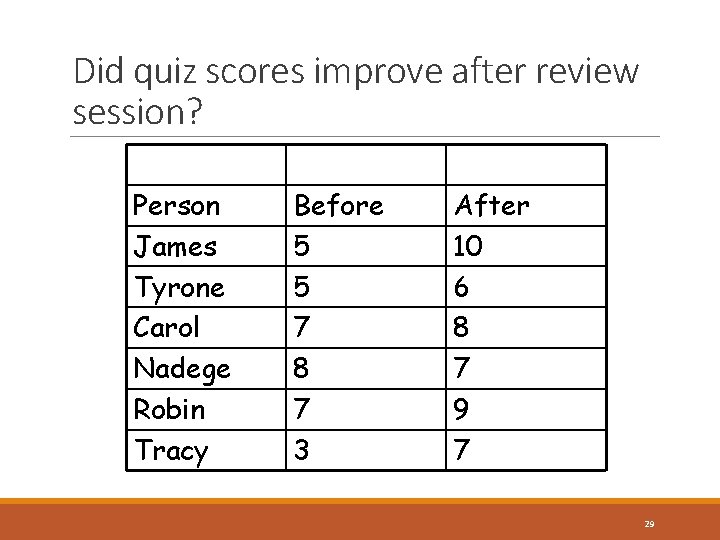
Did quiz scores improve after review session? Person James Tyrone Carol Nadege Robin Tracy Before 5 5 7 8 7 3 After 10 6 8 7 9 7 29

Example H 0: d = 0 H 1: > 0 : . 01 one tail SD = 2 np = 6 df = np-1 tobtained = 2. 236 tcritical = 3. 365 Cannot reject the null hypothesis 30

2 Sample. T-Test for proportions Analogous to 2 sample ttest for means 31

2 Sample. T-Test for proportions 32

2 Sample t-test proportion Stata example

Conclusion Hypothesis testing is an integral part of the research process. The t-statistic is a versatile tool for testing differences between groups. In addition to considering statistical significance, the more subjective test of research significance must be considered too. 34