Two Sample t procedures Difference of means Independent

Two Sample t procedures

Difference of means Independent samples consist of two groups of individuals who are randomly selected from two different populations. Both populations are Normally distributed. The means and standard deviations of the populations are unknown. In practice, it is enough that the distributions have similar shapes and that the data have no strong outliers

Paired t Interval for Population Means (when σ is unknown)

Degrees of Freedom There are two ways of computing degrees of freedom: 1) 2) Use technology. Use the degrees of freedom that is the smallest (from the smaller sample size).

Standard deviation means and proportions

Practice It!!!! It has been questioned many times whether or not individuals are dependent on caffeine to wake up in the morning. Eleven individuals were tested and their energy levels were measured. The first week of the trial they continued with their morning coffee. Their average energy level score was 15. 93 with a standard deviation 4. 1. The second week of the trial they had no coffee. Their average energy level score was 9. 48 with a standard deviation 3. 2. Find the 90% confidence interval for the mean change in energy level score.

Mean difference When studying paired samples means, we are told we are looking at the "mean difference”, this is not the same as the “difference of means”. This is calculated by taking the difference between each pair in the data, and then taking the mean of all those differences. Then constructing a C. I. from that data. We are changing the 2 data sets into a single data set.

Possibilities for comparison for both cases. Population one is less than the other, meaning a negative difference ( Left tail) Population one is greater than the other, meaning a positive difference(Right Tail) Population one is not the same as the other, meaning any significant difference. (Two tail)

Summary To figure out our what to do we need to ask ourselves a few questions. 1) Is the parameter of interest a mean or proportion ? 2) Is standard deviation know or unknown? 3) Is it one sample, or comparing two samples?

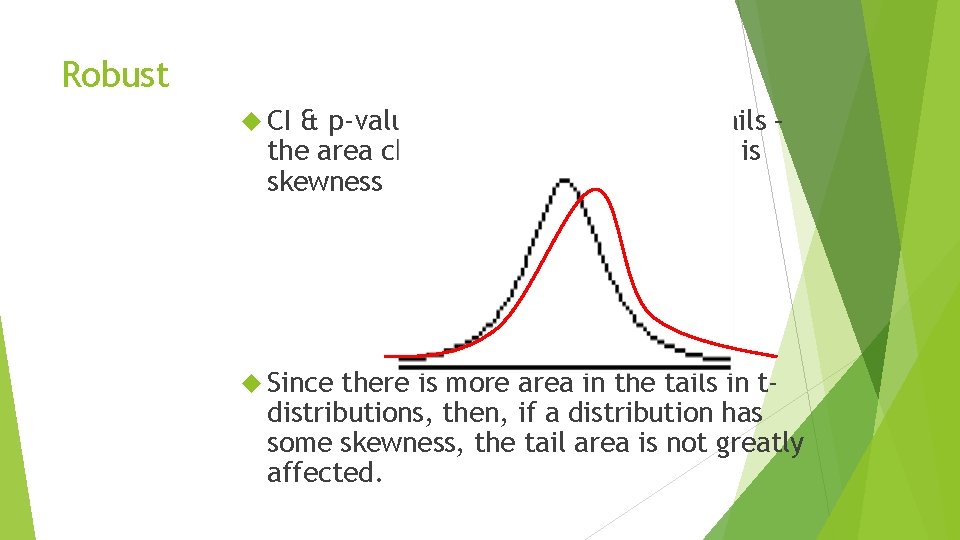
Robust An inference procedure is ROBUST if the confidence level or p-value doesn’t change much if the assumptions are violated. t-procedures can be used with some skewness, as long as there are no outliers. Larger n can have more skewness

Robust CI & p-values deal with area in the tails – the area changed greatly when there is skewness Since there is more area in the tails in tdistributions, then, if a distribution has some skewness, the tail area is not greatly affected.