Two Sample Hypothesis Testing for Proportions 2010 Pearson

Two Sample Hypothesis Testing for Proportions © 2010 Pearson Prentice Hall. All rights reserved

Sampling Distribution of the Difference between Two Proportions Suppose that a simple random sample of size n 1 is taken from a population where x 1 of the individuals have a specified characteristic, and a simple random sample of size n 2 is independently taken from a different population where x 2 of the individuals have a specified characteristic. The sampling distribution of , where and , is approximately normal, with mean and standard deviation provided that 11 -2 and .

Sampling Distribution of the Difference between Two Proportions The standardized version of is then written as which has an approximate standard normal distribution. 11 -3

The best point estimate of p is called the pooled estimate of p, denoted , where Test statistic for Comparing Two Population Proportions 11 -4

Hypothesis Test Regarding the Difference between Two Population Proportions To test hypotheses regarding two population proportions, p 1 and p 2, we can use the steps that follow, provided that: 1. the samples are independently obtained using simple random sampling, 2. and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. 11 -5

Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways: 11 -6

Step 2: Select a level of significance, , based on the seriousness of making a Type I error. 11 -7

Step 3: Compute the test statistic where 11 -8

P-Value Approach Step 4: Use Table V to estimate the P-value. . 11 -9

P-Value Approach Two-Tailed 11 -10

P-Value Approach Left-Tailed 11 -11

P-Value Approach Right-Tailed 11 -12

P-Value Approach Step 5: If the P-value < , reject the null hypothesis. If the P-value ≥ α, fail to reject the null hypothesis 10 -13

Step 6: State the conclusion in the context of the problem. 10 -14

Parallel Example 1: Testing Hypotheses Regarding Two Population Proportions An economist believes that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. He obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Test the economist’s claim at the =0. 05 level of significance. 11 -15

Solution We must first verify that the requirements are satisfied: 1. The samples are simple random samples that were obtained independently. 2. x 1=338, n 1=800, x 2=292 and n 2=750, so 3. The sample sizes are less than 5% of the population size. 11 -16

Solution Step 1: We want to determine whether the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. So, H 0: p 1 = p 2 versus H 1 : p 1 > p 2 or, equivalently, H 0: p 1 - p 2=0 versus H 1 : p 1 - p 2 > 0 Step 2: The level of significance is = 0. 05. 11 -17

Solution Step 3: The pooled estimate of The test statistic is: 11 -18 is:

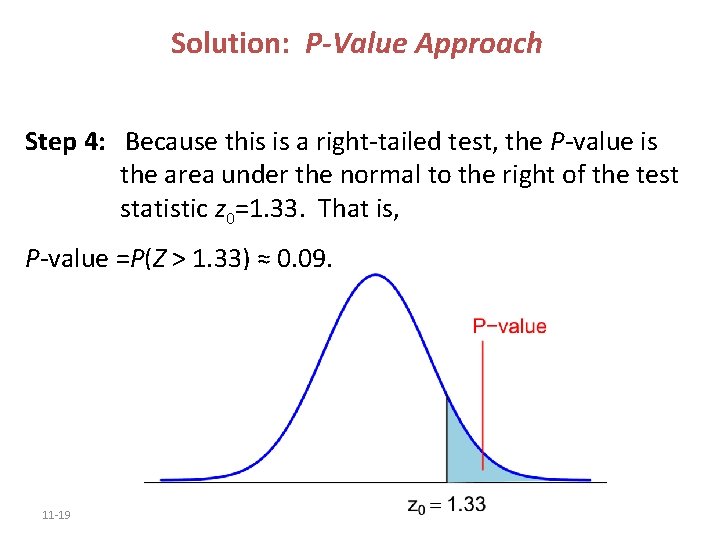
Solution: P-Value Approach Step 4: Because this is a right-tailed test, the P-value is the area under the normal to the right of the test statistic z 0=1. 33. That is, P-value =P(Z > 1. 33) ≈ 0. 09. 11 -19

Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance =0. 05, we fail to reject the null hypothesis. 11 -20

Solution Step 6: There is insufficient evidence at the =0. 05 level to conclude that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. 11 -21

Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions To construct a (1 - ) 100% confidence interval for the difference between two population proportions, the following requirements must be satisfied: 1. the samples are obtained independently using simple random sampling, 2. , and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. 11 -22

Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions Provided that these requirements are met, a (1 - ) 100% confidence interval for p 1 -p 2 is given by Lower bound: Upper bound: 11 -23

Parallel Example 3: Constructing a Confidence Interval for the Difference between Two Population Proportions An economist obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Find a 99% confidence interval for the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access. 11 -24

Solution We have already verified the requirements for constructing a confidence interval for the difference between two population proportions in the previous example. Recall 11 -25

Solution Thus, Lower bound = Upper bound = 11 -26

Solution We are 99% confident that the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access is between -0. 03 and 0. 10. Since the confidence interval contains 0, we are unable to conclude that the proportion of urban households with Internet access is greater than the proportion of rural households with Internet access. 11 -27