Two dimensional viewing Mechanism for displaying views of

Two dimensional viewing Mechanism for displaying views of a picture on the o/p device • Windowing Concepts • Clipping – Introduction – Point clipping – Line Clipping • Cohen-Sutherland Clipping Algorithm – Polygon Clipping • Sutherland-Hodgeman Area Clipping Algorithm

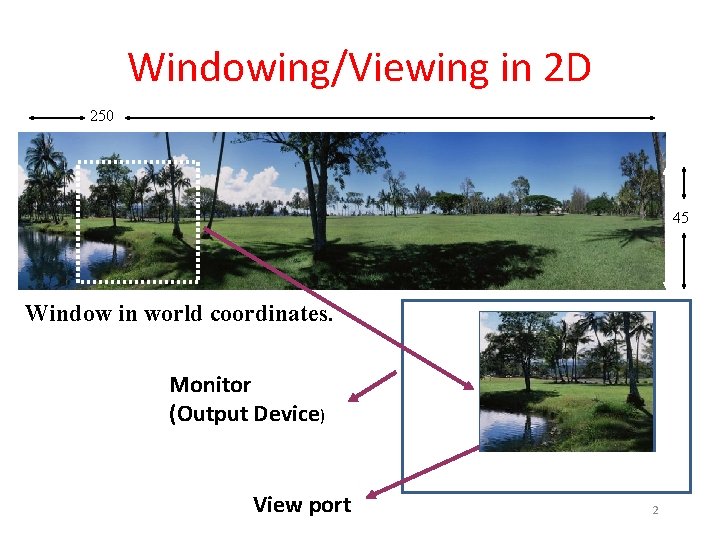
Windowing/Viewing in 2 D 250 45 Window in world coordinates. Monitor (Output Device) View port 2

Windowing Pipeline Window -- A world coordinate selected for displaying View Port – An area on a display device to which a window is mapped The window defines what to be viewed, the viewport defines where to be displayed The mapping of window to viewport is called • Windowing Transformation • Viewing Transformation • Window to viewport Transformation

Clipping Window & Viewport

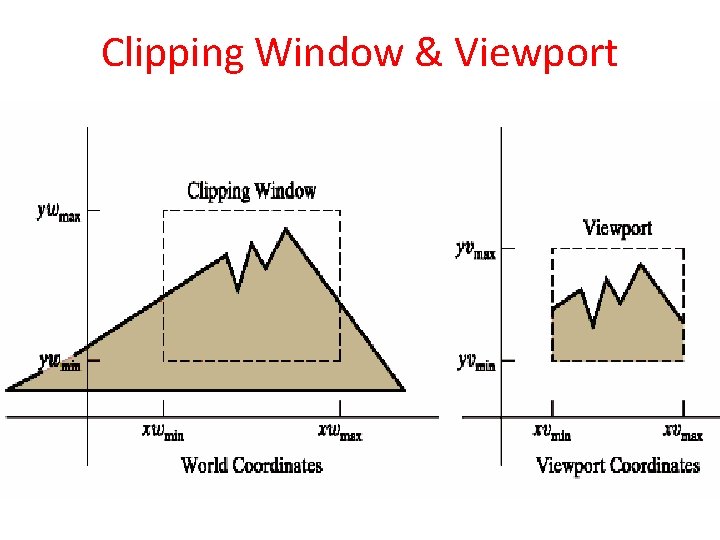
Mapping of point (Xw, Yw) of window to point (Xv, Yv) of viewport To maintain the relative placement of the point

Mapping Equation Where If Sx = Sy then relative proportion of the object’s are maintained else object will stretched or contracted in either X/Y direction

Clipping Any procedure that identifies those portion of a picture that are inside or outside is called as clipping • Point Clipping • Line Clipping • Polygon Clipping

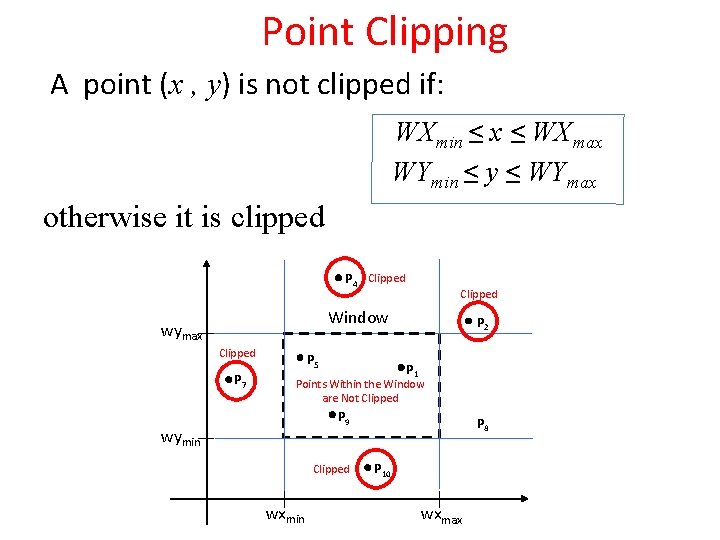
Point Clipping A point (x , y) is not clipped if: WXmin ≤ x ≤ WXmax WYmin ≤ y ≤ WYmax otherwise it is clipped P 4 Clipped Window wymax Clipped P 7 P 5 P 2 P 1 Points Within the Window are Not Clipped P 9 wymin Clipped wxmin P 8 P 10 wxmax

Line Clipping • For the image below consider which lines should be kept and which ones should be clipped P 4 Window wymax P 6 P 3 P 1 P 5 P 7 P 9 P 8 wymin P 10 wxmin wxmax

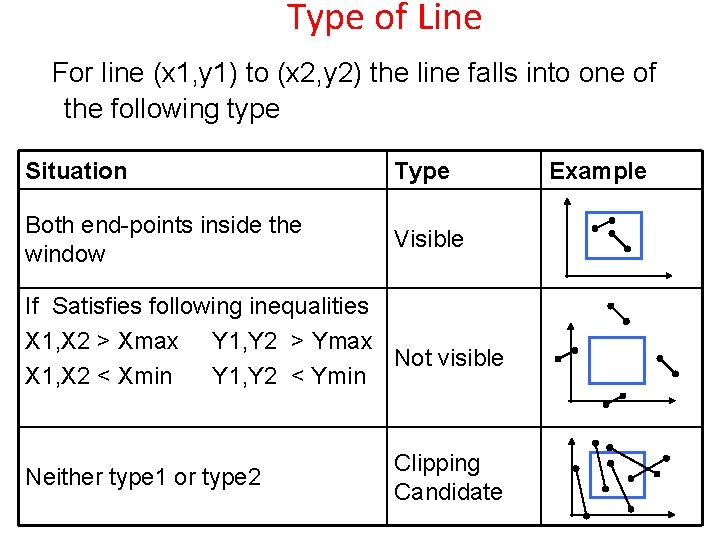
Type of Line For line (x 1, y 1) to (x 2, y 2) the line falls into one of the following type Situation Type Both end-points inside the window Visible If Satisfies following inequalities X 1, X 2 > Xmax Y 1, Y 2 > Ymax Not visible X 1, X 2 < Xmin Y 1, Y 2 < Ymin Neither type 1 or type 2 Clipping Candidate Example

Cohen-Sutherland Clipping Algorithm • An efficient line clipping algorithm • Advantage - it vastly reduces the number of line intersections that must be calculated Cohen is something of a mystery – can anybody find out who he was? Dr. Ivan E. Sutherland codeveloped the Cohen. Sutherland clipping algorithm. Sutherland is a graphics giant and includes amongst his achievements the invention of the head mounted display.

Steps Of Cohen-Sutherland algo STEPS : 1. Identify the line to be clipped a) Assign 4 bit code to end points of each line b) Categories each line 2. Perform the clipping : Using the slope intercept method or Mid point sub division method

Identify the line to be clipped • World space is divided into regions based on the window boundaries – Each region has a unique four bit region code – Region codes indicate the position of the regions with respect to the window 1001 3 2 1 above below right Region Code Legend 0 left 0001 0101 1000 0000 Window 0100 1010 0110

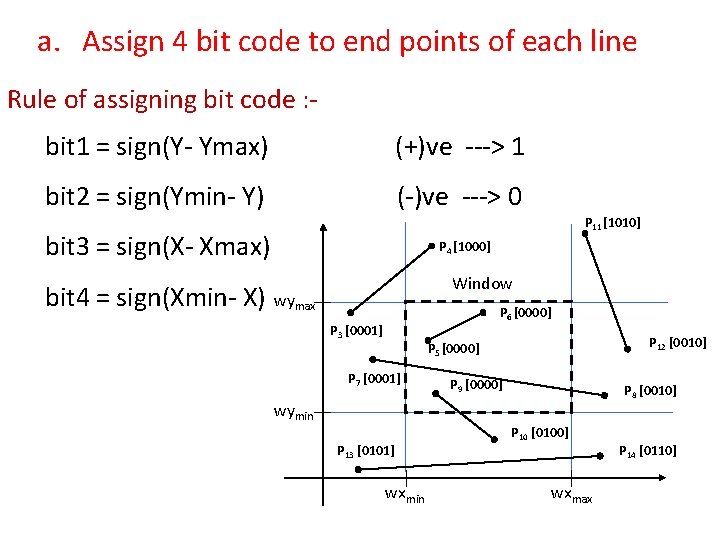
a. Assign 4 bit code to end points of each line Rule of assigning bit code : bit 1 = sign(Y- Ymax) (+)ve ---> 1 bit 2 = sign(Ymin- Y) (-)ve ---> 0 P 11 [1010] bit 3 = sign(X- Xmax) P 4 [1000] Window bit 4 = sign(Xmin- X) wymax P 6 [0000] P 3 [0001] P 12 [0010] P 5 [0000] P 7 [0001] wymin P 13 [0101] wxmin P 9 [0000] P 8 [0010] P 10 [0100] wxmax P 14 [0110]

b. Categories all the Lines if both end pt code is 0000 bit wise OR is all o’s • Not Visible If logical AND of end pt code is not 0000 • Clipping Candidate - If logical AND of end pt code is 0000 • Visible - P 11 [1010] P 4 [1000] Window wymax P 6 [0000] P 3 [0001] P 12 [0010] P 5 [0000] P 7 [0001] P 9 [0000] wymin P 13 [0101] wxmin P 8 [0010] P 10 [0100] wxmax P 14 [0110]

Perform Clipping • Using slope Intercept Method Let line end pt is (X 1, Y 1) & (X 2, Y 2) It can intersect either Vertical / Horizontal boundary – Let vertical Boundary at (X, Y) Hence X = WXmax / WXmin Y = Y 1 + m * (X – X 1) where m = slope of line – Let Horizontal Boundary at (X, Y) Hence Y = WYmax / WYmin X = X 1 + (Y – Y 1)/ m where m = slope of line

Exceptional Case P 4 [1000] P 4’ [1001] Window wymax P 3 [0001] wymin wxmax

Mid point sub-division method (Based on binary Search) • The line is divided at it’s mid point into 2 segment • the line type is found for those 2 segment – for type 1 (visible) – draw – for type 2 (Not Visible) – discard – for type 3 (clipping candidate) – apply the mid point sub-division Window wymax wymin wxmax

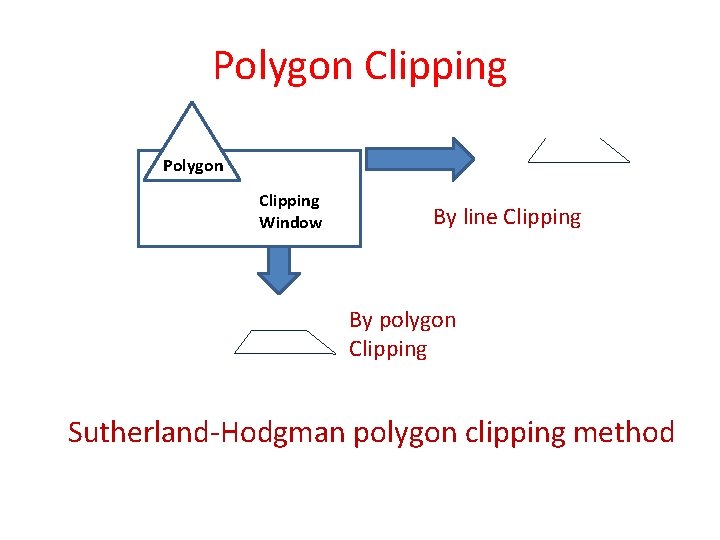
Polygon Clipping Window By line Clipping By polygon Clipping Sutherland-Hodgman polygon clipping method

Sutherland-Hodgman polygon clipping method • Clip the polygon by processing the polygon edge as a whole against each window edge • Beginning with initial vertex list Ø Clip the polygon w. r. t left boundary - Form new vertex list Ø Clip the polygon w. r. t right boundary - Form new vertex list Ø Clip the polygon w. r. t buttom boundary - Form new vertex list Ø Clip the polygon w. r. t top boundary - Form new vertex list

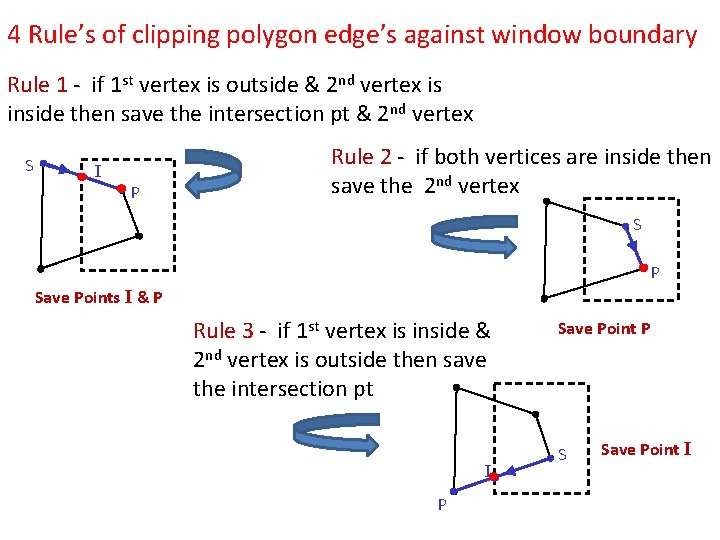
4 Rule’s of clipping polygon edge’s against window boundary Rule 1 - if 1 st vertex is outside & 2 nd vertex is inside then save the intersection pt & 2 nd vertex S I P Rule 2 - if both vertices are inside then save the 2 nd vertex S P Save Points I & P Rule 3 - if 1 st vertex is inside & 2 nd vertex is outside then save the intersection pt I P Save Point P S Save Point I

Rule 4 - if both vertices are outside then don’t save any vertex P Hence the clipped polygon is S No Points Saved e. g of clipped polygon