Tutorial on Widening and Narrowing Hongseok Yang Seoul

Tutorial on Widening (and Narrowing) Hongseok Yang Seoul National University

Goal of Abstract Interpretation int P() { int x = 2; while (x >= 0) { // Question: which value can “x” have here? x = x + 1; } return(x); } n An abstract interpretation answers this question by “executing” a program “abstractly”. n The answer is an upper approximation.

Usual Abstract Interpretation n n x = 2; while (x >= 0) {/* i 2 I */ x = x+1; } First, define a finite lattice <L, ? , t, u, >>. n Each element of L denotes a set of integers that “x” can have in the loop. Second, define a monotone function F: L ! L. n F is the abstraction of the loop body. Finally, compute the least fixpoint fix(F). 2 n fix(F) is the limit of ? , F(? ), F (? ), … n n Since L is finite and F (? ) is increasing, the sequence “terminates”. Example: L = {? , +, 0, -, >} and F(X) = (+ t (X © +))

Infinite Abstract Domain n n Question: Can we use an infinite lattice L? n Using a larger L, we can obtain a better estimate of a program invariant. n But, fix(F) might not be computable. Answer: Yes, we can, if we have widening. n Intuitively, widening works by picking a different finite subset of L for each program F.

Goal of this Talk n n My goal is to demystify widening and narrowing: 1. What are widening and narrowing? 2. How do they allow us to use an infinite lattice? 3. How to design widening and narrowing? 4. Are they really necessary? Can we just live with finite lattices, or lattices with no strictly increasing chain? I’ll mostly focus on widening.

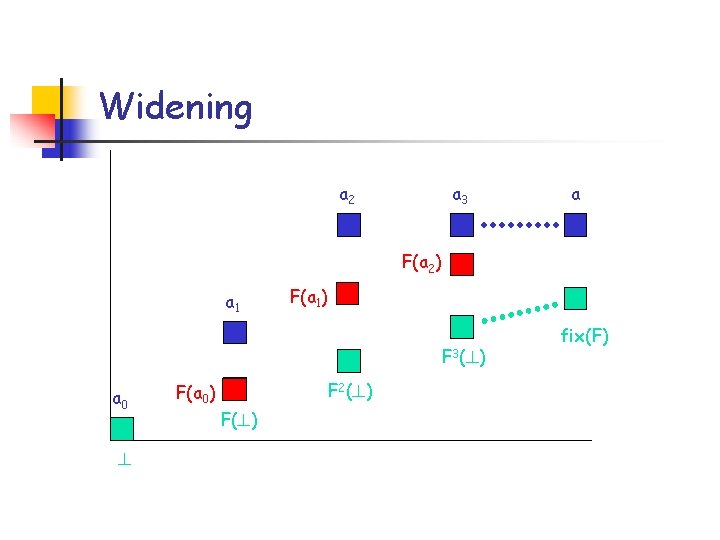
Problem Mathematically n n Question: Given an infinite lattice <L, ? , t, u, >> and monotone F: L!L, compute fix(F). n ? , F(? ), F 2(? ), … converges to fix(F). n But, the sequence might strictly increase. Widening approach asks a different question: Find an upper approximation “a” of fix(F), fix(F) v a. 1. First, approximate the sequence {Fn(? )} by a “terminating” sequence {an}: Fn(? ) v an. 2. Then, compute the limit “a” of {an}.

Widening “r: L£ L ! L” n n General Dfn: Widening is what gives us {an} for every F. n For every monotone function F, the below sequence {a n} approximates {Fn(? )} and terminates: a 0 = ? an+1 = an r F(an) Specific Dfn: Widening r : L £ L ! L is a function s. t. 1. x v x r y and y v x r y; and 2. for all increasing sequences {xn}n, the “widened” sequence yn terminates: y 0 = x 0 yn+1 = yn r xn+1

Widening a 2 a 3 a F(a 2) a 1 F(a 1) F 3(? ) a 0 ? F(a 0) F 2(? ) F(? ) fix(F)

Example n n Find fix(F) in the interval domain L: L = {? } [ {[l, u] | l, u 2 (Z [ {-inf, inf}) Æ l · u} F(X) = [0, 0] t (X + [1, 1]) Fn(? ) = [0, n-1]. Thus, {Fn(? )} is strictly increasing. Use the following widening r: [l, u] r ? = ? r [l, u] = [l, u] r [l’, u’] = [if l’ < l then -inf else l, if u’ > u then inf else u] What is the limit of {an}?

Technique for Designing Widening n n n For each non-bottom x ( != ? ), n decide a finite lattice Lx (µ L), and n define (xr-) as an “abstraction” fn from L to L x. (xr-) : L Lx : id Then, define ? rx = x. Example: for r in the previous slide, L[l, u] = {? , [l, u], [l, inf], [-inf, u], [-inf, inf]} This kind of widening lets us pick a different finite subset LF(? ) for each F. Exercise: F(X) = ([1, 1] t (X + [-1, 1])) u [-inf, 4]. Design a widening whose “a” for F is [-inf, 4].

Finite Domain on the Fly (My Observation) Suppose that for each non-bottom x ( != ? ), there is a subset Lx of L such that 1. Lx with the order of L is a lattice with finite height; 2. “ x : L Lx : id” is a Galois embedding; and x(x) = x = ? x. Proposition 1: If for all x and all y in Lx, Ly µ Lx, then “urw = u(w)” and “? rw = w” define a widening operator. Proposition 2: Moreover, if for all x and y in Lx, y(z) = x(z) tx y, then for every non-strict monotone function F, this widening picks LF(? ) in the computation: the n+1 -th term an+1 of the widened sequence is the n-th iterate of ( F(? ) o F): LF(? ) ! LF(? ). 3.

Widening Sequence {ri} n n n Is there a widening that uses Fk(? ) to decide a finite subset for F? n Need to use different “widening” ri for ai. For every monotone function F, the below sequence {a n} approximates {Fn(? )} and terminates: a 0 = ? an+1 = an rn F(an) A widening sequence {rn} is a sequence of fns s. t. 1. x v xrny and y v xrny; and 2. for all increasing sequences {xn}n, the “widened” sequence yn terminates: y 0 = x 0 yn+1 = ynrnxn+1 Design Technique: Usually, r 0=…=rk-1=t, and rk=rk+1=… Exercise: F(X) = ([1, 1] t (X + [-10, 10])) u [-inf, 30].

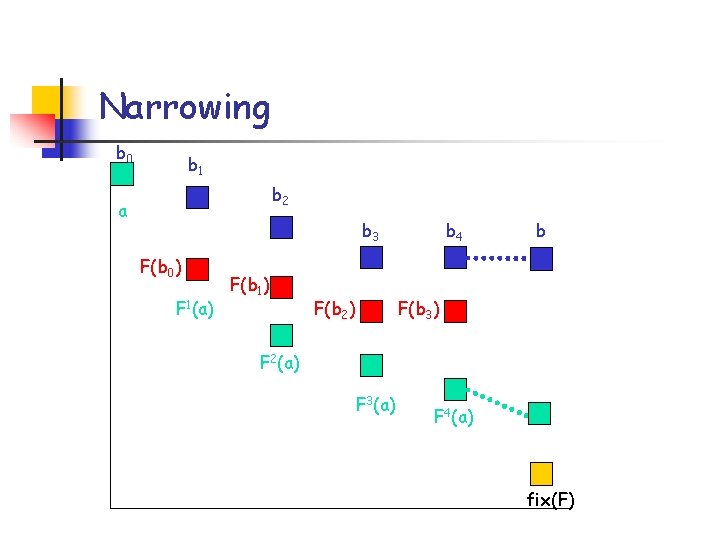
Increase the Precision n Problem: n Suppose we obtained an approximation “a” of fix(F) via widening. n From “a”, find a more precise approximation. Not-computable “solution”: n a, F(a), F 2(a), F 3(a), … n For each n, fix(F) v Fn(a) and Fn+1 v Fn(a). (* a w F(a)) Narrowing approach: 1. Approximate the sequence {Fn(a)} by a “terminating” decreasing sequence {bn}: Fn (a) v bn. 2. Then, b is the limit of {bn}.

Narrowing b 0 b 1 b 2 a b 3 F(b 0) F 1(a) F(b 1) F(b 2) b 4 b F(b 3) F 2(a) F 3(a) F 4(a) fix(F)

Narrowing n n General Dfn: Narrowing is what gives us {bn} for every F. n For every monotone function F, the below sequence {bn} approximates {Fn(a)}, is decreasing and terminates: b 0 = a bn+1 = bn r F(bn) Specific Dfn: Narrowing : L£ L ! L is a function such that 1. x w x y w y, and 2. for all decreasing sequences {xn}n, the “narrowed” sequence {yn} terminates: y 0 = x 0 yn+1 = yn xn+1

Widening/Narrowing Example n n F(X) = ([1, 1] t (X+[1, 1])) u [-inf, 100] Widening: n ? rx = xr? = ? n [l, u] r [l’, u’] = [if l > l’ then -inf else l, if u < u’ then inf else u] Narrowing: n ? x = x ? = ? n [l, u] [l’, u’] = [if l = -inf then l’ else l, if u = inf then u’ else u] Exercise: Compute an approximation of fix(F).

Finite Lattices Are Not as Powerful as Widening. int Pnm() { int i = n; while (i <= m) { // i 2 [n, m] i : = i + 1; } return(i); } n With a single “finite” abstract domain, we cannot find the invariant of “Pnm()” for all n and m. n {[n, m] | n · m} has a strictly increasing sequence. n We can find the invariant of all “Pnm()”s, using the interval domain and the widening and narrowing in the previous slide.

Conclusion n Widening lets us use an infinite lattice in designing an abstract interpreter. n It picks a finite subset depending on an input program. A common technique for designing widening is to compute Fk(? ) for some fixed k, and to use the result to build a finite subset. Why don’t you design an abstract interpreter based on an infinite lattice and widening?