Tuscan Squares Stoyan Kapralov ACCT2012 Pomorie 15 21













- Slides: 14

Tuscan Squares Stoyan Kapralov ACCT-2012 Pomorie, 15 -21 June 2012

The Idea GOLOMB’S PUZZLE COLUMNTM IEEE Information Theory Society Newsletter September 2010 2

The Beginning Solomon W. Golomb and Herbert Taylor, “Tuscan Squares – A New Family of Combinatorial Designs” Ars Combinatoria, 20 – B (1985), pp. 115– 132. 3

Applications IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 36. NO. 4, JULY 1990 A New Construction of Two-Dimensional Arrays with the Window Property J. DENES AND A. D. KEEDWELL Abstract - Tuscan squares, row-complete latin squares and commafree codes are used to construct binary and nonbinary arrays with a certain window property. Such arrays have practical applications in the coding and transmission of pictures. 4

Definitions - 1 An r x n Tuscan-k rectangle has r rows and n columns such that: (1) each row is a permutation of the n different symbols (2) for any two distinct symbols a and b, and for each m from 1 to k, there is at most one row in which b is m steps to the right of a. Tuscan square of order n: when r = n. 5

Definitions - 2 A Tuscan square is in standard form when the top row and the leftmost column contain the symbols in the natural order. A Roman square is both Tuscan and latin, and was originally called a row complete latin square. A Tuscan-(n-1) rectangle is a Florentine rectangle, and is a Vatican rectangle when it is also latin. 6

Examples - 1 12 21 1 2 3 4 2 4 1 3 3 1 4 2 4 3 2 1 1 2 3 4 5 6 2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 5 3 1 6 4 2 6 5 4 3 2 1 7

Examples -2 Tuscan but not Latin square 6 2 5 4 3 1 7 1 6 7 2 6 3 6 5 3 2 5 2 5 3 1 1 7 3 4 4 1 6 7 5 4 3 7 4 6 1 7 1 6 3 5 4 2 8

Examples - 3 A Tuscan-2 square of order 8 that is not Tuscan-3 1 2 3 4 5 6 7 8 2 1 8 1 4 2 3 6 7 7 1 5 2 5 4 8 1 5 4 2 8 7 5 7 8 3 7 4 5 6 6 3 4 8 2 8 1 4 7 5 6 6 6 3 3 3 8 4 5 2 3 7 6 1 9

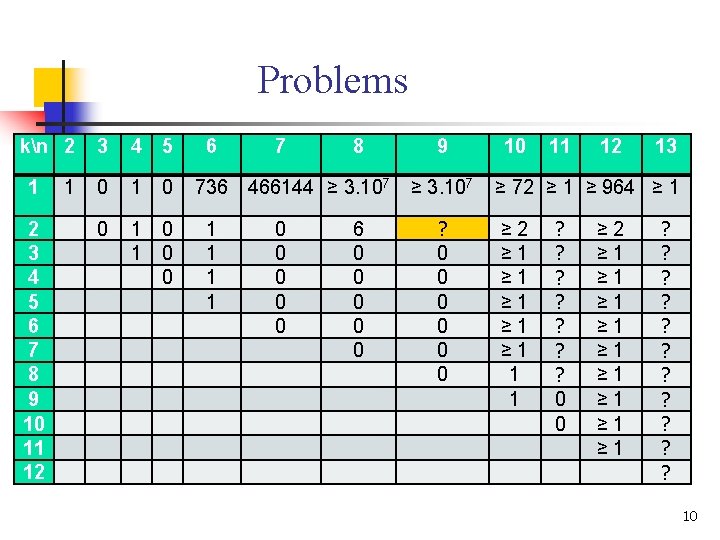
Problems kn 2 3 4 5 1 1 0 2 3 4 5 6 7 8 9 10 11 12 0 1 0 0 6 7 8 736 466144 ≥ 3. 107 1 1 0 0 0 6 0 0 0 9 ≥ 3. 107 ? 0 0 0 10 11 12 13 ≥ 72 ≥ 1 ≥ 964 ≥ 1 ≥ 2 ≥ 1 ≥ 1 ≥ 1 1 1 ? ? ? ? 0 0 ≥ 2 ≥ 1 ≥ 1 ≥ 1 ? ? ? 10

Our problem If there exists a Tuscan-2 square of order 9 ? 11

Plan of attack n n Reduce the task to the problem for searching cliques in graph. Using the Cliquer program of Patric Ostergard for searching the cliques. 12

Realization n Graph preparation n Number of vertices: 56 459 Number of edges: 203 140 075 n We are searching for a clique of size 8. n 13

The Result There is no Tuscan-2 square of order 9 14
 Tuscan plains
Tuscan plains Stoyan kenderov
Stoyan kenderov Acct2012
Acct2012 Damien thiesson
Damien thiesson Youcubed squares and more squares answers
Youcubed squares and more squares answers Wbc on hemocytometer
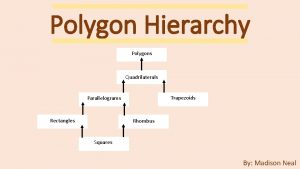
Wbc on hemocytometer Parallelogram hierarchy
Parallelogram hierarchy Pythagorean theorem perfect squares
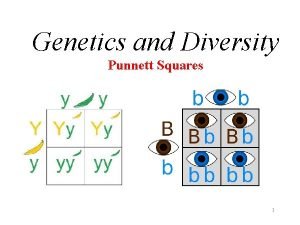
Pythagorean theorem perfect squares Heterozygous brown eyes
Heterozygous brown eyes Properties of rhombuses, rectangles, and squares
Properties of rhombuses, rectangles, and squares Broken squares activity template
Broken squares activity template Every rectangle is a parallelogram
Every rectangle is a parallelogram Cubed root of 1296
Cubed root of 1296 How to multiply radicals with coefficients
How to multiply radicals with coefficients Simplifying radical expressions
Simplifying radical expressions