Turning Forces Turning Forces You know that forces

Turning Forces

Turning Forces • You know that forces are a push or pull • A turning force is another force you come across in everyday life • Opening a Coke can, turning a door handle, or a tap, using a tin opener

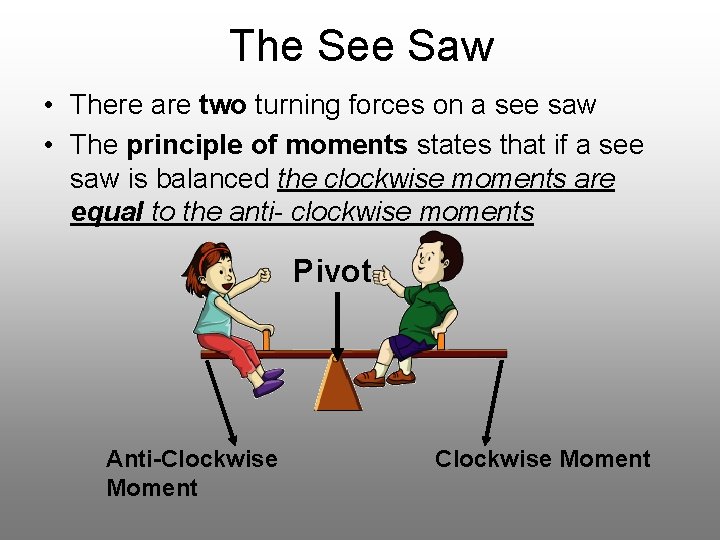
The See Saw • There are two turning forces on a see saw • The principle of moments states that if a see saw is balanced the clockwise moments are equal to the anti- clockwise moments Pivot Anti-Clockwise Moment

Turning Forces • Turning Forces are called Moments • To work out a moment you use Force (N) x Distance from the Pivot (m) • The units for moments are Newton metres (N m) • Moments can turn clockwise or anticlockwise

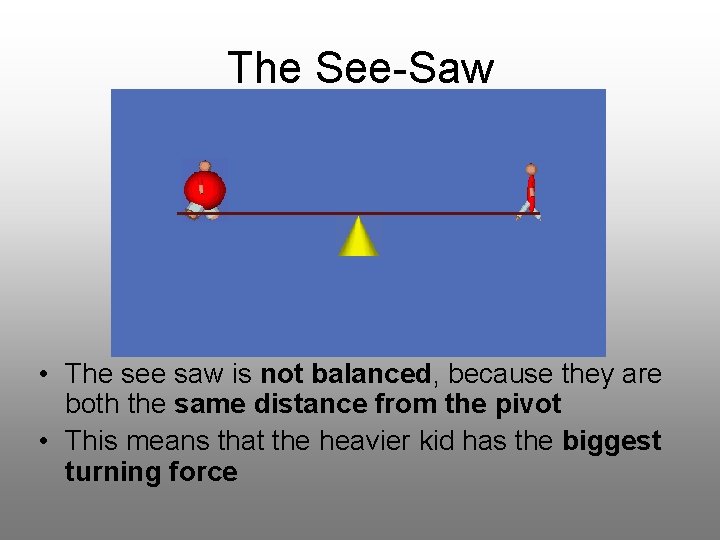
The See-Saw • The see saw is not balanced, because they are both the same distance from the pivot • This means that the heavier kid has the biggest turning force

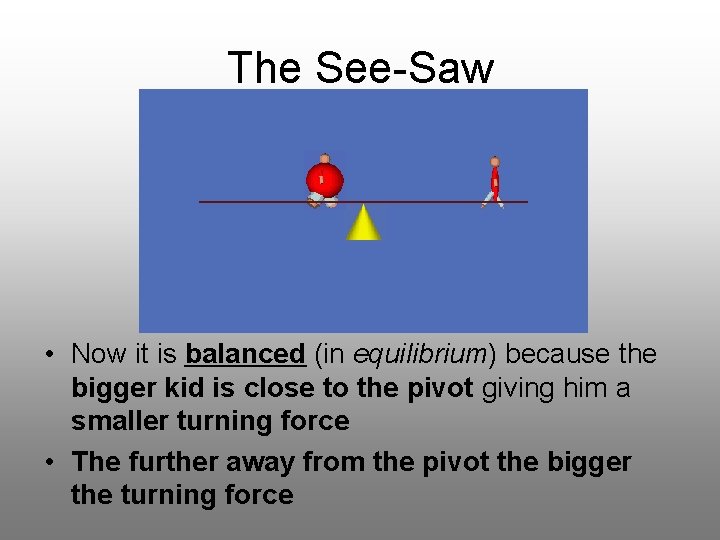
The See-Saw • Now it is balanced (in equilibrium) because the bigger kid is close to the pivot giving him a smaller turning force • The further away from the pivot the bigger the turning force

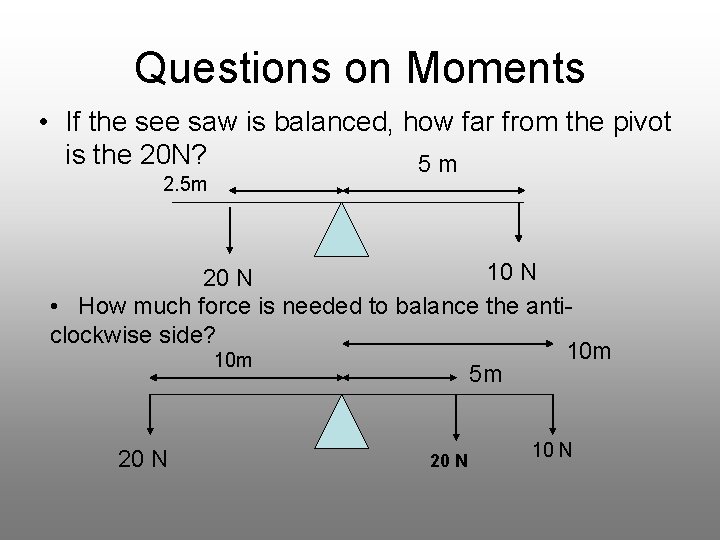
Questions on Moments • If the see saw is balanced, how far from the pivot is the 20 N? 5 m 2. 5 m 10 N 20 N • How much force is needed to balance the anticlockwise side? 10 m 5 m 20 N 10 N

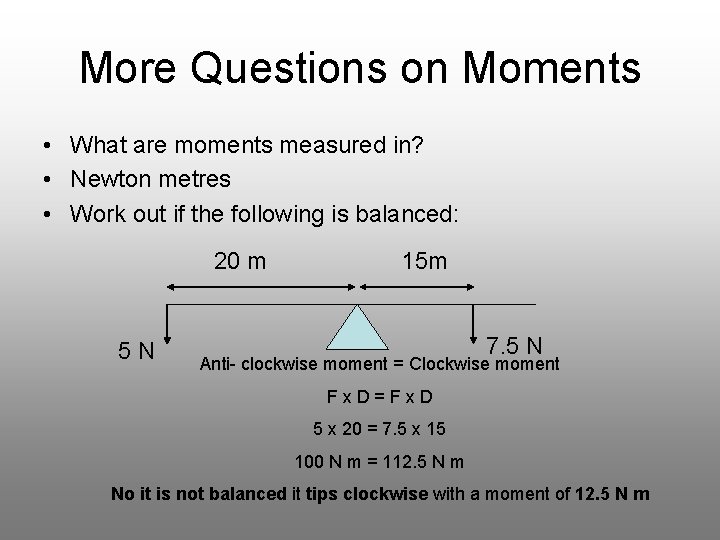
More Questions on Moments • What are moments measured in? • Newton metres • Work out if the following is balanced: 20 m 5 N 15 m 7. 5 N Anti- clockwise moment = Clockwise moment Fx. D=Fx. D 5 x 20 = 7. 5 x 15 100 N m = 112. 5 N m No it is not balanced it tips clockwise with a moment of 12. 5 N m

Levers • If you wanted to open this tin you would use a lever This screwdriver is too small to open the lid This crowbar is bigger so it can multiply the force you exert • It makes work easier

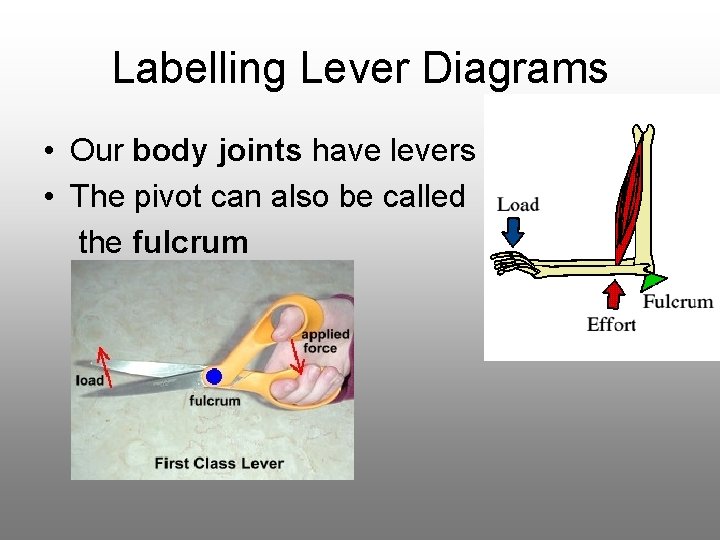
Labelling Lever Diagrams • Our body joints have levers • The pivot can also be called the fulcrum

The Wheelbarrow • This wheelbarrow can lift more than we can • The lever from the handles to the fulcrum multiplies our effort

Questions on Levers • What is the other name for the pivot? • The fulcrum • Look at the nutcracker, where is the pivot, load and effort Load Pivot Effort Load Effort

Stability • Stable objects are difficult to knock over Formula 1 cars have a low centre of gravity so that they don’t topple over Maradona had a low centre of gravity allowing him to turn quickly

Making something stable Give it a wide base

How to make things stable Give it a low centre of gravity

Unstable objects The tightrope walker needs the pole to lower his centre of gravity The unicyclist has a high centre of gravity Ice Skates have a narrow base

Questions on Stability • Sort these shapes according to their stability starting with the most stable • In each of the following diagrams the arrow is the centre of gravity, will these shapes fall over?

Links • http: //www. skoool. ie/skoool/junior. asp? id=3403 • http: //www. bbc. co. uk/schools/ks 3 bitesize/scienc e/physics/forces_motion_9. shtml