Turing Machines Part Two Common TMs CSCI 432

Turing Machines Part Two - Common TMs CSCI 432 Computer Science Theory

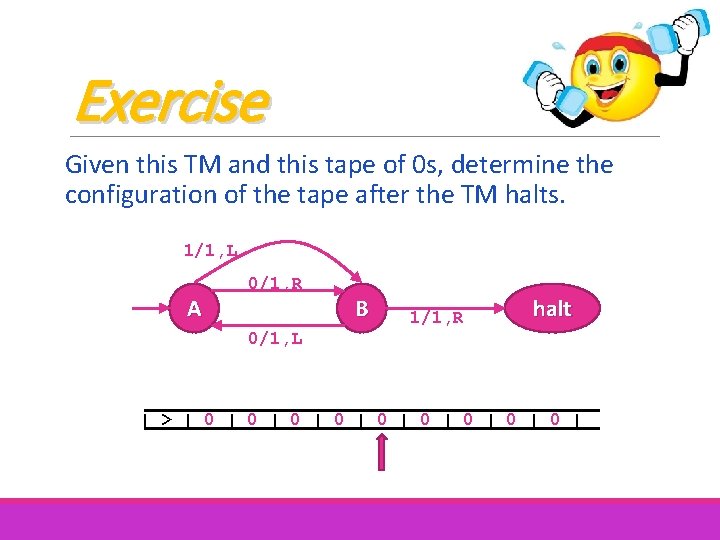
Exercise Given this TM and this tape of 0 s, determine the configuration of the tape after the TM halts. 1/1, L A 0/1, R B 1/1, R halt 0/1, L | > | 0 | 0 | 0 |

Busy Beaver Problem The previous TM is an example of a 2 -State "Busy Beaver" Turing Machine. Given an n-state TM with ∑ = {0, 1}, what is the max number of 1 s the machine can print on a tape of 0 s and still halt? S(1) S(2) S(3) S(4) S(5) S(6) proven max is 1 proven max is 4 proven max is 6 proven max is 13 theoretical max is 4098 may never be known, but is approximately 4. 6 x 101439 photo: jeremykun. com

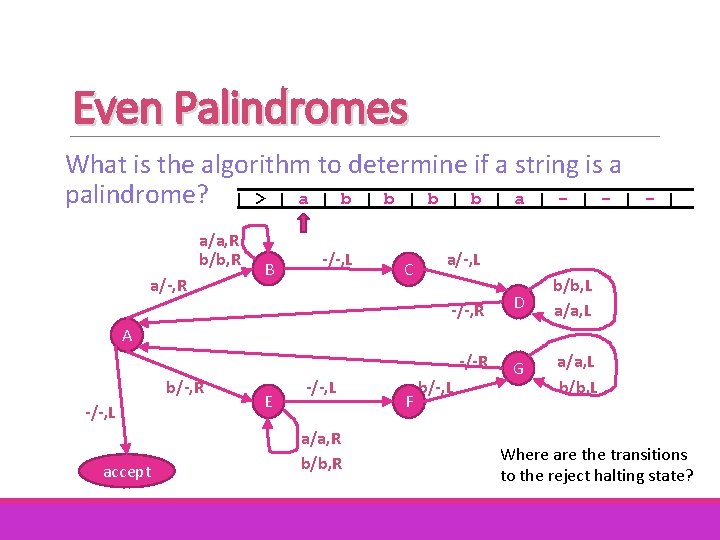
Even Palindromes What is the algorithm to determine if a string is a palindrome? | > | a | b | b | a | - | a/a, R b/b, R a/-, R B -/-, L C - | a/-, L -/-, R D b/b, L a/a, L -/-R G a/a, L b/b, L A b/-, R -/-, L accept E -/-, L a/a, R b/b, R F b/-, L Where are the transitions to the reject halting state?

Increment algorithm 10 + 1 = 11 11 + 1 = 100 1011 + 1 = 1100 + 1 = 1101 Non-TM Algorithm: go to far right (least significant digit) repeat if 0 or blank, write 1 and halt if 1, write 0 and go left

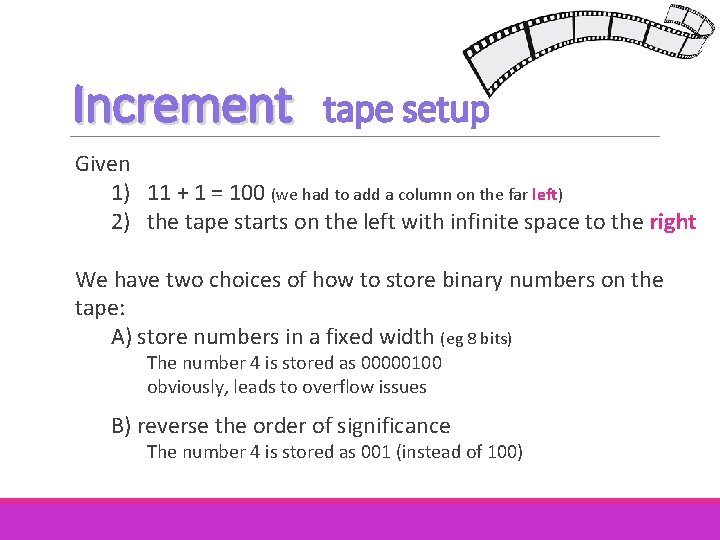
Increment tape setup Given 1) 11 + 1 = 100 (we had to add a column on the far left) 2) the tape starts on the left with infinite space to the right We have two choices of how to store binary numbers on the tape: A) store numbers in a fixed width (eg 8 bits) The number 4 is stored as 00000100 obviously, leads to overflow issues B) reverse the order of significance The number 4 is stored as 001 (instead of 100)

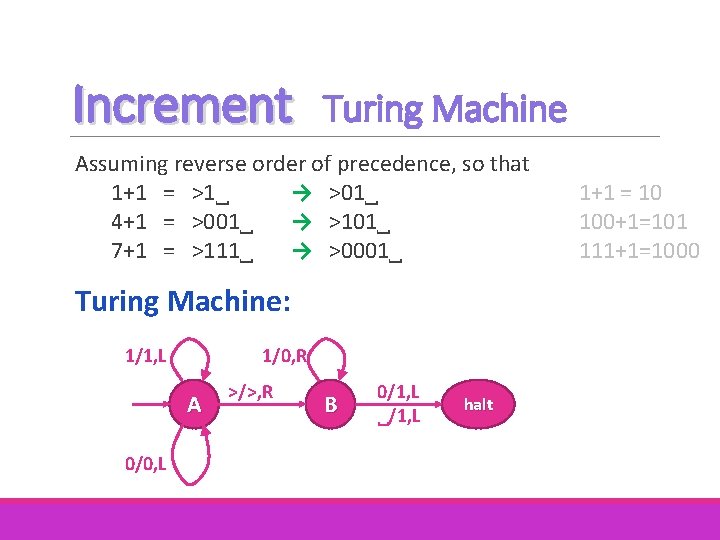
Increment Turing Machine Assuming reverse order of precedence, so that 1+1 = >1˽ → >01˽ 4+1 = >001˽ → >101˽ 7+1 = >111˽ → >0001˽ Turing Machine: 1/1, L 1/0, R A 0/0, L >/>, R B 0/1, L ˽/1, L halt 1+1 = 10 100+1=101 111+1=1000

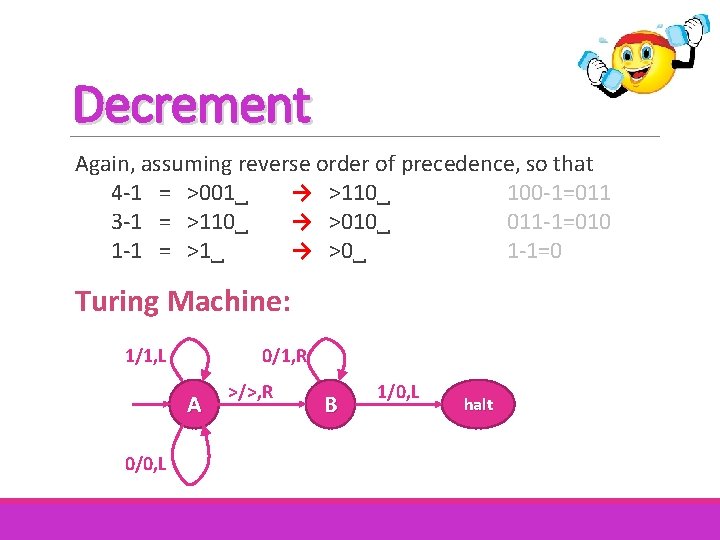
Decrement Again, assuming reverse order of precedence, so that 4 -1 = >001˽ → >110˽ 100 -1=011 3 -1 = >110˽ → >010˽ 011 -1=010 1 -1 = >1˽ → >0˽ 1 -1=0 Turing Machine: 1/1, L 0/1, R A 0/0, L >/>, R B 1/0, L halt

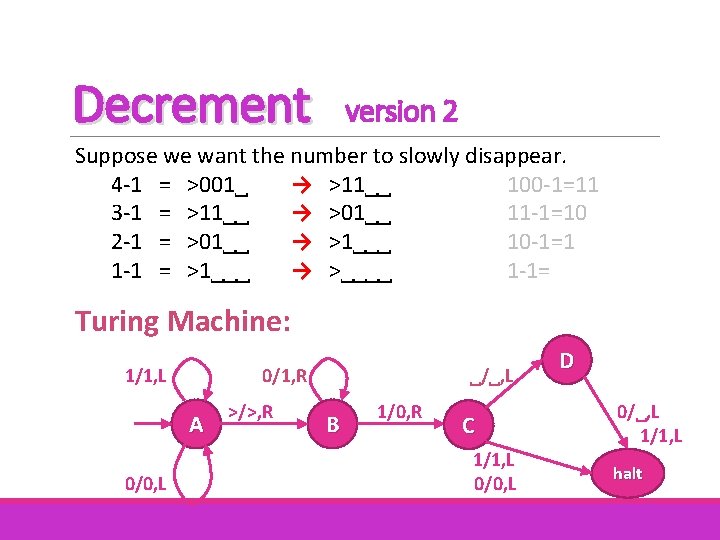
Decrement version 2 Suppose we want the number to slowly disappear. 4 -1 = >001˽ → >11˽˽ 100 -1=11 3 -1 = >11˽˽ → >01˽˽ 11 -1=10 2 -1 = >01˽˽ → >1˽˽˽ 10 -1=1 1 -1 = >1˽˽˽ → >˽˽˽˽ 1 -1= Turing Machine: 1/1, L 0/1, R A 0/0, L >/>, R ˽/˽, L B 1/0, R C 1/1, L 0/0, L D 0/˽, L 1/1, L halt

Addition Given our previous TMs that increment and decrement, and the tape configuration >A#B#˽ How would we create a TM to add A and B? For example, A=2 and B=3 | > | A | 0 | 1 | B | 1 | - | - |